1)Сте́пени свобо́ды — характеристики движения механической системы. Число степеней свободы определяет минимальное количество независимых переменных (обобщённых координат), необходимых для полного описания движения механической системы. Также число степеней свободы равно полному числу независимых уравнений, полностью описывающих динамику системы.

Подавляющее большинство физических систем может находиться не в одном, а во многих состояниях, описываемых как непрерывными (например, координаты тела), так и дискретными (например, квантовые числа электрона в атоме) переменными. Независимые «направления», переменные, характеризующие состояния системы, называются степенями свободы.

2)Число степеней свободы - наименьшее количество параметров которые необходимо задать чтобы однозначно определить положение тела в пространстве. обозначается i.
минимальное значение которое может принять i это 3.
т.к. три координаты х,y,z. Это значит что Материальная точка движется только поступательно.
Но если тело, или молекула вращается то каждому вращательному движению приписывается ещё одна степень свободы.
В случае двухатомного газа i=5.
т.к. его молекула может вращаться в двух перпендикулярных плоскостях.
В случае трёхатомного газа i=6.
т.к. его молекула способна вращаться в трёх взаимно-перпендикулярных плоскостях.
При увеличении температуры, атомы в молекулах начинают колебаться. Каждому колебательному движению приписывают две степени свободы. Одна соответствует кинетической энергии, другая потенциальной энергии взаимодействия. По этому с увеличением температуры увеличивается число степеней свободы для 2-х и более -атомных молекул.

M - произвольная масса газа.
N - про-ное кол-во частиц.
Внутренняя энергия одной молекулы

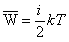
средняя кинетическая энергия поступательного движения молекулы равна

.

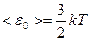Поскольку каждая молекула всегда обладает тремя степенями свободы поступательного движения и не одна из этих степеней не имеет преимущества перед другими, на каждую степень свободы поступательного движения приходится энергия, равная

.

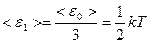Т.к. движение молекул является хаотическим, то любое движение – поступательное и вращательное - является равновероятным. Из этого предположения следует один из важнейших законов статистической физики – закон Больцмана о равномерном распределении энергии по степеням свободы молекул: на каждую степень свободы поступательного и вращательного движения молекулы приходится в среднем одинаковая кинетическая энергия, равная .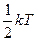

Для реальных молекул на каждую колебательную степень свободы приходится как кинетическая, так и потенциальная энергия.

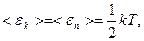поэтому .

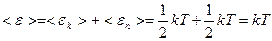Таким образом, средняя кинетическая энергия молекулы

,

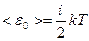где i – число степеней свободы молекулы.