Для грамотного и осмысленного применения линейной геостатистики необходимо уметь делать четыре основные математические операции:

уметь вычислять среднее и дисперсию случайных величин (и позже - пространственных переменных),

уметь использовать элементы теории множеств, т.е. записывать операции одинарного и двойного суммирования, а не длинные списки переменных,

уметь дифференцировать для нахождения минимума функции, и

быть знакомым с матричной записью для записи систем линейных уравнений.

Так как третья и четвертая темы привычны для математики, то читатель не будет иметь проблемы с поиском соответствующей литературы. Поэтому мы сделаем обзор только первых двух тем.

А 1.1 Среднее и дисперсия

В геостатистике мы используем линейные комбинации (т.е. взвешенное движущееся среднее) данных для оценивания величин переменных в точках или средних значений блоков. Например, типичная линейная комбинация –

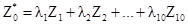
Кригинг оптимизирует выбор весов минимизации дисперсии оценивания. Поэтому нам нужно уметь выражать дисперсию через функцию от весов, l₁, l₂, …, l₁₀, и позже - через модели вариограмм. Для начала необходимо знать среднее и дисперсию линейной комбинации:

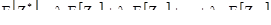
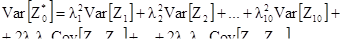
Этот результат хорошо известен в математике. Доказательство можно найти в литературе по статистике. Отсюда мы можем перейти к вычислению среднего и дисперсии ошибки оценивания. Если нашей целью является использование приведенной выше линейной комбинации для оценивания значения переменной в точке x₀, то ошибка оценивания :

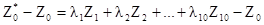
Это выражение - предыдущая линейная комбинация с дополнительным слагаемым (с весом равным -1). Поэтому ее среднее и дисперсия:

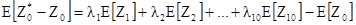
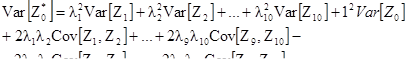
В Главах 2 и 3 показано, как оценивать эти дисперсии для пространственных переменных (но не сами случайные переменные), используя вариограммы или пространственные ковариации для учета их расположения в пространстве. Далее в Главе 7 показано, как минимизировать их дисперсии.

А 1.2 Одинарное и двойное суммирование

Уравнения для вычисления математического ожидания (среднего) и дисперсии длинные и громоздкие. Будет разумнее использовать короткую запись без выписывания всех слагаемых. Операция суммирования предназначена как раз для этого. Для обозначения этой операции используется греческая буква S (произносится сигма). Используя это обозначение, можно записать формулу математического ожидания, как одинарное суммирование:

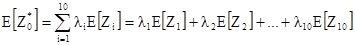
Аналогично можно записать выражение для дисперсии

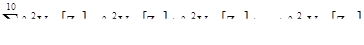
В заключении нам необходима формула дисперсии в терминах ковариаций. Так как каждое слагаемое содержит два индекса, то требуется двойное суммирование по двум переменным:

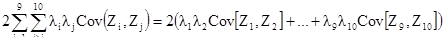
С двойным суммированием требуется больше осторожности. Несколько упражнений на одинарное и двойное суммирование позволят вам свободнее использовать их.

А 1.3 Упражнения на использование суммирования

Упр 1. Раскройте приведенные ниже формулы суммирования:

, , , ,

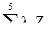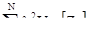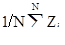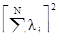Упр 2. Раскройте следующие формулы двойного суммирования:

, ,

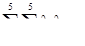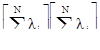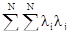
Упр 3. Покажите, что:

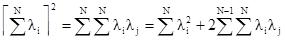
Упр 4. Покажите, что:

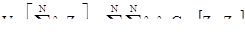
Приложение 2: Заключительные советы