Представленный выше метод используется, когда пробы равномерно распространены в пространстве. Он не используется, если данные в одном направлении намного гуще, чем в другом, как, например, происходит в сейсмической разведке, гидролокационном обнаружении скоплений рыб или (иногда) в подземном опробовании месторождений. Когда данные близко расположены вдоль линий с большим расстоянием между ними, для вычисления дисперсии оценивания должен использоваться другой метод аппроксимации. Он включает в себя объединение ошибок, сделанных при экстраполяции содержаний проб вдоль линий, и, затем экстраполяцию линейных содержаний на пространство между линиями.

На Рис. 10.4 проиллюстрирован случай с двумя профилями. Область опробована вдоль двух профилей d₁ и d₂. Если расстояние между пробами вдоль линий профилей равно s, то на первой линии размещается n₁=d₁/s проб. Если имеется больше двух профилей, то расстояние между ними принимается постоянным. Сечения такой ширины изображаются с центром на линии профиля. В данном случае они обозначены v₁ и v₂. Поэтому вся область V представляет собой сумму отдельных сечений.

Пусть Z(V) будет действительным, но неизвестным содержанием всего объема V. Примем также, что Z(v_i) и Z(d_i) - действительные значения сечения v_i и линии d_i. Для начала мы предположим, что линии сечений проанализированы точно, поэтому мы точно знаем Z(d_i). Чтобы оценить Z(V), мы должны взвесить каждое Z(d_i) по его сечению v_i. Так как расстояние между профилями постоянно, то 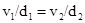 и мы имеем

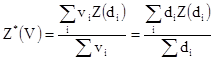                                                                                   [10.11]

Рис 10.4. Два профиля (разделения) длины d₁ и d₂

Аналогично действительное, но неизвестное значение Z(V) –

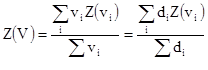                                                                  [10.12]

Поэтому ошибка оценивания – взвешенное среднее элементарных ошибок оценивания, что значит - Z(d_i)- Z(v_i):

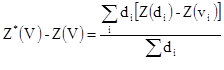                                                              [10.13]

По принципу аппроксимации дисперсия оценивания –

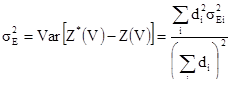                                                            [10.14]

где 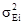 – элементарная дисперсия распространения центральной линии сечения на ее область влияния. Обратите внимание на то, что они взвешены с помощью квадратов длин d_i.

Более правдоподобно сечения линий вычисляются расчетом среднего содержания проб вдоль линии сечения. Так как пробы расположены на одинаковом расстоянии, то для оценивания Z*(d_i) используется среднее n_i проб:

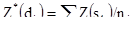                                                                                                              [10.15]

Общая ошибка оценивания Z*(V)-Z(V) может быть разделена на два слагаемых.

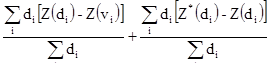                                                  [10.16]

Левое слагаемое соответствует распространению линии сечения на окружающее пространство, в то время как правое слагаемое соответствует распространению проб на линию сечения. Если мы положим, что Z(s_ik) и Z*(s_ik) являются действительными и оцененными содержаниями k-ой пробы в i-ой секции, то второе слагаемое можно переписать, как

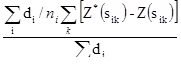                                                                               [10.17]

Как обычно, сумму ковариаций полагаем равной нулю, поэтому мы можем просуммировать дисперсии. В итоге получаем:

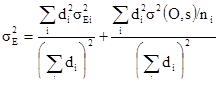                                       [10.18]

Если N обозначает общее количество проб ( 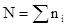) то

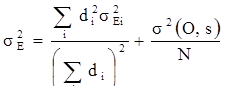                                     [10.19]

Поэтому общая дисперсия оценивания является композицией сечения, которая отвечает за распространение линии сечения на ее область, и композицией линии, 

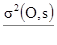                                                                               [10.20]

которая отвечает за ошибки, сделанные, когда пробы распространялись до линии сечения. Теперь мы опишем, как вычислять дисперсию оценивания, когда зона минерализации в целом не известна.