Раз мы знаем, как вычислить дисперсию оценивания, мы можем найти оптимальную сеть бурения для оценивания той или иной переменной. Здесь термин "оптимальная" означает сетку, которая дает требуемую дисперсию оценивания при наименьшем количестве скважин (проб), и поэтому имеет наименьшую стоимость. Для изотропного месторождения должна использоваться регулярная квадратная сетка. Когда присутствует анизотропия, отношения расстояний между пробами вдоль основных осей должно быть пропорционально отношению анизотропии.
Предположим, что мы хотим оценить среднюю мощность пласта и среднее содержание (здесь мы имеем в виду содержание серы в угле) на участке 4км на 4км. Для упрощения мы принимаем, что пласт простирается по всему участку и является изотропным. На участке возможно пробурить 16 скважин по 1км сетке или 64 скважины по сети 500 м, как показано на Рис. 10.7.

Рис 10.7. Две возможных сетки бурения
Предположим, что вариограмма мощности сферическая с зоной 1500м и порогом 1.0 , а вариограмма содержания серы также сферическая с зоной 200м и порогом 0.4.
Для 1км сетки
Дисперсию распространения можно найти, используя таблицы или небольшую компьютерную программу. В данном случае рассчитанные значения будут следующими:
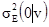 = 0.27 для мощности и
= 0.27 для мощности и
= 0.38 для содержания серы
Поэтому дисперсия оценивания:
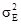 = 0.27/16=0.0169 для мощности и
= 0.27/16=0.0169 для мощности и
= 0.38/16=0.0238 для содержания серы
Для 500м сетки
Эти вычисления были повторены для 500м сетки:
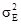 = 0.0020 для мощности и
= 0.0020 для мощности и
= 0.0055 для содержания серы
Чтобы сравнение между дисперсиями оценивания для двух переменных имело смысл, были вычислены коэффициенты вариации (т.е. СКО, разделенное на среднее, выраженное в процентах). Часто бывает полезным вычерчивание коэффициента вариации на одном графике (с би-логарифмической шкалой) с количеством скважин.
Чтобы получить грубую оценку точности, можно взять интервал, равный среднему 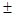 удвоенное СКО, что соответствует 95% доверительному интервалу. Для 1000м сетки значения мощности имеют точность
удвоенное СКО, что соответствует 95% доверительному интервалу. Для 1000м сетки значения мощности имеют точность 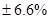 , тогда как содержания серы – только
, тогда как содержания серы – только 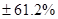 . Эти цифры отражают зоны влияния двух моделей вариограмм (1500м в сравнении с 300м). В результате, если даже эта сетка опробования оптимальна для мощности, то она не будет достаточно точной для содержания серы.
. Эти цифры отражают зоны влияния двух моделей вариограмм (1500м в сравнении с 300м). В результате, если даже эта сетка опробования оптимальна для мощности, то она не будет достаточно точной для содержания серы.
Табл. 10.6. Относительная точность для содержания серы и мощности пласта для двух возможных сеток бурения
| Сетка 1000 м | Сетка 500 м | |
| Мощность | 0,033 | 0,011 |
| Содержание серы | 0,309 | 0,148 |
Оптимальный эталон бурения зависит также от размера и (для маленьких размеров) от формы оцениваемого региона. Доминантным фактором, определяющим дисперсию оценивания, является общее количество скважин (проб), а не расстояние между ними. Поэтому, хотя 1000м сетка может быть оптимальной для одной переменной и определенной области, но она не будет достаточно плотной для района меньшего размера и будет излишне дорогой для большей области.
Когда границы рудного тела в начале разведки неизвестны, то лучше на этом этапе бурить скважины по достаточно широкой сетке и, затем, когда границы станут известными, заполнять их. В этом случае нельзя вначале определять дисперсию оценивания и оптимальное расположение, так как геометрическая ошибка зависит от размера и формы зоны минерализации.
Упражнения
Упр 10.1. Пятьдесят вертикальных скважин пробурено по регулярной сетке 200м на 200м с целью оценивания общих запасов угольного пласта в минерализованной зоне размерами 1000м на 2000м. Вариограмма для мощности пласта сферическая с зоной 500м и порогом 3.25. Какой принцип аппроксимации нужно использовать для вычисления общей дисперсии оценивания? Вычислите ее значение.
Вариограмма для содержания золы состоит из сферической структуры с зоной 250м и порогом 4.65 и эффектом самородка 1.35. Вычислите общую дисперсию оценивания для содержания золы.
Так как пробурено только 50 скважин, то, возможно, использовать кригинг. Вы можете пересчитать дисперсию оценивания для этого способа и сравнить со значениями, полученными принципами аппроксимации.
Упр 10.2. Восемьдесят скважин пробурено по регулярной сетке 200м на 200м для оценивания общих запасов месторождения рассыпного золота в минерализованной зоне с размерами 1600м на 2000м. Вариограмма для содержания золота – анизотропная сферическая модель с порогом 5. Анизотропия геометрическая с наибольшей зоной 500м в СЮ направлении и с наименьшей зоной 100м в ВЗ направлении. Какой принцип аппроксимации нужно использовать для вычисления общей дисперсии оценивания? Вычислите ее значение.
Упр 10.3. При сейсмической разведке квадратной области 4км на 4км интересующая нас переменная измерялась каждые 10м вдоль 4 профилей. Вычислите общую дисперсию оценивания, зная, что вариограмма является экспоненциальной моделью с зоной 500м и порогом 10.1 и эффектом самородка 3.9.
Упр 10.4. Горная компания проводит разведку для определения границ минерализации россыпного месторождения. Было пройдено 80 шурфов по регулярной сетке 50м на 50м (Рис. 10.8). Заштрихованная область обозначает блоки (шурфы) минерализованной зоны. Геологи в процессе разведки хотят вычислить дисперсию геометрической ошибки. Найдите значения N, N1 и N2, и затем вычислите дисперсию.
Обратите внимание, что этот рисунок почти такой же, как и Рисунок 10.6, за исключением отсутствия центральной пустой зоны. Сравните величину, вычисленную здесь для геометрической дисперсии, с величиной, вычисленной ранее.

Рис 10.8. Расположение разведочных шурфов (блоков минерализованной зоны).
Приложение 1: Обзор основных математических концепций
Дата: 2018-12-28, просмотров: 352.