Наблюдая, как веса и дисперсия кригинга изменяются при увеличении числа точек, мы получаем некоторое понимание о том, что размер окрестности кригинга может быть оптимальным. Опыт показал, что дисперсия кригинга является довольно нечувствительным параметром для проверки качества конфигурации кригинга. Вес среднего в простом кригинге и наклон линейной регрессии истинного значения и оценки оказываются гораздо более чувствительными параметрами контроля качества и, следовательно, более полезными. Теорема аддитивности в Главе 7 доказала, что оценку ОК можно записать как
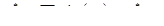 [8.8]
[8.8]
где m* - кригинговая оценка среднего, и что дисперсия ОК может быть представлена суммой дисперсии SK и выражением, зависящим от веса среднего в SK и дисперсии кригинга оценки среднего:
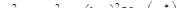 [8.9]
[8.9]
Первое уравнение показывает, что там, где вес среднего в простом кригинге lM мал (около 0), оценка в основном будет зависеть от локальных значений Z(x), т.е. от данных из конфигурации кригинга, а не от оценки m. Поэтому степень требуемой стационарности становится меньше. К тому же ОК оценка и SK оценка являются близкими друг к другу.
Второе уравнение показывает, что когда вес среднего в SK мал, то дисперсия OK близка к SK дисперсии. При этом слегка теряется точность при оценивании среднего. Наоборот, когда вес среднего в SK большой, то дисперсия OK становится больше чем дисперсия SK. Rivoirard (1984, 1987) показал, что уменьшение информации, доступной в окрестности кригинга, увеличивает важность среднего. Поэтому этот параметр показывает, как разброс данных связан с моделью вариограммы и также – какой уровень стационарности данных будет достаточным.
Дополнительные пробы улучшают качество оценки
На южно-африканском золотом руднике оценивались блоки 20м на 5м по бороздовым пробам по сети приблизительно 5м на 5м. В общем, обычно использовались ближайшие три линии проб. Иногда была доступна дополнительная линия проб по границе блока. Понятно, что использование этих дополнительных проб будет улучшать качество оценки, но на сколько? На Рисунке 8.11 показано два возможных расположения проб.
20m 20m
 |  |
5 m * * * * * 5m
* * * * * * * * * *
* * * * * * * * * *
* * * * * * * * * *
Рис 8.11. Два варианта расположения проб
Предположим, что вариограмма - сферическая с порогом 1.0 и зоной 20м. Дисперсия кригинга для первого варианта равна 0.368, а для второго - 0.114. Наклон линейной регрессии возрастает с 0.531 до 0.863, в то время как вес среднего в SK падает с 0.623 (достаточно высокий) до 0.255. Все три параметра качества показывают, что включение дополнительной строки проб приводит к значительному улучшению качества оценки.
Перекрестная проверка
Так как к экспериментальной вариограмме могут быть подогнаны несколько различных моделей вариограмм, то хорошо было бы знать, какая из них "лучшая". Часто для этого используется перекрестная проверка (кроссвалидейшн). Процедура состоит во временном удалении одной точки данных из исходного набора и оценки ее кригингом, используя оставшиеся пробы. Если эту операцию повторить для всех точек (или для созданного подмножества их) и для всех подобранных моделей вариограмм, то мы получим серию ошибок оценивания для каждой точки данных и для каждой модели вариограммы. Когда вариограмма подходит к данным, то среднее ошибок оценивания и среднее стандартизованных ошибок оценивания должны быть равны нулю, а дисперсия стандартизованных ошибок оценивания должна равняться 1.0.
Пусть 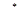 обозначает кригинговую оценку i-ой точки, вычисленной с использованием j-ой модели вариограммы, и пусть
обозначает кригинговую оценку i-ой точки, вычисленной с использованием j-ой модели вариограммы, и пусть 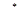 - дисперсия кригинга. Если действительное значение в точке - Zi, то соответствующая ошибка оценивания будет –
- дисперсия кригинга. Если действительное значение в точке - Zi, то соответствующая ошибка оценивания будет – 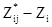 . Поэтому мы можем записать:
. Поэтому мы можем записать:
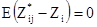 [8.10]
[8.10]
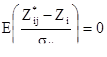 [8.11]
[8.11]
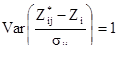 [8.12]
[8.12]
Это приводит нас к вычислению следующих статистик:
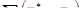 [8.13]
[8.13]
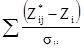 [8.14]
[8.14]
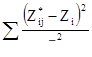 [8.15]
[8.15]
Так как любые крайние значения (т.е. выбросы) сильно действуют на все эти статистики, то было бы предпочтительно использовать их надежные (робастные) формы. Но не важно используются ли надежные или ординарные статистики, потому, что все три статистики никогда не показажут одну и ту же модель, как "лучшую". Поэтому должен быть сделан выбор.
Существуют практические проблемы в использовании этой методологии с данными бурения, потому что, когда выбирается и оценивается проба, то результат кригинговой оценки зависит в основном от ближайших проб (т.е. тех, которые выше и ниже по вертикали). Поэтому данная перекрестная проверка проверяет только, насколько хорошо подогнан вертикальный компонент вариограммной модели, а не вся оставшаяся модель.
Примеры иcпользования кригинга
Содержание
Пример в Главе5 был посвящен структурному анализу месторождения железной руды. Здесь мы покажем, как использовать подогнанную трехмерную модель вариограммы для кригинга значений точек, а затем - содержаний блоков. Так как модель имеет большой эффект самородка, то требуется большая окрестность кригинга. Четвертый параграф покажет, что произойдет, если использовать малую окрестность. Последний параграф проиллюстрирует, почему неэффективно оценивать кригингом маленькие блоки по данным разбросанных проб, а также рассчитывать извлекаемые запасы.
Месторождение железной руды
Данные, доступные для оценки этого месторождения, состоят из 500 проб длиной по 15м из 40 вертикальных скважин. Модель вариограммы состоит из эффекта самородка 1.8 и двух анизотропных сферических структур. Их пороги и зоны в горизонтальном и вертикальном направлениях представлены в Таблице 9.1.
В добывающей промышленности блочное оценивание является более распространенным, чем точечное оценивание, которое иногда используется в качестве исходной информации для оконтуривания. В этой главе мы проиллюстрируем использование обоих кригингов, точечного и блочного. При сравнении результатов, напомним о влиянии эффекта основания. Первый шаг в кригинге – это выбор размеров сетки.
Таблица 9.1. Параметры модели вариограммы, которая изотропна в горизонтальном направлении, но не в вертикальном
| Порог | Зона влияния по горизонтали | Зона влияния по вертикали | |
| Эффект самородка | 1.8 | - | - |
| 1-я структура | 1.2 | 80 м | 65 м |
| 2-я структура | 1.5 | 400 м | 65 м |
Размеры сети для кригинга
Так как расстояние между скважинами около 80м, то в горизонтальной плоскости сетка для кригинга будет иметь размеры 100м на 100м. Высота ячейки сетки будет 15м, потому что это длина секции керна. В итоге сетка состоит из 19 ячеек в направлении В – З, 12 ячеек в направлении С – Ю и из 36 вертикальных уровней. Не рекомендуется использовать кригинг для очень маленьких блоков (скажем 10м на 10м по горизонтали) или блоков, которые короче, чем длина секций керна (15м). Причины этого рассматриваются позже в этой главе.
Дата: 2018-12-28, просмотров: 350.