Выбор величены эффекта самородка крайне важен, так как он оказывает влияние на веса и дисперсию кригинга. Проблема при выборе эффекта самородка состоит в том, что часто нет никакой возможности узнать характер поведения вариограммы в начале, или, по крайней мере, для расстояний меньших, чем расстояние до первой точки на экспериментальной вариограмме. Если бурение дополнительных, близко расположенных скважин не доступно, то геостатистик должен спрогнозировать форму вариограммы около начала. Здесь важно понять, что выбор модели имеет большое влияние на результаты кригинга. Этот пример предназначен для иллюстрации влияния модели на веса кригинга и его дисперсию.



 2 * * * 2 * * *
2 * * * 2 * * *
1 1

 0 0
0 0
0 200 400 600 0 200 400 600
a b
Рис 8.4. Две возможные модели вариограммы с разным поведением в начале; (a) сферическая с зоной 200м, порогом 2.0 и (b) чистый эффект самородка 2.0
На Рис 8.4 показаны две возможные модели, подобранные к экспериментальной вариограмме, которая уже достигла порога в первой точке. Используя крайние случаи, ее можно смоделировать (I) сферический вариограммой с порогом 2.0 и зоной 200м (нулевой эффект самородка) или (2) чистым эффектом самородка с порогом 2.0. Если у нас нет каких-либо предшествующих знаний о переменной этого типа, то мы не можем обосновать, какую модель использовать: чистого эффекта самородка, модель с более сложной структурой или что-нибудь между ними.
*Z2

*Z3 *Z5 *Z1

*Z4
Рис 8.5. Блок 200м на 200м для оценки кригингом с помощью 5 проб
Предположим, что мы хотим оценить блок 200м на 200м, используя пробу в центре и 4 соседних пробы, расположенные по регулярной сетке 200м на 200м. (Примечание. Упражнение по кригингу из предыдущей главы имело такую же конфигурацию данных, но зона вариограммы была 250м, а не 200м).
Таблица 8.4. Веса и дисперсии кригинга для конфигурации из 5 точек
| Веса кригинга | Чистый эффект самородка | Сферическая |
| Центральная точка | 0.20 | 0.540 |
| Каждая внешняя точка | 0.20 | 0.115 |
| Дисперсия кригинга | 0.40 | 0.290 |
Веса и дисперсии кригинга показаны в Таблице 8.4. Разница между двумя дисперсиями кригинга очень значительная. Для чистого эффекта самородка она намного больше, чем для второй модели. Влияние типа модели на веса кригинга более тонкое. Модель эффекта самородка дает равный вес всем точкам и, следовательно, меньше центральной пробе и больше периферийным пробам, тогда как структурированная модель приписывает относительно высокий вес центральной пробе. Так как модель с низким эффектом самородка дает меньший вес центральной пробе, то это ведет к более существенному сглаживанию кригинговых оценок. Этот эффект будет проиллюстрирован в Главе 9.
Используемая здесь конфигурация из 5 точек нереалистично мала. На практике обычно выбирается гораздо большие окрестности с большим количеством проб. Интересно посмотреть, что произойдет, если увеличить количество проб. Следующий пример увеличит число точек до 9, расположенных также по регулярной сетке 200м на 200м. В Таблице 8.5 показаны веса кригинга и его дисперсии для этой новой конфигурации.
Таблица 8.5. Веса кригинга и дисперсия кригинга для конфигурации из 9 точек
| Веса кригинга | Чистый эффект самородка | Сферическая |
| Центральная точка | 0.11 | 0.51 |
| Внутренние точки | 0.11 | 0,08 |
| Внешние точки | 0.11 | 0.04 |
| Дисперсия кригинга | 0.22 | 0.26 |
Сравнивая результат с примером из 5 точек, мы видим, что увеличение окрестности приводит к изменению в весах и дисперсии кригинга для чистого эффекта самородка, но не для сферической модели. Как будет показано в следующем параграфе, пробы, близко расположенные к оцениваемой точке, эффективно экранируют влияние более отдаленных точек в случае, если вариограмма хорошо структурирована. Это утверждение не справедливо для плохо структурированных моделей с большим эффектом самородка или с короткой зоной влияния.
Экранный эффект
Программы опробования часто производят сотни или тысячи значений исходных данных. С вычислительной точки зрения имело бы здравый смысл препятствовать использованию всех их для оценивания каждого блока. Интуиция подсказывает, что оценки будут очень близки к реальным, если принимать в расчет только соседние данные. Проблема заключается в том, чтобы знать, сколько точек включить в расчет. Общее правило - брать только несколько первых ареалов (то есть колец) вокруг целевой точки, если вариограмма хорошо структурирована, то есть, если влияние эффекта самородка относительно маленькое. Причина в том, что несколько первых ареалов полностью экранируют влияние более отдаленных проб. Это можно лучше всего продемонстрировать на примере.
* * * * *
* * * * * * * *
 |  |
* * * * * * * *
 |  |
* * * * * * * *
а * * * * *
б
Рис 8.6. Блок с 1-м ареалом данных (a), и с 2-мя ареалами данных (b)
Предположим, что мы хотим оценить блок 200м на 200м с пробой в центре, используя данные, расположенные по сети 200м на 200м. Количество проб можно увеличивать с 1 (центральная проба), до 9 (1 ареал) и, затем до 25 (2 ареала). Когда модель вариограммы известна, веса и дисперсию кригинга можно вычислить для каждой конфигурации данных. Ясно, что каждое увеличение количества участвующих в оценке проб уменьшает дисперсию кригинга (или дисперсия остается той же самой). Чтобы проиллюстрировать, как работает экранный эффект, рассмотрим три случая: сферические вариограммы с порогом 2.0 и зонами 250м и 100 м соответственно, и чистый эффект самородка 2.0 (который можно представить как сферическую вариограмму с нулевой зоной). На Рисунке 8.7 изображены веса кригинга для конфигураций 9 и 25 точек для этех моделей вариограмм.
Для хорошо структурированной сферической модели (зона 250м, вверху рисунка) наибольшие веса сконцентрированы в центральной точке и четырех самых близких точках. Следовательно, увеличение количества точек больше 25, не ведет к какому-то существенному улучшению дисперсии кригинга. При этом величина оценки также не будет существенно изменяться, как и веса. Поэтому нам представляется, что в данном случае нет необходимости использовать больше данных, чем несколько ближайших точек. Когда вариограмма плохо структурирована (чистый эффект самородка или сферическая функция с короткой зоной), дисперсия кригинга с ростом проб продолжает понижаться, а веса для внешних точек не стремятся быстро к нулю. Поэтому в этой ситуации требуется большая окрестность кригинга. Пожалуйста, обратите внимание на то, что точки даже за пределами зоны вариограммы могут иметь отличные от нуля веса при использовании ОК. Они не обязательно равны нулю.
Сферическая модель, зона =250м,
Порог =2 0,8 0,8 0,5 0,8 0,8
2,6 8,2 2,6 0,8 1,2 7,0 1,2 0,8
 |  |
8,2 56,7 8,2 0,5 7,0 56,0 7,0 0,5
2,6 8,2 2,6 0,8 1,2 7,0 1,2 0,8
0,8 0,8 0,5 0,8 0,8
sк2 = 0,22 sк2 = 0,20
Сферическая модель, зона =100м,
Порог =2 3,3 3,3 3,3 3,3 3,3
9,4 9,4 9,4 3,3 3,3 3,3 3,3 3,3
 |  |
9,4 25,0 9,4 3,3 3,3 19,0 3,3 3,3
9,4 9,4 9,4 3,3 3,3 3,3 3,3 3,3
3,3 3,3 3,3 3,3 3,3
sк2 = 0,35 sк2 = 0,25
Чистый эффект самородка,
Порог =2 4,0 4,0 4,0 4,0 4,0
11,1 11,1 11,1 4,0 4,0 4,0 4,0 4,0
 |  |
11,1 11,1 11,1 4,0 4,0 4,0 4,0 4,0
11,1 11,1 11,1 4,0 4,0 4,0 4,0 4,0
4,0 4,0 4,0 4,0 4,0
sк2 = 0,22 sк2 = 0,08
Рис 8.7. Веса и дисперсия кригинга для конфигураций данных с одним или 2-мя ареалами для трех моделей вариограмм
Симметрия в уравнениях
Когда кригинг начинал развиваться, компьютерное оборудование было бедным. Обращение больших матриц для решения больших наборов линейных уравнений требовало очень много времени. Это стимулировало геостатистиков искать пути сокращения размера систем кригинга. Один из них - принимать во внимание симметрию системы. Например, данное в предыдущей главе упражнение рассматривало обычный кригинг блока, используя 5 точек данных, четыре из которых размещались симметрично вне блока. Для этих точек факторы взвешивания явно идентичны.
*Z2

*Z3 *Z1 *Z5
*Z4
Рис 8.8. Конфигурация с симметричными данными
Эти четыре пробы можно перегруппировать и рассматривать, как одну S с единственным фактором взвешивания. Каждая из исходных индивидуальных проб будет ее одной четвертью. Если первый вес связан с центральной точкой Z1, а второй вес с группой S, то систему кригинга можно переписать, как:
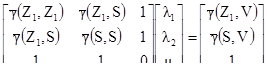 [8.1]
[8.1]
Поскольку не является очевидным, как вычислять различные вариограммные величины, то это будет представлено в подробностях.
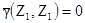 ,
, 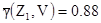 [8.2]
[8.2]
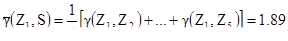 [8.3]
[8.3]
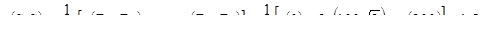 [8.4]
[8.4]
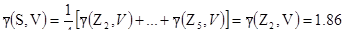 [8.5]
[8.5]
Это приводит к решению системы 3 на 3 вместо 6 на 6:
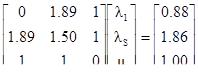 [8.6]
[8.6]
Решением является l1=0.60, lS=0.40 и m=0.12 и поэтому:
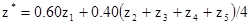 [8.7]
[8.7]
Конечно 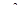 будет такая же, как и раньше. Здесь мы преуспели в сокращении системы от 6 на 6 до 3 на 3 без какой-либо потери точности. Так как время, необходимое для обращения матрицы, грубо пропорционально кубу размера системы, то уменьшая в два раза размер системы, мы эффективно уменьшаем время и, следовательно, стоимость вычислений на величину примерно равную одной восьмой от их первоначальных значений. Это конечно представляет значительную экономию.
будет такая же, как и раньше. Здесь мы преуспели в сокращении системы от 6 на 6 до 3 на 3 без какой-либо потери точности. Так как время, необходимое для обращения матрицы, грубо пропорционально кубу размера системы, то уменьшая в два раза размер системы, мы эффективно уменьшаем время и, следовательно, стоимость вычислений на величину примерно равную одной восьмой от их первоначальных значений. Это конечно представляет значительную экономию.
Понимая, что размер системы кригинга может быть значительно уменьшен (в некоторых случаях без потери точности), важно уметь отличать симметричную конфигурацию проб от тех случаев, которые только кажутся симметричными на первый взгляд. Чтобы иметь идентичные веса точки данных должны быть симметричными относительно друг друга и относительно оцениваемых точки или блока. В приведенной ниже конфигурации точки данных симметричны относительно друг друга, но не относительно блока.
*Z2

*Z3 *Z1 *Z5
*Z4
Рис 8.9. Конфигурация симметричных данных с удаленным блоком
Другой случай, который часто ведет к ошибкам, связан с ситуацией, когда данные и блок симметричны относительно друг друга, но модель вариограммы анизотропная.
Предположим, что конфигурация данных такая же, как на Рис. 8.10, но модель вариограммы имеет зону 500м в СЮ направлении и - 250м в ВЗ направлении. После соответствующей корректировки измерения в ВЗ направлении становятся в два раза больше измерений в СЮ направлении. В итоге веса для Z3 и Z5 идентичны, как и для Z2 и Z4, но они не равны как раньше. Это обстоятельство должно быть учтено при перегруппировке точек данных.
*Z2 *Z2
 |  |
*Z3 *Z1 *Z5 *Z3 *Z1 *Z5
*Z4 *Z4
Рис 8.10. Конфигурация проб до и после принятия во внимание анизотропии
Дата: 2018-12-28, просмотров: 452.