Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

● Сила и плотность электрического тока

, ,

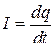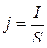где S – площадь поперечного сечения проводника.

● Плотность тока в проводнике

,

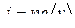где 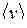- средняя скорость упорядоченного движения зарядов в проводнике (дрейфовая скорость); n – концентрация зарядов, е - заряд электрона.

● Электродвижущая сила, действующая в замкнутой цепи,

,

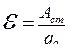где 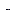- единичный положительный заряд; А_сm – работа сторонних сил.

● Сопротивление R однородного линейного проводника, проводимость G проводника и удельная электрическая проводимость 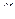 вещества проводника

,

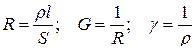где ρ – удельное электрическое сопротивление; S – площадь поперечного сечения проводника; - его длина.

● Сопротивление проводника при последовательном и параллельном соединении соответственно

,                                ,

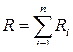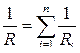где 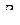- сопротивление i-го проводника; n – число проводников.

● Зависимость удельного сопротивления ρ от температуры

,

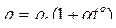где α- температурный коэффициент сопротивления; ρ₀ – удельное сопротивление при 0^о с.

● Закон Ома:

Для однородного участка цепи

;

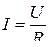для неоднородного участка цепи

;

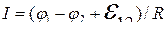для замкнутой цепи

,

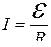где U – напряжение на участке цепи; R – сопротивление цепи (участка цепи), ( 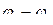) – разность потенциалов на концах участка цепи; ε₁₂- Э.Д.С. источников тока, входящих в участок; ε- Э.Д.С. всех источников тока цепи.

● Закон Ома в дифференциальной форме

,

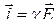где Е- напряженностью электростатического поля.

● Работа тока за время t

.

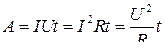● Мощность тока 

,

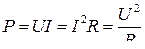● Закон Джоуля-Ленца

,

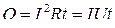где Q – количество теплоты, выделяющееся в участке цепи за время t.

● Закон Джоуля-Ленца в дифференциальной форме

,

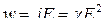uде 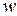- удельная тепловая мощность тока.

 

Магнитное поле

● Силовое действие магнитного поля на движущуюся заряженную частицу и проводник с током

,                        ,

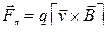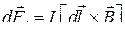где 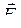 – сила, действующая на заряд q, движущийся в магнитном поле со скоростью 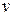,  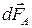– сила, действующая на элемент длины  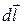проводника с током I, помещенный в магнитное поле с индукцией .

● Формула Лоренца

,

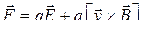где 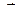 – результирующая сила, действующая на движущийся заряд q, если на него действуют электрическое поле напряженностью  и магнитное поле индукцией .

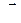● Связь магнитной индукции  и напряженности  магнитного поля

 ,

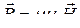где µ₀ = 4π∙10^-7 Гн/м – магнитная постоянная; µ - магнитная проницаемость среды.

● Закон Био – Савара – Лапласа

                                                         ,

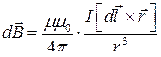 где 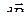– магнитная индукция поля, создаваемая элементом длины 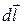проводника с током I;  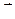– радиус-вектор, проведенный от dI к точке, в которой определяется магнитная индукция.

● Принцип суперпозиции (наложения) магнитных полей

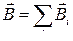
где  – магнитная индукция результирующего поля; 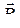 – магнитные индукции складываемых полей.

● Магнитная индукция поля, создаваемого бесконечно длинным прямым проводником с током,

,

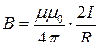где R – расстояние от оси проводника.

● Магнитная индукция в центре кругового проводника с током

,

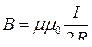где R – радиус кривизны проводника.

● Сила взаимодействия двух прямых бесконечных прямолинейных параллельных проводников с токами I₁ и I₂

 ,

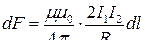 где R – расстояние между проводниками; dl – отрезок проводника.

● Магнитное поле точечного заряда q, свободно движущегося с нерелятивистской скоростью V,

,

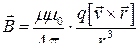где r – радиус-вектор, проведенный от заряда к точке наблюдения.

● Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора )

,

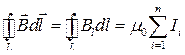где µ₀ – магнитная постоянная; 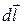 – вектор элементарной длины контура, направленной вдоль обхода контура;  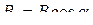– составляющая вектора  в направлении касательной контура L произвольной формы (с учетом выбранного направления обхода); α – угол между векторами  и ;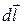   

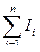 - алгебраическая сумма токов, охватываемых контуром.

● Магнитная индукция поля внутри соленоида (в вакууме), имеющего N

витков,

,

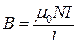где l  - длина соленоида.

● Магнитная индукция поля внутри тороида (в вакууме)

.

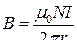● Механический момент, действующий на контур с током, помещенный в однородное магнитное поле,

,

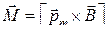где В – магнитная индукция; p_m – магнитный момент контура с током:

,

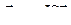где S – площадь контура с током; 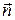 – единичный вектор нормали к поверхности контура.

● Энергия магнитного момента в магнитном поле

.

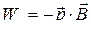● Поток вектора магнитной индукции (магнитный поток) через площадку dS

, 

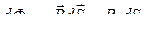где – вектор, модуль которого равен dS, а направление совпадает с нормалью 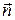 к площадке; B_n – проекция вектора  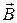на направление нормали к площадке.

● Поток вектора магнитной индукции сквозь произвольную поверхность S

.

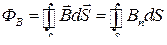● Работа по перемещению проводника с током в магнитном поле

dA = I d Φ,

где d Φ – магнитный поток, пересеченный движущимся проводником.

● Работа по перемещению замкнутого контура с током в магнитном поле

dA =I d Φ',

где d Φ' – изменение магнитного потока, сцепленного с контуром.

Электромагнитная индукция

● Закон электромагнитной индукции (Фарадея)

,

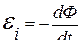где 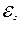  - э.д.с. индукции, возникающее в замкнутом контуре, при изменении магнитного потока, пересекающего поверхность этого контура.

● Потокосцепление

 ,

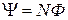где N – количество контуров (витков).

● Закон электромагнитной индукции (Фарадея) для произвольной системы проводников (катушка)

.

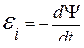● Магнитный поток, создаваемый током I  в контуре с индуктивностью L,

Φ = LI.

● Э.д.с. самоиндукции

,

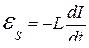где L – индуктивность контура.

● Индуктивность соленоида (тороида)

,

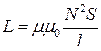где N число витков соленоида; l – его длина.

● Токи при размыкании и при замыкании цепи

;  ,

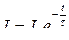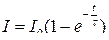где τ = L / R – время релаксации (L – индуктивность; R – сопротивление).

● Э.д.с. взаимной индукции (э.д.с., индуцируемая изменением силы тока

в соседнем контуре)

,

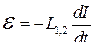где L₁₂ – взаимная индуктивность контуров.

● Взаимная индуктивность двух катушек (с числом витков N₁ и N₂), намотанных на общий тороидальный сердечник,

,

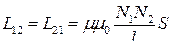где µ - магнитная проницаемость сердечника; l – длина сердечника по средней линии; S – площадь сердечника.

● Энергия магнитного поля, создаваемого током в замкнутом контуре

 

индуктивностью L, по которому течет ток I,

.

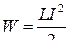● Объемная плотность энергии однородного магнитного поля

.

 

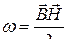Магнитные свойства вещества

● Связь орбитального магнитного 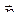 и орбитального механического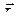

моментов электрона

,

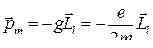где 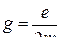– гиромагнитное отношение орбитальных моментов.

● Намагниченность

,

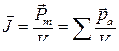где 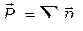 – магнитный момент магнетика, равный векторной сумме магнитных моментов отдельных молекул.

● Связь между намагниченностью и напряженностью магнитного поля

,

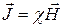где χ – магнитная восприимчивость вещества.

● Связь между векторами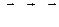

,

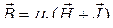где μ₀ – магнитная постоянная.

● Связь между магнитной проницаемостью и магнитной восприимчи-

востью вещества

μ = 1 + χ.

 

● Закон полного тока для магнитного поля в веществе (теорема о циркуляции вектора )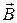

,

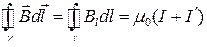где 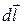 – вектор элементарной длины контура, направленный вдоль обхода контура; B_l – составляющая вектора  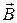в направлении касательной контура γ произвольной формы; I и I' – соответственно алгебраические суммы макротоков (токов проводимости) и микротоков (молекулярных токов), охватываемых заданным контуром.

● Теорема о циркуляции вектора напряженности магнитного поля

 ,

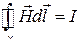где I – алгебраическая сумма токов проводимости, охватываемых контуром γ.

 

Примеры решения задач

Задача 1. Нить в форме полуокружности заряжена равномерно с линейной плотностью t. С помощью принципа суперпозиции найдите значение напряженности и потенциала в центре соответствующей окружности. 

 

Решение:

Рассмотрим элемент нити dl, несущий заряд dq=t × dl. К нему применимы формулы, определяющие поле точечного заряда, т.е.

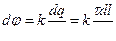 и .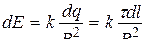

Т.к. каждый элемент в силу симметрии формы нити имеет симметричный участок (см. рисунок) вектор напряженности поля которого симметричен вектору 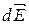 относительно указанной на рисунке оси симметрии, то суммарная напряженность поля будет направлена по оси симметрии и равна сумме проекций векторов  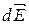на эту ось (проекции на перпендикулярное к этой оси направление взаимно компенсируются).

В соответствии с формулами 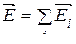,  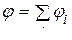получим значение потенциала поля нити:

.

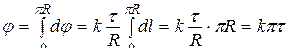Для нахождения напряженности потребуется взять в качестве переменной интегрирования не элемент длины, а элементарный угол d a:

,

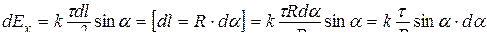тогда

.

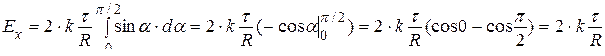Полученные значения относятся лишь к одному частному случаю (к единственной точке – центру).

Ответ: , .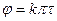

 

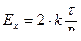Задача 2. Протон, движущийся со скоростью v₀=100 км/с, влетает в электрическое поле с напряженностью Е=50 В/м в направлении, противоположном направлению силовых линий поля. Какую разность потенциалов пройдет протон до полной остановки? Через сколько микросекунд скорость протона станет равной нулю? Отношение заряда протона к его массе равно 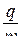=10⁸ Кл/кг.

 

Решение:

Протон – частица, несущая положительный заряд. Со стороны электрического поля на нее действует сила в направлении силовых линий. В данном случае эта сила направлена противоположно скорости частицы, поэтому скорость протона будет уменьшаться по мере его движения в поле до нуля, а затем начнется движение в противоположном начальному направлении. В этом усматривается аналогия с движением тела, брошенного вверх в поле тяготения Земли. Электростатическое поле, как и гравитационное, потенциально: заряженная частица обладает в этом поле потенциальной энергией.

При движении протона в электростатическом поле на него не действуют непотенциальные силы, поэтому выполняется закон сохранения полной механической энергии. Отсюда следует, что в положениях 1 и 2 суммы кинетической и потенциальной энергии протона равны между собой:

,

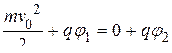 Þ .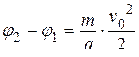

А искомая разность потенциалов равна

.

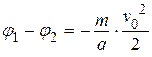Знак «–» означает. что протон движется в сторону большего потенциала.

Рассмотренное выше рассуждение широко применяется при использовании понятия ускоряющей разности потенциалов.

Заметим, что физический смысл имеет не само значение потенциала, а разность потенциалов между двумя точками, что и отражено в приведенных выше рассуждениях. А значение потенциала в некоторой точке определяется, в соответствии с этим, лишь относительно другой точки, выбранной в качестве нулевой (значение потенциала в которой условно принимается равным нулю).

Для ответа на второй вопрос задачи рассмотрим равнозамедленное движение протона под действием электрической силы 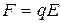. По второму закону Ньютона для протона ускорение равно

.

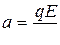Зависимость модуля скорости от времени при равнозамедленном движении имеет вид

,

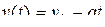тогда 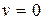 при 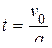. Подставляя выражение для ускорения, получаем искомое время:

.

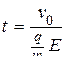Вычисления: 

 

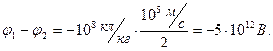
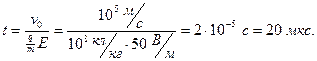
Ответ: , .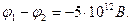

 

 

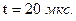Задача 3. Батарею из двух конденсаторов ёмкостью 400 и 500 пФ. Соединили последовательно и включили в сеть с напряжением 220 В. Потом батарею отключили от сети, конденсаторы разъединили и соединили параллельно обкладками, имеющими одноимённые заряды. Каким будет напряжение на зажимах полученной батареи.

 

Решение:

    У последовательно соединённых конденсаторов заряды на обкладках равны по модулю  и заряд батареи равен заряду одного конденсатора. Ёмкость батареи последовательно соединённых конденсаторов определяется по формуле 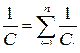. Для батареи из двух конденсаторов  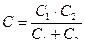 , а их заряд

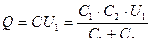.                                                                                    (1)

При отключении конденсаторов от сети их заряд сохраняется. У параллельно соединённых конденсаторов заряд батареи равен сумме зарядов конденсаторов 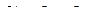, а ёмкость – сумме емкостей .

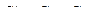Напряжение на зажимах батареи из двух параллельно соединённых конденсаторов

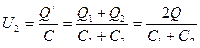                                                                               (2)

Подставляя (1) в (2), получаем

 

 

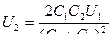
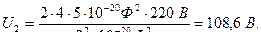
Ответ: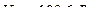

 

Задача 4. Сила тока в проводнике сопротивлением R=10 Ом за время Dt=50 с равномерно возрастает от I₁=5 А до I₂=10 А. Определите: 1) заряд, протекший через поперечное сечение проводника за указанное время; 2) количество теплоты, выделившееся за это время в проводнике.

 

Решение:

Из кинематики известно, что в случае равномерного возрастания скорости (равноускоренное движение) средняя на участке скорость равна среднему арифметическому от значений скорости в начале и в конце рассматриваемого участка движения. По аналогии найдем в данном случае среднее значение силы ток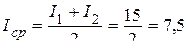а:

 (А).

Тогда также, как, зная среднюю скорость, находится весь пройденный путь, суммарный прошедший через поперечное сечение заряд будет равен

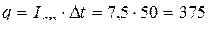 (Кл).

Будем теперь искать количество теплоты, выделившееся за это время в проводнике.

Прежде всего, найдем искомое значение в соответствии с законом Джоуля-Ленца:

,

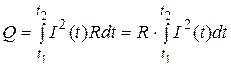Нетрудно видеть, что сила тока меняется по закону

.

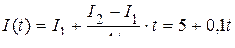Подставляем и вычисляем

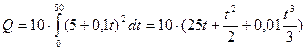=29,17 (кДж).

Ответ: Q=29,17кДж.

 

Задача 5.  По круговому витку радиуса r=0,1 м циркулирует ток силы          I=1 А. Найдите магнитную индукцию В: а) в центре витка; б) на оси витка на расстоянии b=0,1 м от его центра. 

 

Решение:  

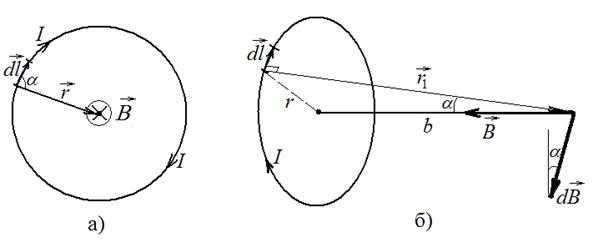
а) Магнитная индукция элементарного поля в центре витка по закону Био-Савара-Лапласа равна

,

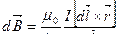т.е. вектор 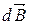 перпендикулярен плоскости рисунка (см. рис. а) и численно равен

.

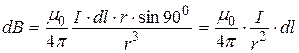Учитывая, что все элементы тока на круговом витке одинаково расположены по отношению к центру витка, получим

.

 

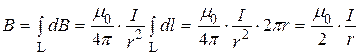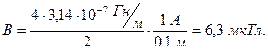
б) Магнитная индукция элементарного поля на оси витка по закону Био-Савара-Лапласа равна

.

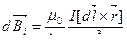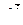Отсюда ясно (по определению векторного произведения), что вектор  перпендикулярен плоскости, образованной векторами  и , т.е. для каждого элемента тока вдоль витка  имеет свое направление. Совокупность векторов  образует коническую поверхность, ось которой совпадает с осью витка (рис.б)). Векторная сумма всех  с учетом симметрии будет направлена по оси витка и численно равна сумме проекций отдельных  на эту ось:

.

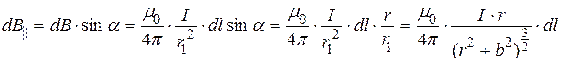Учитывая, что все элементы тока на круговом витке равноценно расположены по отношению к центру витка, получим

.

 

 

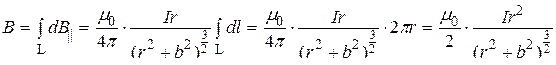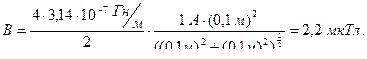
Ответ: а) В=6,3 мкТл, в) В=2,2 мкТл.

Задача 6. Согласно теории Бора, электрон в атоме водорода движется вокруг ядра по круговой орбите радиусом r=52,8 пм. Определите магнитную индукцию В поля, создаваемого электроном в центре круговой орбиты.  

 

Решение:

Будем находить величину магнитной индукции поля, созданного движущимся электрическим зарядом, исходя из формулы

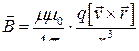
В скалярном виде для движущегося электрона в вакууме

,                                     

 

 

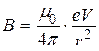где скорость движения электрона найдем из второго закона Ньютона, считая, что центростремительное ускорение электрону сообщает кулоновская сила его взаимодействия с положительно заряженным ядром:

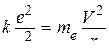 Þ ,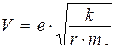

тогда искомая величина равна

.

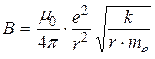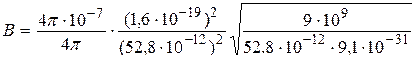=12,568 (Тл).

 

Ответ: В=12,568 Тл.

 

Задача 7. Тонкий медный проводник массой 1 г согнут в виде квадрата и концы его замкнуты. Квадрат помещен в однородное магнитное поле (В=0,1 Тл) так, что плоскость его перпендикулярна линиям индукции поля. Определите количество электричества q, которое протечет по проводнику, если квадрат, потянув за противоположные вершины, вытянуть в линию.

 

Решение:

При вытягивании квадрата в линию меняется магнитный поток сквозь ограниченную им площадь с начальной величины

,

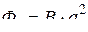где 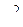 – площадь квадрата со стороной а, до нуля. При этом по закону электромагнитной индукции в замкнутом контуре возникает ЭДС индукции, среднее значение которой равно

.

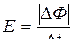где 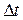 - время вытягивания квадрата в линию. Получаем:

.

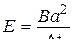Далее по закону Ома в контуре возникнет ток, среднее значение которого равно

,

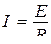где R – сопротивление проводника квадрата, которое найдем, зная материал и размеры линейного проводника:

,

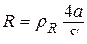где 4а – периметр квадрата, S – площадь поперечного сечения проводника, 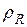 - удельное сопротивление меди.

Наконец, исходя из определения силы тока найдем суммарный заряд, прошедший по проводнику:

.

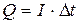Осталось связать линейные размеры квадрата и площадь поперечного сечения проводника с массой меди и ее плотностью :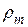

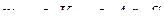 Þ .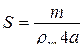

Получаем:

.

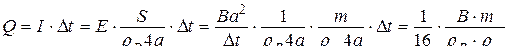Вычислим

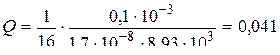 (Кл)

Ответ: Q=0,041 Кл.

 

 

Задача 8. Плоский квадратный контур со стороной 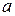=10 см, по которому течет ток 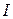=100 А, свободно установился в однородном магнитном поле ( 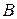=1 Тл). Определить работу 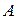, совершаемую внешними силами при повороте контура относительно оси, проходящей через середину его противоположных сторон, на угол: 1) =90⁰; 2) =3⁰. При повороте контура сила тока в нем поддерживается неизменной.

 

 

Решение:

 Как известно, на контур с током в магнитном поле действует момент сил:

                                        .                                                  

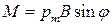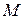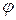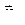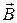По условию задачи, в начальном положении контур свободно установился в магнитном поле. При этом момент сил равен нулю ( =0), а значит =0, т.е. векторы  и  совпадают по направлению.

Если внешние силы выведут контур из положения равновесия, то возникший момент сил, будет стремиться возвратить контур в исходное положение. Против этого момента и будет совершаться работа внешними силами. Так как момент сил переменный (зависит от угла поворота 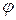), то для подсчета работы применим формулу работы в дифференциальной форме:

                                           .

Подставив сюда выражение 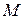 и учтя, что 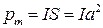, где 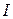 - сила тока в контуре;  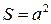- площадь контура, получим:

                                     .                                               

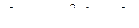Взяв интеграл от этого выражения, найдем работу при повороте на конечный угол:

                              .                                        

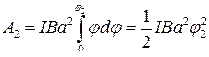Выразим угол  в радианах. После подстановки числовых значений величин  найдем:

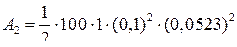   Дж = 1,37×10^-3 Дж = 1,37 мДж.

 

КОНТРОЛЬНАЯ РАБОТА №2

1. Тонкий стержень длиной 30 см несет равномерно распределенный по длине заряд с линейной плотностью 1 мкКл/м. На расстоянии 20 см от стержня находится точечный заряд 10^-2 мкКл. Заряд равноудален от концов стержня. Определить силу взаимодействия точечного заряда с заряженным стержнем.

2. Найти напряженность поля, созданного двумя параллельными бесконечными заряженными плоскостями с поверхностной плотностью:

а) σ₁ = +0,4 мКл/м², σ₂ = +0,1 мКл/м2; б) σ₁ = +0,4 мКл/м², σ₂ = - 0,1 мКл/м2.

3. Электрическое поле создано: а) сферической поверхностью радиуса R с поверхностной плотностью заряда σ; б) сферой радиуса R, заряженной с объемной плотностью ρ. Найти напряженность поля на расстоянии r от поверхности сферы в трех случаях: r > R,  r = R, r < R.

4. Положительные заряды 4 мкКл и 0,4 мкКл находятся в вакууме на расстоянии 1,5 м друг от друга. Определить работу, которую надо совершить, чтобы а) сблизить заряды до 1 м; б) удалить их на бесконечность.

5. Заряд q равномерно распределен по кольцу радиуса R. Найти потенциал относительно бесконечности на оси кольца как функцию расстояния h от центра кольца. Найти напряженность поля как функцию h.

6. Два одинаковых металлических шарика имеют положительные заряды 1,67×10 ^–9 и 6,67×10 ^–9 Кл и расположены на расстоянии 10 см друг от друга. Изменится ли сила взаимодействия после того, как их на короткое время соединить? Какой заряд будет на каждом шаре после соединения? Сколько электронов перешло при соприкосновении от одного шарика к другому?

7. Отрицательный точечный заряд –5q и положительный +2q закреплены на расстоянии r друг от друга. Где следует поместить положительный заряд Q, чтобы он находился в равновесии?

8.  Проводящий шарик, несущий заряд 1,8×10 ^–8 Кл, привели в соприкосновение с двумя такими же шариками, один из которых имел

заряд  -0,3×10 ^–8 Кл, а другой был не заряжен. Как распределился заряд между шариками? С какой силой будут взаимодействовать два из них в вакууме на расстоянии 5 см?

9.  Заряды 40 и –10 нКл расположены на расстоянии 10 см друг от друга. Какой надо взять третий заряд и где его надо поместить, чтобы система находилась в равновесии? Будет ли равновесие устойчивым или неустойчивым?

10. В однородном электрическом поле, вектор напряженности которого направлен вертикально вверх, находится в равновесии пылинка массой 0,03 г и зарядом 3 пКл. Определите напряженность поля.

11.  Вокруг точечного заряда 5 нКл по окружности радиусом 3 см

с угловой скоростью 5 рад/с вращается маленький отрицательно заряженный шарик. Найдите отношение заряда шарика к его массе (в мкКл/кг).

12.  Определите разность потенциалов электрического поля между точками 1 и 2, если известно, что электрон, двигаясь в этом электрическом поле в отсутствии других сил, в точке 1 имел скорость 10⁹ см/с, а в точке 2 – скорость 2×10⁹ см/с. Чему была бы равна скорость электрона в точке 2, если бы в точке 1 электрон имел нулевую скорость.

13. В электронной лампе электроны «ускоряются разностью потенциалов»

220 В. Чему равна скорость электронов при попадании их на анод?      

14. Электрон, летящий со скоростью 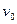, попадает в однородное поле заряженного конденсатора и вылетает из него под углом a. Найдите напряженность поля конденсатора, зная длину l конденсатора, массу и заряд электрона.

15. Какую скорость приобретает частица массой 0,1 г с зарядом 4 мкКл за

1 мин, двигаясь в однородном электростатическом поле с напряженностью 1000 В/м? Силу тяжести не учитывать.

16. Электростатическое поле создается положительно заряженной бесконечной нитью. Протон, двигаясь от нити под действием поля вдоль линии напряженности с расстояния r₁= 1 см до r₂= 5 см, изменил свою скорость от 1 до 10 Мм/с. Определите линейную плотность заряда нити.

17. На какое расстояние (в см) был перемещен заряд 70 мкКл вдоль линии напряженности однородного электрического поля, если при этом полем была совершена работа 1,4 мДж? Напряженность поля равна 200 В/м.

18. Два одинаковых отрицательных точечных заряда 100 нКл с массой 0,3 г движутся по окружности радиусом 10 см вокруг положительного заряда 100 нКл. При этом отрицательные заряды находятся на концах одного диаметра. Найдите угловую скорость вращения зарядов.

19.  Два заряда –q и 9q находятся на расстоянии d друг от друга. Со стороны отрицательного заряда по линии, проходящей через эти заряды, движется по направлению к ним заряд q. Какой минимальной кинетической энергией он должен обладать на бесконечности, чтобы попасть в точку, где находится отрицательный заряд?

20. При переносе точечного заряда q=10 нКл из бесконечности в точку, находящуюся на расстоянии r=20 см от поверхности равномерно заряженного шара, необходимо совершить работу A=0,5 мкДж. Радиус шара   R=4 см. Найдите потенциал j на поверхности шара и плотность распределения заряда. Потенциал на бесконечности принять равным нулю.

21. Плоский конденсатор, площадь каждой пластины которого 400 см², заполнен двумя слоями диэлектрика. Граница между ними параллельна обкладкам. Первый слой-прессшпан (ε₁ = 2) толщиной 0,2 см; второй слой-стекло (ε₂ = 7) толщиной 0,3 см. Конденсатор заряжен до разности потенциалов 600 В. Найти энергию конденсатора.

22. Чему равна емкость (в мкФ) конденсатора, если при увеличении его заряда на 30 мкКл разность потенциалов между пластинами увеличивается на 10 В?

23. Плоский воздушный конденсатор емкостью 1 мкФ соединили с источником тока, в результате чего он приобрел заряд 10 мкКл. Расстояние между пластинами конденсатора 5 мм. Определите напряженность поля  (в кВ/м) внутри конденсатора.

24. Расстояние между пластинами плоского конденсатора равно 2 см. Пластины заряжены до разности потенциалов 100 В. Чему будет равна разность потенциалов между пластинами, если, не изменяя заряда, расстояние между ними увеличить до 8 см?

25. Одну пластину незаряженного конденсатора, обладающего емкостью 1 нФ, заземляют, а другую присоединяют длинным тонким проводом к удаленному проводящему шару радиусом 20 см, имеющему заряд  92 мкКл. Какой заряд

(в мкКл) останется на шаре?

26.Конденсатору емкостью 2 мкФ сообщен заряд 0,01 Кл. Обкладки конденсатора соединили проводником. Найдите количество теплоты, выделившееся в проводнике при разрядке конденсатора.

27. Плоский воздушный конденсатор заполнили керосином, зарядили, сообщив ему энергию 2×10^-5Дж, и отключили от источника тока. Определите, какая энергия (в мкДж) будет запасена в конденсаторе, если из него слить керосин.

28. Стеклянная пластина целиком заполняет зазор между обкладками плоского конденсатора, емкость которого в отсутствии пластинки равна      2мкФ. Конденсатор зарядили от источника с ЭДС 1000В, после чего отключили от источника. Найдите механическую работу, которую необходимо совершить против электрических сил, чтобы извлечь пластину из конденсатора.

29. К пластинам плоского воздушного конденсатора приложена разность потенциалов 500 В. Площадь пластин 200см², расстояние между ними   1,5мм. Пластины раздвинули до расстояния 15мм. Найдите энергии конденсатора до и после раздвижения пластин, если источник тока перед раздвижением:

1) отключался; 2) не отключался.

30. Плоский воздушный конденсатор емкостью 10 пФ заряжен до разности потенциалов 500В. После отключения конденсатора от источника напряжения расстояние между пластинами конденсатора было увеличено в    3 раза. Определите: 1) разность потенциалов на пластинах конденсатора после их раздвижения; 2) работу сил по раздвижению пластин.

31. Аккумуляторная батарея, замкнутая на реостат сопротивлением

20 Ом, создает в нем ток 1,170 А. При увеличении сопротивления в 3 раза ток уменьшается до 0,397 А. Определите ЭДС и внутреннее сопротивление источника, а также силу тока короткого замыкания.

32.  В сеть с напряжением 100 В подключили резистор с сопротивлением       

2 кОм и вольтметр, соединенные последовательно. Вольтметр показывает 80 В. Когда резистор заменили другим, вольтметр показал 60 В. Определите сопротивление другого резистора.

33. Какую допускают относительную ошибку в измерении ЭДС источника, если показание вольтметра, присоединенного к его полюсам, принимают за ЭДС? Внутреннее сопротивлении е источника тока равно 0,9 Ом, сопротивление вольтметра 200 Ом.

34. Требуется определить падение напряжения на сопротивлении R. Для этого к концам сопротивления подключают вольтметр. Какая относительная погрешность будет допущена при измерениях, если показания вольтметра принять за то, которое имело место до его подключения? Сила тока в цепи поддерживается постоянной. Сопротивление вольтметра .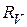

35. На рис. R₁= R,  R₂= 2R, R₃= 3R, R₄= 4R, . Определите заряд на конденсаторе.

 

 

 

36.  Для измерения тока в цепи с сопротивлением R включен амперметр. Какая относительная ошибка будет допущена, если считать, что включение амперметра не изменило тока? Напряжение на концах цепи поддерживается постоянным. Сопротивление амперметра .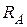

37.  Амперметр с внутренним сопротивлением 2 Ом, подключенный к зажимам источника, показывает ток 5 А. Если к зажимам этого источника подключить вольтметр с внутренним сопротивлением 150 Ом, то он покажет напряжение 12 В. Чему равен ток короткого замыкания?

38. ЭДС источника равна 24 В, сопротивление внешней цепи 10 Ом, падение потенциала внутри источника 4 В. Определите: 1) напряжение на зажимах источника; 2) внутреннее сопротивление источника; 3) мощность, потребляемую внешней цепью.

39.  Электрический чайник имеет 2 обмотки. При включении одной из них вода в чайнике закипает через 15 мин, при включении другой – через  30 мин. Через какое время закипит вода в чайнике, если включить 2 обмотки:

1) последовательно; 2) параллельно.

40. ЭДС источника составляет 12 В. Наибольшая сила тока, обеспечиваемая источником, равна 6 А. Определите максимальную мощность, которая может выделиться во внешней цепи такого источника и его максимальный КПД.

41. Определите магнитную индукцию в центре кругового проволочного витка радиусом R=10 см, по которому течет ток I =1 А.

42. Напряженность Н магнитного поля в центре кругового витка с магнитным моментом 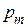=1,5 А×м² равна 150 А/м. Определите: 1) радиус витка; 2) силу тока в витке.

43. Согласно теории Бора, электрон в атоме водорода движется вокруг ядра по круговой орбите радиусом 52,8 пм. Определите магнитную индукцию В поля, создаваемого электроном в центре круговой орбиты.

44. Две небольшие одинаковые катушки расположены так, что их оси лежат на одной прямой. Расстояние между катушками l=2 м значительно превышает их линейные размеры. Число витков каждой катушки N=150, радиус витков r=50 мм. С какой силой F взаимодействуют катушки, когда по ним течет одинаковый ток I=1 А?

45. По двум бесконечно длинным прямым параллельным проводникам, расстояние между которыми 15 см, текут токи 70 А и 50 А в одном направлении. Определите магнитную индукцию 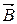 в точке, удаленной на 10 см от первого и

20 см от второго проводника.

46. По каждому из четырех длинных прямых параллельных провод­ников, проходящих через вершины квадрата (сторона квадрата 30 см) перпендикулярно его плоскости, течет ток 10 A, причем по трем провод­никам ток течет в одном направлении, а по четвертому — в противопо­ложном. Определите индукцию магнитного поля в центре квадрата.

47. Длинный прямой провод с током I=10А имеет участок в виде полуокружности радиуса R=12см. Определите индукцию магнитного поля в центре полуокружности.)

48.  Бесконечно длинный прямой проводник, по которому течет ток силой

I=5 A, согнут под прямым углом Найти индукцию магнитного поля на расстоянии a = 10 см от вершины угла в точках A и C, лежащих соответ­ственно на биссектрисе прямого угла и на продолжении од­ной из сторон (см. рис.)

,

 

 

49.  К тонкому однородному проволочному коль­цу радиуса r₀=10см подводят ток I=5А. Подводящие провода, располо­женные радиально, делят кольцо на две дуги, длины кото­рых  l₁/l₂ =2. Найти индукцию магнитного поля в центре кольца.

                          

 

           

 

50. Два параллельных бесконечно длинных провода, по которым текут в одном направлении токи I=60 А, расположены на расстоянии d =10 см друг от друга. Определить магнитную индукцию В в точке, отстоящей от одного про­водника на расстоянии г₁=5 см и от другого — на расстоянии r₂=12 см.    

 51. Электрон движется прямолинейно с постоянной скоростью 0,2 Мм/с. Определите магнитную индукцию В поля, создаваемого электроном в точке, находящейся на расстоянии 2 нм от электрона и лежащей на прямой, проходящей через мгновенное положение электрона и составляющей угол 45⁰ со скоростью движения электрона.

52.  Электрон движется прямолинейно и равномерно со скоростью

V=3,00×10⁵ м/с. Найти индукцию В поля, создаваемого электроном в точке, находящейся на расстоянии от него r =1,00×10^{-9 м (10 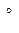) и лежащей на перпендикуляре к 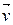, проходящем через мгновенное положение электрона.}   

53. Определите напряженность магнитного поля, создаваемого электроном, прямолинейно и равномерно движущимся со скоростью

5000 км/с, в точке, находящейся от него на расстоянии 10 нм и лежащей на перпендикуляре к скорости, проходящем через мгновенное положение электрона. 

54.  Два протона движутся параллельно друг другу с одинаковой скоростью 600 км/с. найти отношение сил электрического и магнитного взаимодействия этих частиц.

55.  Два равных точечных заряда 0,1 мкКл движутся навстречу друг другу со скоростью 100 км/с. Найти индукцию магнитного поля в точке на расстоянии 4 см от первого заряда и на расстоянии 3 см от второго в тот момент, когда расстояние между зарядами равно 5 см.

56. Два одинаковых точечных заряда 0,2 мкКл движутся в одной плоскости вдоль взаимно перпендикулярных прямых. Скорости зарядов разны 2 Мм/с и

3 Мм/с. В некоторый момент времени заряды оказываются на одинаковом расстоянии 10 см от точки пересечения их траекторий движения, удаляясь от этой точки. Определить в этот момент времени индукцию магнитного поля в точке пересечения траекторий зарядов. 

57. Два протона движутся параллельно друг другу с одинаковой
скоростью V=2 Мм/с на расстоянии а=20 см друг от друга. Определить максимальную индукцию магнитного поля на прямой, проходящей через середи­ну отрезка, соединяющего протоны, перпендикулярно к плоскости, в которой находятся траектории движения протонов.

58. Электрон, пройдя ускоряющую разность потенциа­лов U=400 В, попал в однородное магнитное поле с индукцией B=1,5 мТл. Определить:

1) радиус R кривизны траектории; 2) ча­стоту п вращения электрона в магнитном поле. Вектор скорости электрона перпендикулярен линиям индукции.

59. Электрон, имея скорость V=2 Мм/с, влетел в однородное магнитное поле с индукцией В=30 мТл под углом α=30° к направлению линий индукции. Определить радиус R и шаг h винтовой линии, по которой будет двигаться электрон.

60. Альфа-частица прошла ускоряющую разность потенциалов U=104 В и влетела в скрещенные под прямым углом электрическое (E=10 кВ/м) и магнитное (B=0,1 Тл) поля. Найти отношение заряда альфа-частицы к ее массе, если, двигаясь перпендикулярно обоим полям, частица не испытывает отклонений от прямолинейной траектории.

61. В однородном магнитном поле напряженностью Н=100 кА/м помещена квадратная рамка со стороной а=10 см. Плоскость рамки составляет с направлением магнитного поля угол a=60⁰. Определите магнитный поток, пронизывающий рамку.

62. Определите магнитный поток через площадь поперечного сечения катушки (без сердечника), имею­щей на каждом сантиметре длины n = 8 витков. Радиус соленоида r=2 см, а сила тока в нем I=2 А.

63. Какова скорость движения автомобиля, если в его вертикальной антене, длиной 1,5 м индуцируется ЭДС 6×10^-4 В. Горизонтальная составляющая магнитного поля Земли Н=14 А/м. Направление скорости перпендикулярно магнитному меридиану.

64. Железнодорожные рельсы изолированы друг от друга и от земли и соединены че­рез милливольтметр. Каково показание прибора, если по рельсам проходит поезд со ско­ростью 20 м/с? Вертикальную составляющую напряженности магнитного поля Земли принять равной 40 А/м, а расстояние между рельсами 1,54 м.

65. Тонкий медный провод массой m=5 г согнут в виде квадрата и концы его замкнуты. Квадрат помещен в однородное магнитное поле с индукцией В=0,2 Тл так, что его плоскость перпендикулярна линиям поля. определите заряд Q, который протечет по проводнику, если квадрат, потянув за противоположные вершины, вытянуть в линию. Плотность меди 8900 кг/м³, удельное сопротивление меди 1,7×10^-8 Ом×м.

66. Соленоид диаметром d=4 см, имеющий N=500 витков, помещен в магнитное поле, индукция которого изменяется со скоростью 1 мТл/с. Ось соленоида составляет с вектором магнитной индукции угол a=45⁰. Определить ЭДС индукции e, возникающей в соленоиде.

67.  При скорости изменения силы тока dI/dt в соле­ноиде, равной 50 А/с, на его концах возникает ЭДС самоиндук­ции ε=0,08 В. Определить индуктивность L соленоида.

68. В однородном магнитном поле с индукцией B=0,1 Тл равномерно вращается рамка, содержащая N = 1000 витков, с часто­той n=10 c ^-1. Площадь S рамки равна 150 см². Определить мгновен­ное значение ЭДС, соответствующее углу поворота рамки 30°.

69. Виток, по которому течет ток I=20 А, свободно уста­новится в однородном магнитном поле В=16 мТл. Диаметр d витка равен 10 см. Какую работу нужно совершать, чтобы медленно по­вернуть виток на угол α=π/2 относительно оси, совпадающей с диа­метром?

70. Обмотка соленоида состоит из одного слоя плотно прилегающих друг к другу витков медного провода диаметром d =0,2 мм. Диаметр D соленоида равен 5 см. По соленоиду течет ток I=1 А. Определить количество электричества Q, протекающее через обмотку, если концы ее замкнуть накоротко. Толщиной изо­ляции пренебречь.

71. Катушка диаметром 10 см, имеющая 500 витков, находится в магнитном поле. Чему будет равно среднее значение ЭДС индукции в этой катушке, если индукция магнитного поля увеличивается в течение 0,1 с от 0 до 2 Тл?

72.  В однородном магнитном поле, индукция которого 0,8 Тл, равномерно

вращается рамка с угловой скоростью 15 рад/с. Площадь рамки 150 см². Ось вращения находится в плоскости рамки и составляет 30⁰ с направлением силовых линий магнитного поля. Найти максимальную ЭДС индукции во вращающейся рамке.

73. В магнитном поле, индукция которого равна 0,05 Тл, помещена катушка, состоящая из 200 витков проволоки. Сопротивление катушки 40 Ом, площадь ее поперечного сечения 12 см². Катушка помещена так, что ее ось составляет 60⁰ с направлением поля. Какое количество электричества пройдет по катушке при исчезновении магнитного поля?

74.  Две катушки намотаны на один общий сердечник. Индуктивность

 первой катушки 0,2 Гн, второй - 0,8 Гн, сопротивление второй катушки 600 Ом. Какой ток потечет по второй катушке, если ток в 0,3А, текущий в первой катушке, выключить в течение 1 мс?

75. В однородном магнитном поле с индукцией 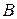=0,02 Тл равномерно

вращается вокруг вертикальной оси горизонтальный стержень длиной 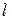=0,5 м. Ось вращения проходит через конец стержня параллельно линиям магнитной индукции. Определите число оборотов в секунду, при котором на концах стержня возникает разность потенциалов 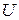=0,1 В.

76. Обмотка соленоида содержит 10 витков на каждый сантиметр длины.

При какой силе тока объемная плотность энергии магнитного поля будет равной 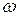=1 Дж/м³?

77. Соленоид, площадь сечения которого равна 5 см², содержит 1200 витков. Индукция магнитного поля внутри соленоида при токе силой 2 А равна 0,01 Тл. Определить индуктивность соленоида.

78. Сколько витков проволоки диаметром 0,4 мм с изоляцией ничтожной

толщины нужно намотать на картонный цилиндр диаметром 2 см, чтобы получить однослойную катушку с индуктивностью 1 мкГн? Витки вплотную прилегают друг к другу.

79. Сколько витков имеет катушка, индуктивность которой 1 мГн, если

при силе тока 1 А магнитный поток сквозь катушку равен 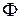=2 мкВб?

80. На картонный каркас длиной 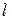=50 см и площадью сечения 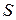=4 см²

намотан в один слой провод диаметром 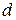=0,2 мм так, что витки плотно прилегают друг к другу (толщиной изоляции пренебречь). Определить индуктивность  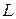получившегося соленоида.

КОЛЕБАНИЯ. ВОЛНЫ. ОПТИКА

Основные формулы