ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ, МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ
ОСНОВНЫЕ ФОРМУЛЫ
Кинематика
● Средняя и мгновенная скорости материальной точки
, 
,
, 
,
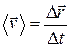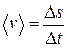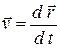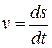где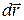 
- элементарное перемещение точки за промежуток времени 
; 
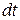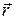- радиус-вектор точки; 
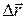- приращение радиус-вектора за время 
; 
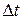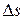- путь, пройденный материальной точкой за промежуток времени .
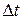● Среднее и мгновенное ускорения материальной точки
, 
.
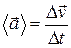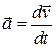●Полное ускорение при криволинейном движении
, 
,
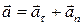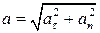где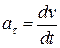 
- тангенциальная составляющая ускорения; 
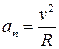- нормальная составляющая ускорения (R – радиус кривизны траектории в данной точке).
● При равнопеременном движении вдоль оси х координата и скорость тела определяются выражениями
, 
,
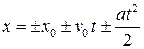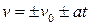где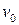 
– начальная скорость.
● Угловая скорость
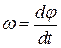или 
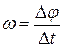(если ω=const)
● Угловое ускорение
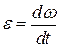или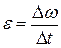 
(если ε=const).
● Период и частота вращения
; 
,
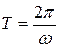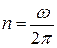где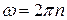 
- циклическая частота вращения, равная угловой скорости (если ω=const).
● Зависимость угла поворота и угловой скорости для равнопеременного вращательного движения от скорости
; 
,
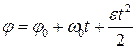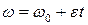где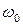 
- начальная угловая скорость, 
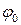- угол, определяющий начальное положение материальной точки.
● Связь между линейными и угловыми величинами:
,
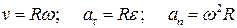где R – расстояние до оси вращения (радиус кривизны траектории).
Динамика материальной точки и поступательное движение
Твёрдого тела
● Импульс материальной точки
.
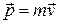● Второй закон Ньютона (основное уравнение динамики материальной очки)
.
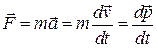● Сила трения скольжения
,
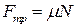где μ- коэффициент трения скольжения; N- сила нормального давления.
● Закон сохранения импульса для замкнутой системы
,
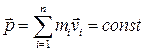где n- число материальных точек (или тел), входящих в систему.
Работа и энергия
● Элементарная работа, совершаемая постоянной силой F на элементарном перемещении ds,
,
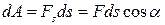где Fs- проекция силы на направление перемещения; α- угол между направлениями силы и перемещения.
● Работа, совершаемая силой, на пути S
.
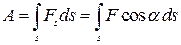● Работа постоянной силы
,
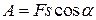где угол α – угол между направлением действия силы и направлением перемещения.
● Мгновенная мощность
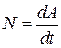, или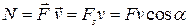 
.
● Кинетическая энергия движущегося тела
.
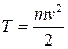● Связь между силой, действующей на тело в данной точке градиентного или потенциального (или консервативных сил) поля, и потенциальной энергией частицы
,
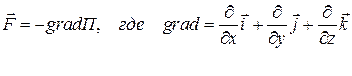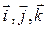- единичные векторы координатных осей.
● Потенциальная энергия тела, поднятого над поверхностью Земли на
высоту h (при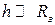 
),
,
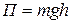где g- ускорение свободного падения.
● Сила упругости
,
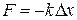где ∆х- абсолютное изменение длины; k- коэффициент упругости.
●Потенциальная энергия упругодеформированного тела
.
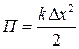● Закон сохранения механической энергии (для консервативной системы)
.
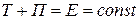Механика твёрдого тела
● Момент инерции материальной точки
,
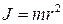где m- масса материальной точки; r- расстояние до оси вращения.
●Момент инерции системы материальных точек (тела)
,
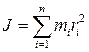где ri – расстояние от материальной точки массы mi до оси вращения. В случае непрерывного распределения массы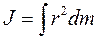 
.
●Теорема Штейнера
,
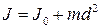где J0 – момент инерции относительно оси, проходящей через центр масс; J – момент инерции относительно произвольной оси, параллельной данной, отстоящей от первой на расстоянии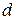 
; m- масса тела.
● Кинетическая энергия тела, вращающегося вокруг неподвижной оси z
,
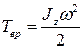где Jz- момент инерции тела относительно оси z; ω- его угловая скорость.
●Кинетическая энергия тела, движущегося поступательно без скольжения при одновременном вращении
,
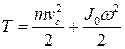где J0 – момент инерции относительно оси, проходящей через центр масс; m- масса тела;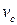 
– скорость центра масс тела; ω- угловая скорость тела.
● Момент силы относительно неподвижной точки
,
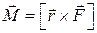где r – радиус-вектор, проведенный из этой точки в точку приложения силы F. Модуль момента силы
,
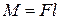где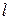 
- плечо силы (кратчайшее расстояние между линией действия силы и осью вращения).
● Работа при вращении тела
,
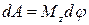где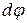 
- угол поворота тела; 
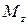- момент силы относительно оси z.
● Момент импульса
.
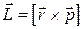● Момент импульса твердого тела относительно произвольной оси z
,
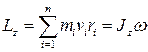где ri – расстояние от оси до отдельной частицы тела;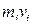 
- импульс этой частицы; Jz – момент инерции тела относительно оси z; ω – его угловая скорость.
● Уравнение (закон) динамики вращательного движения твердого тела
.
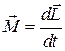● Уравнение (закон) динамики вращательного движения твердого тела относительно неподвижной оси z
,
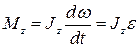где ε – угловое ускорение; Jz – момент инерции тела относительно оси z.
● Механическое напряжение при упругой деформации
,
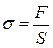где F- растягивающая (сжимающая) сила; S – площадь поперечного сечения.
● Закон Гука для продольного растяжения (сжатия)
,
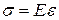где E – модуль Юнга, ε – относительное приращение длины стержня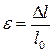 
.
Тяготение.
Элементы теории поля.
● Закон всемирного тяготения
,
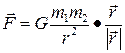где F – сила всемирного тяготения (гравитационная сила) двух материальных точек массами m1 и m2, находящихся на расстоянии r друг от друга; G – гравитационная постоянная (G=6.67∙10-11 н∙м2/кг2).
● Сила тяжести
,
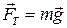где g – ускорение свободного падения.
● Напряженность поля тяготения
,
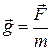где F – сила тяготения, действующая на материальную точку массой m, помещенную в данную точку поля.
● Потенциальная энергия гравитационного взаимодействия двух материальных точек массами m1 и m2, находящихся на расстоянии r друг от друга,
.
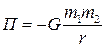Потенциал поля тяготения
,
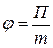где П – потенциальная энергия материальной точки массой m, помещенной в данную точку поля.
● Связь между потенциалом поля тяготения и его напряженностью
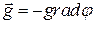
Элементы механики жидкостей
● Гидростатическое давление столба жидкости на глубине h
,
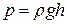где ρ – плотность жидкости.
● Закон Архимеда
,
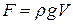где F – выталкивающая сила; V – объем погруженной части тела.
● Уравнение неразрывности
,
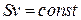где S – площадь поперечного сечения трубки тока; V – скорость жидкости.
● Уравнение Бернулли для стационарного течения идеальной несжимаемой жидкости
,
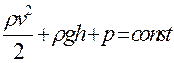где Р – статическое давление жидкости для определенного сечения трубки тока;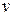 
– скорость жидкости для этого же сечения; 
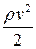- динамическое давление жидкости для этого же сечения; 
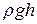- гидростатическое давление.
● Формула Торричелли, позволяющая определить скорость истечения жидкости из малого отверстия в открытом широком сосуде,
,
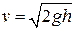где h – глубина, на которой находится отверстие относительно уровня жидкости в сосуде.
● сила внутреннего трения между слоями текущей жидкости
,
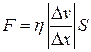где η – динамическая вязкость жидкости;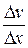 
- градиент скорости; S – площадь соприкасающихся слоев.
● Формула Стокса, позволяющая определить силу сопротивления, действующую на медленно движущийся в вязкой среде шарик,
,
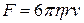где r – радиус шарика; 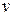- его скорость.
Дата: 2018-12-28, просмотров: 338.
