Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

● Уравнение состояния реальных газов (уравнение Ван-дер-Ваальса) для произвольной массы газа

,

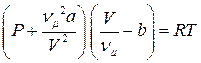где a и b – постоянные Ван-дер-Ваальса, различные для различных газов.

● Внутреннее давление, обусловленное силами взаимодействия молекул

,

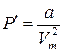где V_m – молярный объем.

● Внутренняя энергия реального газа

.

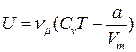● Поверхностное натяжение

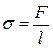, или ,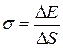

где F – сила поверхностного натяжения, действующая на контур 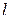, ограничивающий поверхность жидкости;  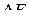- поверхностная энергия, связанная с площадью  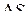поверхности пленки.

● Высота подъема жидкости в капиллярной трубке

,

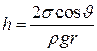где θ – краевой угол; r – радиус капилляра; ρ – плотность жидкости; g – ускорение свободного падения.

● Закон Дюлонга и Пти

,

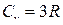где С_v – молярная (атомная) теплоемкость химически простых твердых тел.

 

Примеры решения задач

Задача 1. Движение материальной точки задано уравнением 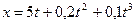(м). Определить скорость точки в моменты времени t₁=2 с и

t₂=4 с, а также среднюю скорость в интервале времени от t₁ до t₂.

 

Решение:

Точка прямолинейно движется вдоль оси OX. Модуль мгновенной скорости в этом случае

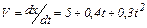 (м/с).

Найдем V ₁ и V ₂:

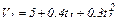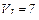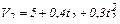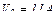 ,         м/с;

 ,         м/с.

Средняя скорость

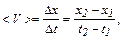
где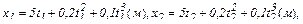

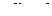 м/с.

 

Ответ: V ₁ =7 м/с, V ₂ =11,4 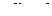м/с,  м/с

 

Задача 2. Тело массой 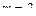 кг движется по вертикальной стене. Сила  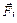действует под углом a = 30⁰ к вертикали. Коэффициент трения 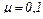. Найти величину силы 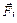, если ускорение тела направлено вверх и равно a = 2 м/с² .

 

Решение:

На тело действуют четыре силы: сила 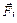, сила тяжести 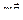, сила реакции опоры  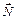и сила трения 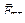. Покажем эти силы на рисунке.

Запишем II закон Ньютона в виде

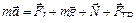.                                                                        (1)                                                                               Ось OY направим вертикально вверх, ось OX – перпендикулярно стене. В проекциях на оси координат уравнение (1) примет вид

OХ: 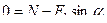                                                                                            (2)

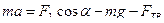OY: .                                                                           (3)                                                                    

Сила трения скольжения

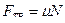.                                                                                                         (4)        

Используя (2) и (4), перепишем (3):

.

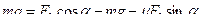Отсюда

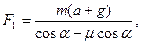
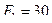 Н.

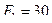Ответ:  Н.

Задача 3. Частица массой m₁, имеющая скорость V₂, налетела на покоящийся шар массой m₂  и отскочила от него со скоростью U ₁ под прямым углом к направлению первоначального движения. Какова скорость U₂ шара после соударения? Считать удар центральным.

 

Решение:

Используя закон сохранения импульса, получим

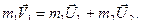
На рисунке покажем импульсы тел.

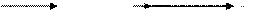Модуль импульса шара найдём, используя теорему Пифагора:

,

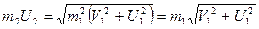отсюда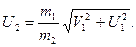

Ответ: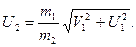

 

Задача 4. Шар массой M висит на нити длиной l. В шар попадает горизонтально летящая пуля и застревает в нём. С какой скоростью V ₀ должна лететь пуля, чтобы в результате попадания пули шар мог сделать на нити полный оборот в вертикальной плоскости? Размерами шара пренебречь. В верхней точке сила натяжения нити равна нулю. Масса пули m.

 

Решение:

 

 

 

Обозначим: V – скорость шара с пулей сразу после неупругого соударения, U – скорость шара с пулей в верхней точке.

В проекциях на ось OX закон сохранения импульса имеет вид

mV ₀ = ( m + M ) V.                                                                                                    (1)                                                                                      

Выберем нулевой уровень отсчёта потенциальной энергии, совпадающий с осью OX .

В нижнем положении шар с пулей обладает только кинетической энергией 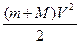; в верхней точке - кинетической  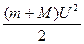и потенциальной ( m + M ) gh энергиями, где h = 2R =2 l.

Закон сохранения механической энергии запишем в виде

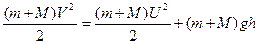 .                                                                    (2)              

После преобразований

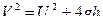.                                                                                    (2¢)

В верхней точке на шар с пулей действует сила тяжести, по условию задачи сила натяжения нити равна нулю. Используем II закон Ньютона:

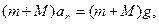                                                                        (3)

где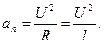

Из уравнения (1) выразим V ₀:

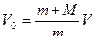_.                                                                                                                                         (4)

Из уравнения (3)

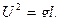                                                                                                 (5)

Подставив (5) в (2¢), получим

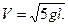
Найдем V ₀ , вернувшись к (4)

 

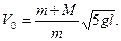
Ответ: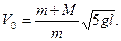

 

Задача 5. По наклонной плоскости, образующей угол a с горизонтом, скатывается без скольжения 1) сплошной однородный диск, 2) шар. Определить линейное ускорение их центров. Предварительно вывести общую формулу.

 

Решение:

Тело участвует в сложном движении:

1)поступательно движется вниз по наклонной плоскости;

2) вращается вокруг оси, проходящей через центр тяжести.

На рисунке покажем силы, действующие на тело.

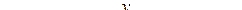Для поступательного движения запишем II закон Ньютона в проекциях на ось OX.

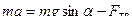.                                                                             (1)

Для вращательного движения используем закон

,                                                                                                 (2)

где 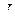- момент инерции,  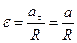- угловое ускорение.

Момент силы 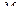 создает сила трения, плечо которой равно R, две другие силы не создают вращающего момента.

.

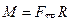Перепишем (2):

.

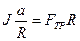Выразим силу трения из (3) и подставим в (1):

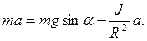
Отсюда

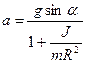 .                                                                                        (4)

Зная моменты инерции диска и шара

,

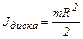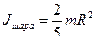
найдем ускорения диска и шара

,

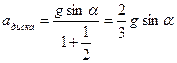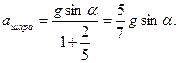
Ответ: ,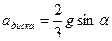

 

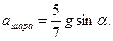
Задача 6. Две частицы движутся навстречу друг другу со скоростями 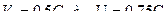. Найти их относительную скорость.

 

Решение:

Согласно теореме сложения скоростей в теории относительности,

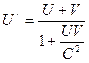, где 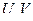-скорости первой и второй частицы; 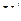- их относительная скорость: С- скорость света в вакууме.

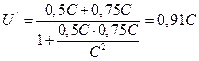
Это означает, что, во первых, ни в какой инерциальной системе отсчёта скорость процесса не может превзойти скорость света, и, во вторых, скорость распространения света в вакууме абсолютна.

Ответ: = 0,91С.

 

Задача 7. В баллоне объёмом 20 л находится аргон под давлением 1,0 Мпа и температуре 300 К. После того как из баллона было взято 20,0 г аргона, температура в баллоне понизилась до 280 К. Определить давление газа, оставшегося в баллоне.

 

                                    Решение:

Для решения задачи воспользуемся    уравнением состояния идеального    газа, применив его к начальному и конечному состояниям газа:

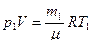,                                                             (1)

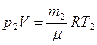                         .                                                              (2)            

Из уравнений (1) и (2) выразим m₁ и m₂ и найдём их разность:

,

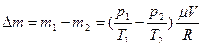откуда находим

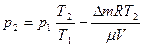 .                                                       (3)          

Проверку решения проведем по размерности физических величин. В правую часть вместо символов величин подставим их единицы измерения. В правой части два слагаемых. Первое из них имеет размерность давления, так как состоит из двух множителей, первый из которых – давление, а второй – безразмерный. Проверим второе слагаемое:

.

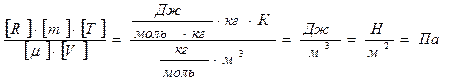
Вычисления произведём по формуле (3) с учётом, что для аргона 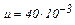 кг/моль.

 

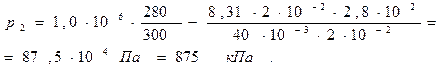
Ответ: 875 кПа

Задача 8 . Во сколько раз следует изотермически увеличить объем идеального газа в количестве 3 моль, чтобы его энтропия увеличилась на

 25 Дж/К?

                         Решение:

Для обратимого процесса ,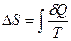

       где .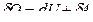

Так как процесс изотермический, то для идеального газа 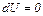, а элементарная работа равна

.

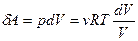Изменение энтропии 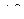 для изотермического процесса будет равно

.

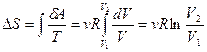Из последнего соотношения находим

.

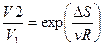Показатель экспоненты – величина безразмерная.

Вычисления: .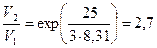

Ответ: .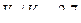

 

КОНТРОЛЬНАЯ РАБОТА №1

1. Движение точки по окружности радиусом R = 200 см задано уравнением S = 2t³ (м). В какой момент времени нормальная составляющая ускорения a_n точки будет равна ее тангенциальной составляющей a_τ? Определить полное ускорение а в этот момент.

2. Движение точки в плоскости XY задано уравнениями X = 2t–0,5t³ (м),

Y = 2t – t² (м). Определить скорость точки V к концу второй секунды.

3. По дуге окружности радиусом R = 10 м движется точка. В некоторый момент времени нормальная составляющая ускорения a_n = 4,0 м/с², а векторы полного и нормального ускорений образуют угол α = 60⁰. Найти скорость и тангенциальную составляющую ускорения точки.

4. Движение точки по окружности радиусом R = 4 м задано уравнением

 S = 10 + t² – 2t. Найти тангенциальное a_τ , нормальное a_n и полное а ускорения точки в момент времени t = 2 с.

5. Движение материальной точки задано уравнением Х = 4t -0,05t². Определить момент времени, в который скорость точки равна нулю. Найти координату и ускорение точки в этот момент. Построить графики зависимости координаты, пути, скорости и ускорения этого движения от времени.

6. Путь, пройденный телом, задан уравнением S = 2t – t² + t³ (м). Найти среднюю скорость тела в интервале от 1 до 5 с.

7. Путь, пройденный телом, задан уравнением S = 2 + 12t -6t² + 4t³ (см). Найти среднее ускорение тела в интервале от 1 до 4 с.

8. Путь, пройденный точкой по окружности радиусом R = 7 см, задан уравнением S = 4 + 2t + 0,5t² (см). Определить полное ускорение a точки к концу пятой секунды.

9. Частота маховика уменьшалась с n₀ = 10 об/с до n = 6 об/с. За время торможения он сделал N = 50 оборотов. Определить угловое ускорение маховика e и продолжительность торможения t.

10. Тело вращается вокруг неподвижной оси. Угол поворота задан уравнением φ = 6t -2t³. Найти угловое ускорение тела e в момент его остановки.

11. Наклонная плоскость, образующая с горизонтом угол α = 30⁰, имеет длину L = 167 см. За какое время тело соскользнет с нее, если коэффициент трения тела о плоскость μ = 0,2?

12. Автомобиль массой m = 2,5 т поднимается в гору (α = 30⁰) ускоренно и за время t = 5 мин проходит путь S = 9 км. Начальная скорость автомобиля V₀ = 1 м/с, а коэффициент трения μ = 0,1. Какова сила тяги мотора автомобиля F?

13. Брусок соскальзывает с наклонной плоскости, образующей с горизонтом угол α = 30⁰. Каково ускорение бруска, если коэффициент трения его о поверхность плоскости μ = 0,4?

14. За какое время тяжелое тело спустится с вершины наклонной плоскости, высота которой h = 2 м, угол наклона α = 45⁰? Предельный угол, при котором тело находится в покое, для этой плоскости равен α_пр = 30⁰.

15. Наклонная плоскость образует с горизонтом угол α = 30⁰. Ее длина

L = 2 м. Тело, двигаясь равноускоренно, соскользнуло с этой плоскости за время t = 2 с. Определить коэффициент трения тела о плоскость μ.

16. Тело скользит вниз по наклонной плоскости, составляющей с горизонтом угол α = 30⁰. Ее длина L = 2 м, коэффициент трения тела о плоскость μ = 0,2. Какова скорость тела в конце наклонной плоскости, если его начальная скорость

V₀ = 0?

17. Тело скользит вниз по наклонной плоскости, составляющей с горизонтом угол α = 30⁰. Зависимость пройденного телом расстояния S от времени t дается уравнением S = ct², где с = 1,5 м/с². Найти коэффициент трения тела о плоскость μ.

18. На наклонной плоскости длиной L = 13 м и высотой h = 5 м лежит груз массой m = 26 кг. Коэффициент трения груза о плоскость μ = 0,5. Какую силу F надо приложить к грузу: а) чтобы втащить груз; б) чтобы стащить груз?

19. Мальчик тянет по горизонтальной дороге санки с грузом. С каким ускорением a движутся санки, если сила тяги F = 200 Н, а веревка образует с горизонтом угол α = 45⁰? Масса санок m = 50 кг. Коэффициент трения полозьев санок μ = 0,1.

 

 

 

20. Два связанных груза массами m₁ = 3 кг и m₂ = 5 кг лежат на горизонтальном столе, шнур разрывается при натяжении Т = 24 Н. Какую максимальную силу F можно приложить к грузу массой m₁? Коэффициент трения принять равным μ = 0,2.

21 .Тело массой m = 2,0 кг падает с высоты h = 20 м из состояния покоя и в момент удара о землю имеет скорость V = 15 м/с. Определить работу силы сопротивления и силу сопротивления, считая её постоянной.

22. Какой путь s пройдут санки по горизонтальной поверхности после спуска с горы высотой h = 1,5 м и уклоном α = 45⁰? Коэффициент трения μ = 0,2.

23. Ящик тянут равномерно за верёвку. Сила F направлена под углом α = 30⁰. Определить работу, которую при этом совершают. Масса ящика m = 100 кг, коэффициент трения μ = 0,33, путь S = 50 м.

24. Поезд из состояния покоя за время τ = 5 мин развивает скорость

V = 64,8 км/ч. Масса поезда m = 600 т, коэффициент трения μ = 0,04. Найти среднюю мощность, развиваемую локомотивом, если его движение равноускоренное.

25. Какую среднюю мощность развивает автомобиль при подъеме в гору? Начальная скорость автомобиля V₀= 36 км/ч, его конечная скорость

V_к= 21 ,6 км/ч, коэффициент трения μ = 0,1, высота горы h = 12 м, длина склона горы L= 80 м, масса автомобиля m = 4×1О³ кг.

26. Какую нужно совершить работу A, чтобы пружину жесткостью

k = 800 Н/м, сжатую на Dx₁ = 6 см, дополнительно сжать на ∆х₂ = 8 см?

27. Санки скатываются с горки высотой h = 8 м по склону длиной L = 100 м. Масса санок с седоком m = 60 кг. Какова сила сопротивления движению санок, если в конце спуска они имели скорость V = 11 м/с?

28. Вагонетку массой m = 100 кг поднимают по рельсам в гору с ускорением

 a = 0,2 м/с². Коэффициент трения колес вагонетки о рельсы μ = 0,1, длина склона горы L = 50 м, угол наклона α = 30⁰. Какова работа A силы тяги?

29. Самолет для взлета должен иметь скорость V = 80 км/ч. Длина разбега

S = 150 м. Какова мощность моторов при взлете, если масса самолета m = 1000 кг, коэффициент трения колес шасси о землю μ = 0,02?

30. На горизонтальном участке пути длиной S = 2 км скорость поезда возросла с V₁ = 36 до V₂ = 72 км/ч. Определить работу и среднюю мощность тепловоза, если масса поезда m = 10³ т, а коэффициент трения m = 0,001.

31. В подвешенный на нити длиной L = 1,8 м деревянный шар массой

m₁ = 8 кг попадает горизонтально летящая пуля массой m₂ = 4 г. С какой скоростью летела пуля, если нить с шаром и застрявшей в нем пулей отклонилась от вертикали на угол α = 3⁰?

32. Грузы массами m₁ = 10 кг и m₂ = 15 кг подвешены на нитях длиной

L = 2 м так, что они соприкасается между собой. Меньший груз был отклонен на угол α = 60⁰ и отпущен. На какую высоту поднимутся грузы после неупругого удара?

33. Шар массой m₁ = 3 кг движется со скоростью V₁ = 2 м/с и сталкивается с покоящимся шаром массой m₂ = 5 кг. Удар абсолютно неупругий. Какая работа совершается при деформации шаров?

34. Шары массами m₁ = 2 кг и m₂ = 3 кг двигаются навстречу друг другу со скоростями V₁ = 8 м/с, V₂  = 4 м/с. Найти работу деформации шаров при их абсолютно неупругом столкновении.

35. Пуля попадает в ящик с песком и застревает в нем. На сколько сожмется пружина жесткостью k, удерживающая ящик, если пуля имеет массу m и движется со скоростью V, а масса ящика с песком М?  Поверхность гладкая.

36. От удара груза массой M = 50 кг, падающего свободно с высоты

h = 4 м, свая массой m = 150 кг погружается в грунт на глубину

DS=10 см. Определить силу сопротивления грунта, считая ее постоянной, а удар абсолютно неупругим.

37. Вагон массой 20 т, движущийся по горизонтальному пути со скоростью

2 м/с, догоняет вагон массой 40 т, движущийся со скоростью  1 м/с, и сцепляется с ним. Найти изменение механической энергии системы двух вагонов.

38. Два шара подвешены на тонких параллельных нитях и касаются друг друга. Меньший шар отводят на 90⁰ от первоначального положения и отпускают. После удара шары поднялись на одинаковую высоту. Определить массу меньшего шара, если масса большего 0,6 кг, а удар абсолютно упругий.

39. Два упругих шарика, массы которых m₁ = 100 г и m₂ = 300 г, подвешены на одинаковых нитях длиной l = 50 см и касаются друг друга. Первый шарик отклонили от положения равновесия на угол a = 90⁰ и отпустили. На какую высоту поднимется второй шарик после абсолютно упругого удара?

40. Два шара подвешены на параллельных нитях одинаковой длины так, что они соприкасаются. Масса первого шара m₁ = 0,2 кг, масса второго

m₂ = 100 г. Первый шар отклоняют так, что его центр поднимается на высоту

 h = 4,5 см, и отпускают. На какую высоту поднимутся шары после соударения, если удар абсолютно неупругий?

41. Через блок в виде однородного сплошного диска, имеющего массу

 m = 500 г, перекинута тонкая гибкая нить, к концам которой подвешены грузы массами m₁ = 100 г и m₂ = 120 г. С каким ускорением будут двигаться грузы, если их предоставить самим себе? Трением на оси блока пренебречь.

42. Вал массой m = 100 кг и радиусом R = 5 см вращается с частотой

ν = 8 с^-1. К цилиндрической поверхности вала прижали тормозную колодку с силой F = 40 Н, под действием которой вал остановился через время τ = 10 с. Определить момент и коэффициент силы трения.

43. За какое время t скатится без скольжения обруч с наклонной плоскости длиной l = 2 м и высотой h = 10 см?

44. Шар массой m = 10 кг и радиусом R = 20 см вращается вокруг оси, проходящей через его центр. Зависимость угла поворота от времени имеет вид

 φ = А + Bt² + Сt³ , где В = 4 рад/с², С = - 1 рад/с³. Найти закон изменения момента сил, действующего на шар. Определить момент сил спустя время

τ = 2 с после начала движения шара.

45. Тонкий однородный стержень длиной l = 50 см и массой m = 40 г вращается с угловым ускорением ε = 3 рад/с² вокруг горизонтальной оси, проходящей перпендикулярно стержню: 1) через его середину, 2) через один из его концов. Определить вращающий момент для этих случаев.

46. Два тела массами m₁ = 0,25 кг и m₂ = 0,15 кг связаны тонкой нитью, перекинутой через блок. Блок укреплен на краю горизонтального стола, по поверхности которого скользит тело массой m₁. С каким ускорением движутся тела? Коэффициент трения тела массой m₁ о поверхность стола

μ = 0,3. Масса блока m₀ = 0,1 кг, и ее можно считать равномерно распределенной по объему блока. Массой нити и трением в подшипниках оси блока пренебречь.

47. Через неподвижный блок массой m = 0,2 кг перекинут шнур, к концам которого подвесили грузы массами m₁ = 0,3 кг и m₂ = 0,5 кг. Определить силы натяжения шнура Т₁ и Т₂ по обе стороны блока во время движения грузов, если масса блока равномерно распределена по ободу.

48. Маховик в виде однородного диска массой m = 100 кг и радиусом

R = 40 см вращался с частотой n = 480 об/мин. Определить момент тормозящей силы, если после начала действия этой силы маховик остановился через время

τ = 80 с.

49. На шкив радиусом R = 10 см намотана нить, к концу которой привязан груз массой m = 2 кг. Груз опускается со скоростью, меняющейся по закону

 V = 2 – 8 t (м/с). Найти момент инерции шкива относительно оси вращения. Трением пренебречь.

50. Однородный сплошной цилиндр массой m₀ = 5 кг и радиусом

R = 20 см может без трения вращаться вокруг неподвижной горизонтальной оси. На цилиндр намотан тонкий нерастяжимый шнур, к которому прикреплён груз массой m₁ = 3 кг. Найти угловое ускорение цилиндра и расстояние, пройденное грузом массой m₁ за первые две секунды движения.

5l. При какой относительной скорости движения сокращение длины быстро движущегося тела составляет 25%?

52. Во сколько раз увеличится продолжительность существования нестабильной частицы (по часам неподвижного наблюдателя), если она будет

двигаться со скоростью, составляющей 99% скорости света?

53. Два встречных пучка электронов имеют относительно камеры ускорителя скорости, равные половине скорости света. Найти скорость одного пучка относительно другого.

 54. Ракета движется относительно неподвижного наблюдателя на Земле со скоростью 0,99с. Найти, как изменятся линейные размеры тел (по линии движения) и плотность вещества в ракете для неподвижного наблюдателя; какое время пройдет по часам неподвижного наблюдателя, если по часам, движущимся вместе с ракетой, прошел один год.

 55. Тело движется со скоростью 2·10³ м/с. Во сколько раз при этом увеличится плотность тела с точки зрения неподвижного наблюдателя?

 56. Найти скорость частицы, если ее кинетическая энергия составляет половину энергии покоя.

 57. Найти скорость космической частицы, если ее полная энергия в К раз превышает энергию покоя.

 58. Найти соотношение между полной энергией частицы Е, ее энергией покоя Е0 и импульсом.

59. Солнце излучает ежеминутно энергию Е = 2,4·10²⁸ Дж. Считая излучение Солнца стационарным, найти, за какое время масса Солнца уменьшится вдвое.

60. Какую скорость должно иметь движущееся тело, чтобы его продольные размеры уменьшились в два раза.

61. В баллоне объемом 10л находится гелий под давлением 10⁶ Н/м при 27⁰ С. После того, как из баллона было взято 10г. гелия, температура понизилась до 17⁰ С. Определить давление гелия, оставшегося в баллоне.

62. Смесь азота и гелия при температуре 27⁰C. Находится под давлением P=1,3·10² Па. Масса азота составляет 70% от общей массы смеси. Найти концентрацию молекул каждого из газов.

63. Найти среднюю квадратичную скорость, среднюю кинетическую энергию поступательного движения и среднюю полную кинетическую энергию молекул гелия и азота при 300⁰ К Определить полную энергию всех молекул l00 г каждого из газов.

64. Определить среднюю длину свободного пробега молекул, коэффициенты диффузии и вязкости азота при давлении 10 Па. И температуре 17⁰ К.

65. Определить плотность разряженного азота, если средняя длина свободного пробега молекул 10см. Какова концентрация молекул?

66. В сосуде емкостью 8,3л. Находится воздух при нормальном давлении и температуре 300⁰К. В сосуд вводят 3,6г. воды и закрывают крышкой. Определить давление в сосуде при 400⁰К., если вся вода при этой температуре превращается и пар.

67. Температура окиси азота (NО) 300⁰ К. Определить долю молекул, скорость которых лежит в интервале от 820 м/с до 830 м/с.

68. Сколько теплоты поглощают 200г. водорода, нагреваясь от 0⁰ до

100⁰ С. При постоянном давлении? Каков прирост внутренней энергии газа? Какую работу совершает газ?

69. Температура пара, поступающего в паровую, машину l27⁰ С., температура в конденсаторе 27⁰ С. Определить теоретически максимальную работу при затрате количества теплоты 42кДж. Какое количество теплоты было передано при этом газом холодильнику.

70. В цилиндре под поршнем находится водород массой 0,02 кг при

 300⁰ К. Водород сначала расширился адиабатически, увеличил свой объем в 5 раз, а затем был сжат изотермически, причем объем газа уменьшился тоже в 5 раз. Найти температуру в конце адиабатического расширения и работу, совершенную газом при этих процессах.

71. Найти изменение энтропии при нагревании 100 г воды от 0⁰ до 100⁰ С

и последующем превращении воды в пар при той же температуре.

72. Кислород, масса которого m=200 г, нагревают от 27⁰ С до 127⁰ С. Найти: изменение энтропии, если известно, что начальное и конечное давления одинаковы и близки к атмосферному.

73. В адиабатном процессе объем 2 молей двухатомного газа уменьшили в 2 раза, затем газ при постоянном объеме охладили до начальной температуры. Изобразить процессы на диаграмме рV. Определить изменение энтропии газа.

 74. Идеальный газ в количестве 2 молей сначала адиабатно сжимается так, что объем уменьшается в 3 раза, затем изотермически расширяется до начального объема. Изобразить процессы на диаграмме рV. Определить изменение энтропии газа.

 75. Идеальный газ в количестве 3 молей сначала изобарно уменьшает объем в 2 раз, затем изохорно увеличивает давление за счет нагревания в 2 раза. Изобразить процессы на диаграмме рV. Определить изменение энтропии газа.

76. В термосе смешивают горячую воду массой 1 кг при температуре 50 ºС

с холодной водой такой же массы при температуре 10 ºС. Определить приращение энтропии системы.

77. Кусок льда массой 100 г нагревают от температуры 250 К до температуры плавления и плавят. Определить приращение энтропии льда.

78. Водяной пар массой 100 г при температуре 100 °С превра­щается в воду, которая затем охлаждается до температуры 0 °С. Определить приращение энтропии.

79. Теплоизолированный сосуд разделен перегородкой на две части так, что объем одной из них в 2 раза больше другой. В меньшей части находилось 0,3 моля азота, а в большей части – 0,7 моля кислорода. Температуры газов были одинаковы. Перегородку убрали, и газы перемешались. Определить приращение энтропии системы.

80. Процесс расширения двух молей аргона происходит так, что давление увеличивается прямо пропорционально объему. Определить приращение энтропии газа при увеличении его объема в 2 раза.

 

ОСНОВЫ ЭЛЕКТРОДИНАМИКИ

 

ОСНОВНЫЕ ФОРМУЛЫ