С веществом
● Связь угла φ отклонения лучей призмой и преломляющего угла А призмы
φ = А (n – 1),
где n – показатель преломления призмы.
● Связь между показателем преломления и диэлектрической проницае-мостью вещества
n = 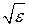 .
.
● Закон ослабления света в веществе (закон Бугера)
 ,
,
где I0 и I – интенсивности плоской монохроматической световой волны соответственно на входе и выходе слоя поглощающего вещества толщиной x; α – коэффициент поглощения.
● Эффект Доплера для электромагнитных волн в вакууме
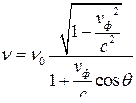 ,
,
где ν0 и νф – соответственно частоты электромагнитного излучения, испускаемого источником и воспринимаемого приемником; νф – скорость источника электромагнитного излучения относительно приемника; с – скорость света в вакууме; θ – угол между вектором скорости ν и направлением наблюдения, измеряемый в системе отсчета, связанной с наблюдателем.
● Поперечный эффект Доплера для электромагнитных волн в вакууме
(θ = π/2)
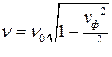 .
.
● Эффект Вавилова-Черенкова
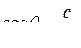 ,
,
где θ- угол между направлением распространения излучения и вектором скорости частицы; n- показатель преломления среды.
Поляризация света
● Степень поляризации света
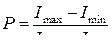 ,
,
где 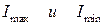 - соответственно максимальная и минимальная интенсивности частично поляризованного света, пропускаемого анализатором.
- соответственно максимальная и минимальная интенсивности частично поляризованного света, пропускаемого анализатором.
● Закон Малюса
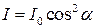 ,
,
где I – интенсивность плоскополяризованного света, прошедшего через анализатор; I0 - интенсивность плоскополяризованного света, падающего на анализатор; α – угол между плоскостью поляризации света и оптической осью поляризатора.
● Закон Брюстера
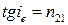
где 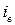 - угол падения, при котором отраженный от диэлектрика луч является полностью поляризованным;
- угол падения, при котором отраженный от диэлектрика луч является полностью поляризованным; 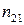 - относительный показатель преломления.
- относительный показатель преломления.
● Оптическая разность хода взаимно перпендикулярно составляющих плоскополяризованного света для пластинки в четверть длины волны
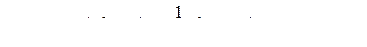 ,
,
где знак плюс соответствует отрицательным кристаллам, минус – положительным; λ0 – длина волны в вакууме.
● Угол поворота плоскости поляризации:
для оптически активных кристаллов и чистых жидкостей
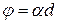 ;
;
для оптически активных растворов
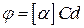 ,
,
где d – длина пути, пройденного светом в оптически активном веществе; 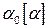 - удельное вращение; С – массовая концентрация оптически активного вещества в растворе.
- удельное вращение; С – массовая концентрация оптически активного вещества в растворе.
Квантовая природа излучения
● Закон Стефана-Больцмана
 ,
,
где 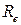 - энергетическая светимость (излучательность) черного тела; σ=5,67∙10-8 Вт/м2К4 – постоянная Стефана-Больцмана; Т- термодинамическая температура.
- энергетическая светимость (излучательность) черного тела; σ=5,67∙10-8 Вт/м2К4 – постоянная Стефана-Больцмана; Т- термодинамическая температура.
● Связь энергетической светимости 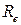 и спектральной плотности энергетической светимости
и спектральной плотности энергетической светимости 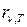 или
или 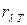 черного тела
черного тела
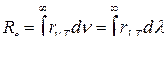 .
.
● Энергетическая светимость «серого» тела
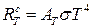 ,
,
где АТ – поглощательная способность «серого» тела.
● Закон смещения Вина
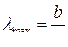 ,
,
где 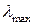 - длина волны, соответствующая максимальному значению спектральной плотности энергетической светимости черного тела; b=2,9∙10-3 м∙К - постоянная Вина.
- длина волны, соответствующая максимальному значению спектральной плотности энергетической светимости черного тела; b=2,9∙10-3 м∙К - постоянная Вина.
● Зависимость максимальной спектральной плотности энергетической светимости черного тела от температуры
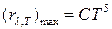 ,
,
где С=1,29∙10-5 Вт/(м3∙К5).
● Формула Релея-Джинса для спектральной плотности энергетической светимости черного тела
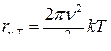 ,
,
где k- постоянная Больцмана.
● Энергия кванта
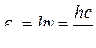 ,
,
где h=6,625∙10-34 Дж∙с – постоянная Планка.
● Формула Планка
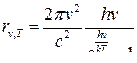
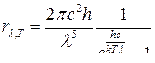 .
.
● Уравнение Эйнштейна для фотоэффекта
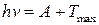 ,
,
где hν – энергия фотона, падающего на поверхность металла; Авых – работа выхода электрона из металла; 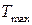 - максимальная кинетическая энергия фотоэлектрона.
- максимальная кинетическая энергия фотоэлектрона.
● «Красная граница» фотоэффекта для данного металла
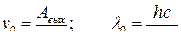 ,
,
где λ0 – максимальная длина волны излучения ( ν0 – соответственно минимальная частота), при которой фотоэффект еще возможен.
● Импульс фотона
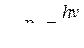 .
.
● Давление, производимое светом при нормальном падении на поверхность,
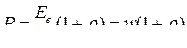 ,
,
где 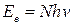 - облученность поверхности (энергия всех фотонов, падающих на единицу поверхности в единицу времени); ρ – коэффициент отражения;
- облученность поверхности (энергия всех фотонов, падающих на единицу поверхности в единицу времени); ρ – коэффициент отражения;
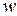 - объемная плотность энергии излучения.
- объемная плотность энергии излучения.
● Изменение длины волны рентгеновского излучения при комптоновском рассеянии
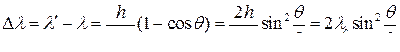 ,
,
где λ и λ′ - длина волн падающего и рассеянного излучений; m0 – масса электрона; θ – угол рассеяния; 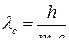 - комптоновская длина волны.
- комптоновская длина волны.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1. Математический маятник длиной l 1 =40 см и физический маятник в виде тонкого прямого стержня длиной l 2 =60 см синхронно колеблются около одной и той же горизонтальной оси. Определить расстояние a центра масс стержня от оси колебаний.
Решение:
При синхронном колебательном движении маятников их периоды равны 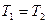 ,
,
где 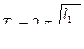
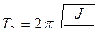 .
.
Отсюда
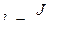 (1)
(1)
Момент инерции физического маятника определяется по теореме Штейнера:
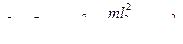 (2)
(2)
Подставив (2) в (1), получим квадратное уравнение
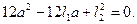 (3)
(3)
Из (3) найдем два корня: a 1 =10 см, a 2 =30 см.
Таким образом, при одном и том же периоде колебаний физического маятника возможны два варианта расположения оси.
Величину (1) называют приведенной длиной физического маятника.
Ответ: a1=10 см , a2=30 см .
Задача 2. В вакууме распространяется плоская электромагнитная волна. Амплитуда напряженности магнитного поля волны 0,1 А/м. Определить энергию, переносимую этой волной через поверхность площадью 1 м2, расположенную перпендикулярно направлению распространения волны, за время t = 1 с. Период волны T<< t.
Решение:
Плотность потока энергии электромагнитной волны определяется вектором Пойнтинга:
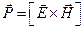 , где
, где 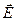 и
и 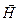 – векторы напряженности электромагнитного и магнитного полей. Учитывая, что векторы
– векторы напряженности электромагнитного и магнитного полей. Учитывая, что векторы 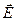 и
и 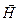 электромагнитной волны взаимно перпендикулярны, для модуля вектора p получим
электромагнитной волны взаимно перпендикулярны, для модуля вектора p получим
p = EH.
Так как величины E и H в каждой точке волны меняются со временем по гармоническому закону, находясь в одинаковых фазах, то мгновенное значение p равно
p = Em 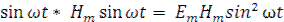
Энергия, переносимая через площадку S, перпендикулярную направлению распространения волны, в единицу времени,
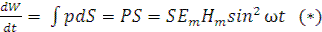
Учитывая, что в электромагнитной волне
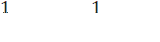
найдем:
Em = Hm 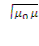
Тогда выражение (*) принимает вид
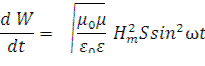
Энергия, переносимая волной за время t, равна
W = 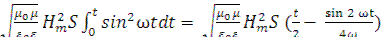
По условию T<< t, поэтому 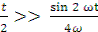 ; тогда
; тогда
W = 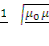
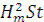
Подставляя числовые значения, получим
W = 
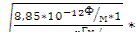 (0,1 А/м)2
(0,1 А/м)2  1 м2
1 м2  1 с = 1,88 Дж
1 с = 1,88 Дж
Ответ: W = 1,88 Дж.
Задача 3. Радиусы кривизны поверхностей линзы R1 = R2 = 20 см. Определить: а) фокусное расстояние линзы в воздухе; б) фокусное расстояние этой же линзы, погруженной в жидкость (nж = 1,7). Показатель преломления материала линзы nл = 1,5.
Решение:
Формула тонкой линзы
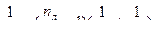
Применим данную формулу для случая (a), когда линза находится в воздухе, учитывая, что R1 = R2 = R
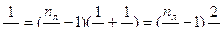
отсюда
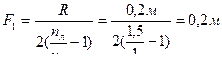
Для случая (б), когда линза погружена в жидкость
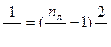
откуда
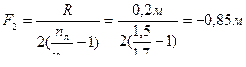
Ответ: F1 = 0,2 м; F2 = - 0,85 м
Задача 4. Установка для получения колец Ньютона освещается монохроматическим светом, падающим по нормали к поверхности пластинки. Наблюдение ведется в отраженном свете. Расстояние между вторым и двадцатым темными кольцами Δ τ2,20 = 4,8 мм
Найти расстояние между девятым и шестнадцатым темными кольцами Ньютона.
Решение:
Радиус темных колец в отраженном свете определяется формулой:
τR = 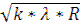 , где
, где
𝑘 – порядковый номер кольца;
λ – длина волны;
R – радиус кривизны линзы.
Отсюда
(1) Δ τ2,20 = 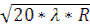 -
- 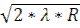 =
= 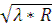 (
( 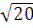 –
– 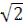 )
)
(2) Δ τ9,16 = 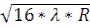 -
- 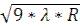 =
= 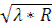 (
( 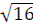 –
– 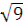 ) =
) = 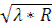
Из (1) имеем
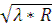 =
= 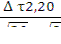 , подставим в (2)
, подставим в (2)
Δ τ9,16 = 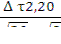 =
= 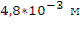 = 1,57
= 1,57 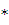 10 – 3 м
10 – 3 м
Ответ: Δ τ9,16 = 1,57 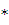 10 – 3 м = 1,57 мм
10 – 3 м = 1,57 мм
Задача 5. На дифракционную решетку нормально падает монохроматический свет. Определить угол дифракции для линии λ1 = 550 нм в четвертом порядке, если этот угол для линии λ2 = 600 нм в третьем порядке составляет 30˚.
Решение:
Формула дифракционной решетки для двух линий
dsinφ1 = 4 λ1 (1)
dsinφ2 = 3 λ2 (2)
Поделим уравнение (1) на уравнение (2) и получим
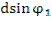 =
= 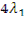 или
или 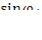 =
= 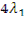
откуда sinφ1 = 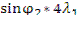 =
= 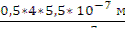 = 0,61
= 0,61
φ1 = arcsin 0,61 = 37˚42΄
Ответ: φ1 = 37˚42΄
Задача 6. Найдите угол полной поляризации (iБр) при отражении света от стекла (nc = 1,57), помещенного в воду (nв = 1,33). Определить скорость света в воде.
Решение:
Согласно закону Брюстера tg iБр = 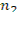 при этом n1 = nв; n2 = nс
при этом n1 = nв; n2 = nс
Тогда tg iБр = 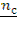 = 1,18, следовательно, iБр = arctg 1,18 ≈ 50˚
= 1,18, следовательно, iБр = arctg 1,18 ≈ 50˚
Абсолютный показатель преломления среды n =  , тогда, зная nв, найдем скорость распространения света в воде: V =
, тогда, зная nв, найдем скорость распространения света в воде: V = 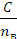 =
= 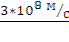 = 2,26
= 2,26 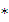 108
108 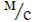
Ответ: iБр ≈ 50˚; V = 2,26 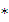 108
108 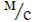
Задача 7. Температура внутренней поверхности электрической печи
T = 700˚C. Определите мощность излучения печи через небольшое отверстие диаметром d = 5 см, рассматривая его как излучение абсолютно черного тела.
Решение:
Из закона Стефана – Больцмана энергетическая светимость (излучательность) черного тела R = σ 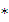 T 4. Другой стороны, N = R
T 4. Другой стороны, N = R 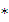 S, где S – площадь отверстия.
S, где S – площадь отверстия.
S = П 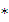 τ 2 = П (
τ 2 = П ( 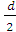 ) 2 =
) 2 = 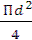 , подставим
, подставим
N = R  S = σ
S = σ  T 4 *
T 4 * 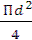 =
= 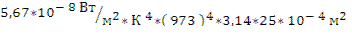 = 9,97
= 9,97 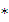 101 = 99,7 Вт
101 = 99,7 Вт
Ответ: N = 99,7 Вт
Задача 8. Красная граница фотоэффекта для металла λк = 6,2 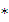 10 – 5 см. Найти величину запирающего напряжения для фотоэлектронов при освещении металла светом длиной волны λ = 330 нм.
10 – 5 см. Найти величину запирающего напряжения для фотоэлектронов при освещении металла светом длиной волны λ = 330 нм.
Решение:
Запирающее напряжение – это напряжение на электродах, способное остановить электроны, вылетевшие из металла. Следовательно, работа сил электрического поля Аэ равна кинетической энергии фотоэлектронов. Аэ = Ек или е 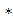 U = Ек. Кинетическую энергию определяем из уравнения Эйнштейна.
U = Ек. Кинетическую энергию определяем из уравнения Эйнштейна.
hν = Aвых + Ек => Eк = hν - Aвых
Если известна красная граница фотоэффекта, то работа выхода определяется из выражения Aвых = h 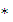 νк = h
νк = h 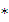
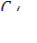
Подставим е 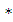 U = h
U = h 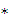
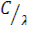 - h
- h 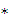
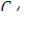 = h
= h 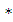 C
C 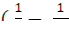 )
)
откуда U = 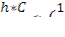 -
- 
U = 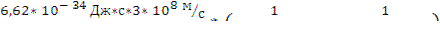 = 1,76 В
= 1,76 В
Ответ: U = 1,76 В
КОНТРОЛЬНАЯ РАБОТА № 3
1. Точка совершает гармонические колебания по закону x=Asinωt. В некоторый момент времени ее смещение равно 5 см. При увеличении фазы вдвое смещение стало 8 см. Найти амплитуду колебаний.
2. Определить максимальное ускорение amax материальной точки, совершающей гармонические колебания с амплитудой A=25 см, если наибольшая скорость точки Vmax=0,5 м/с. Записать также уравнение колебаний.
3. На стержне длиной l = 30 см и массой m = 1 кг, закреплены два одинаковых грузика: один - в середине стержня, другой - на одном из его концов. Эта система может свободно вращаться около горизонтальной оси, проходящей через свободный конец стержня. Определять период собственных колебаний T этого физического маятника.
4. Диск радиусом R = 20 см может свободно вращаться вокруг горизонтальной оси, проходящей через середину радиуса перпендикулярно его плоскости. Определить частоту n собственных колебаний этого физического маятника.
5. Однородный стержень массой m и длиной l может свободно вращаться вокруг горизонтальной оси, проходящей через его конец. Определить частоту собственных колебаний стержня.
6. Однородный стержень массой m, длиной l может свободно вращаться вокруг горизонтальной оси, проходящей на расстоянии l/4 от одного из его концов. Определить период колебаний этого физического маятника.
7. На горизонтальном столе лежит шар массой 200 г, прикрепленный к горизонтально расположенной пружине жесткостью 500 Н/м. В шар попадает пуля массой 10 г, летящая горизонтально со скоростью 300 м/с, и застревает в нем. Определить амплитуду и период колебаний шара. Перемещением шара во время удара, сопротивлением воздуха и трением между поверхностью шара и стола пренебречь.
8. Однородный стержень массой 0,5 кг и длиной l м может свободно вращаться вокруг горизонтальной оси, проходящей через один из его концов. В противоположный конец стержня попадает пуля массой 10 г, летящая горизонтально со скоростью 300 м/с, и застревает в нем. Определить амплитуду и период колебаний стержня.
9. Однородный стержень может вращаться вокруг горизонтальной оси, проходящей на расстоянии 1/4 от одного из его концов. В противоположный конец попадает пуля массой 10 г, летящая горизонтально со скоростью
200 м/с, и застревает в нем. Определить амплитуду и период колебаний стержня. Масса стержня 0,5 кг, длина 1 м.
10. Лифт, в котором колеблется математический маятник, опускается с ускорением a = 3 м/с2. Определить период колебаний T маятника. Его длина равна 1 м.
11. Какова емкость в колебательном контуре с индуктивностью 50 мГн, если частота контура 1 кГц?
12. Плоский конденсатор с площадью пластин 100 см2, разделенных слоем парафинированной бумаги толщиной 0,01 мм, и катушка образуют колебательный контур. Частота колебаний в контуре 1 кГц. Какова индуктивность катушки?
13. Колебательный контур состоит из конденсатора емкостью 1 нФ и катушки индуктивностью 5 мГн. Логарифмический декремент колебаний равен 0,005. Определить время, в течение которого контур потеряет 99% своей энергии, и среднее значение энергии, теряемой за один период, если максимальная разность потенциалов на обкладках конденсатора равна 6 В.
14. Колебательный контур состоит из конденсатора ёмкостью 7 мкФ и катушки индуктивностью 0,23 Гн с сопротивлением 40 Ом. Найти период колебаний и логарифмический декремент.
15. Сила тока в колебательном контуре изменяется по закону i=0,1cos2πt. Найти индуктивность контура, если максимальная энергия электрического поля конденсатора равна 10 мДж.
16. Максимальная энергия магнитного поля колебательного контура
1 мДж при силе тока 0,8 А. Чему равна частота колебаний контура, если максимальная разность потенциалов на обкладках конденсатора 1200В? Чему равны индуктивность и емкость контура, период колебаний?
17. В колебательном контуре с периодом T = 10-5 с напряжение на конденсаторе в момент времени t = 2,5.10-6 с (считая от напряжения U = 0) составляет 500 В. Найти емкость конденсатора при общей энергии контура W = 1 мДж.
18. На какую длину волны λ будет резонировать контур, состоящий из катушки индуктивностью L=4 мкГн и конденсатора электроемкостью
C=1,11 нФ?
19. Катушка индуктивностью L=1 мГн и воздушный конденсатор, состоящий из двух круглых пластин диаметром D=20 см каждая, соединены параллельно. Расстояние d между пластинами равно 1 см. Определить период T колебаний.
20. Индуктивность L колебательного контура равна 0,5 мГн. Какова должна быть электроемкость C контура, чтобы он резонировал на длину волны λ=300 м?
21. Двояковыпуклая линза, оптическая сила которой D=8 Дптр., даёт изображение предмета на экране, удалённом на расстоянии L=75 см., размером
h= 10см. Определить положение и высоту предмета.
22. Светящий предмет находится на расстоянии L=4,2 м от экрана. Где надо поместить собирающую линзу, чтобы получить 20-ти кратное увеличение предмета? Найти оптическую силу линзы.
23. Фокусное расстояние линзы F1=0,5 м. Найти фокусное расстояние линзы F2, погруженной в воду, если показатель преломления стекла, из которого сделана линза, n=1,6.
24. Линза изготовлена из стекла, показатель преломления которого для красных лучей равен 1,5, для фиолетовых 1,52. Радиусы кривизны обеих поверхностей линзы одинаковы и равны 1м. Определить отношение фокусного расстояния линзы для красных лучей к фокусному расстоянию для фиолетовых.
25. Луч света выходит из скипидара в воздух. Предельный угол полного внутреннего отражения для этого луча 420 23/ . Чему равна скорость распространения света в скипидаре?
26. Вогнутое сферическое зеркало дает на экране изображение предмета, увеличенное в Г=4 раза. Расстояние а от предмета до зеркала равно 25 см. Определить радиус R кривизны зеркала.
27. Если расстояние предмета от линзы f1=36 см, то высота изображения
h1=5 см, если же это расстояние f2=24 см, то высота изображения h2=10 см. Определить фокусное расстояние линзы.
28. Тонкая стеклянная линза имеет оптическую силу D=5 Дптр. Та же линза, погруженная в жидкость, имеет оптическую силу D1=-1 Дптр. Найти показатель преломления жидкости, зная, что показатель преломления стекла равен 1,5.
29. Предельный угол полного внутреннего отражения для луча, выходящего из некоторой жидкости, равен α=550. Найти скорость распространения света в этой жидкости?
30. Луч света переходит из стекла (nс=1,5) в воздух, падая на стеклянную поверхность под углом: 1) φ1=420 ; 2) φ2=600. Найти углы преломления в каждом случае.
31. На диафрагму с двумя щелями, находящимися на расстоянии 2 мм, падает нормально монохроматический свет. На экране, отстоящем от диафрагмы на расстоянии 129 см, наблюдаются интерференционные полосы. На какое расстояние сместятся полосы, если одну щель закрыть стеклянной пластинкой толщиной
11 мкм? Показатель преломления стекла 1,86.
32. Расстояние между двумя щелями в опыте Юнга равно 967 мкм, щели удалены от экрана на расстояние 363 см. Определить длину волны, испускаемую источником монохроматического света, если ширина 8 полос интерференции на экране равна 1,6 см.
33. На стеклянную пластику нанесен тонкий слой прозрачного вещества с коэффициентом преломления n=1,6. Пластина освещена параллельным пучком монохроматического света с длиной волны λ=640 нм, падающим на пластинку нормально. Какую минимальную толщину d должен иметь слой, чтобы отраженный пучок имел наименьшую яркость?
34. На поверхности воды находится тонкая пленка скипидара (n=1,48) толщиной 0,25 мкм. Какого цвета представится пленка при наблюдении ее в отраженном свете под углом 60 градусов?
35. Расстояние между двумя когерентными источниками 0,9 мм, а расстояние от источников до экрана 1,5 м. Источники испускают монохроматический свет с длиной волны 0,6 мкм. Определить число интерференционных полос, приходящихся на 1 см экрана.
36. На тонкий стеклянный клин падает нормально монохроматический свет. Наименьшая толщина клина, с которой видны интерференционные полосы в отраженном свете, равна 0,12 мкм. Расстояние между полосами
0,6 мм. Найти угол между поверхностями клина и длину волны света, если показатель преломления стекла 1,5.
37. Тонкая пленка с показателем преломления 1,5 освещается рассеянным светом с длиной волны 600 нм. При какой минимальной толщине пленки исчезнут интерференционные полосы?
38. Две плоскопараллельные стеклянные пластинки приложены одна к другой так, что между ними образовался воздушный клин с углом 37 секунд. На одну из пластин падает нормально монохроматический свет с длиной волны 417 нм. На каком (в мм) расстоянии от линии соприкосновения наблюдается первая светлая полоса в отраженном свете?
39. Для наблюдения колец Ньютона в отраженном свете используется стеклянная пластинка, на которую положена выпуклой стороной плосковыпуклая линза. Монохроматический свет падает нормально. Радиус линзы 8,6 м. Измерениями установлено, что диаметр четвертого темного кольца равен 9 мм. Определить длину волны падающего света.
40. Найти показатель преломления жидкости, заполняющей пространство между стеклянной пластинкой и лежащей на ней плосковыпуклой линзой, если при наблюдении в отраженном свете радиус 7-го темного кольца Ньютона оказался равным 2,825 мм. Радиус кривизны выпуклой поверхности линзы равен 299 см. Установка освещается светом с длиной волны 699 нм.
41. На узкую щель нормально падает излучение длиной волны 441 нм. Дифракционная картина, даваемая щелью, наблюдается на экране с помощью линзы с фокусным расстоянием 234 см. Определить ширину щели, если расстояние между серединами полос спектров 1-го и 2-го порядка на экране равно 42 мм. Из-за малости углов синусы считать равными тангенсам.
42. На щель падает нормально параллельный пучок монохроматического света с длиной волны λ. Ширина щели 6λ. Под каким углом будет наблюдаться 3-ий дифракционный минимум света? Третий дифракционный максимум света?
43. В спектре, полученном с помощью дифракционной решетки, спектральную линию наблюдают в первом порядке под углом 8,36 град. Определить наивысший порядок спектра, в котором можно наблюдать эту линию с помощью той же дифракционной решетки, если свет падает на решетку нормально к ее поверхности.
44. Постоянная дифракционной решетки равна 10-2 мм. Решетка освещается монохроматическим светом длиной волны 0,5 мкм. Под каким
(в градусах) углом наблюдается десятый дифракционный максимум?
45. На дифракционную решетку, содержащую 218 штрихов на миллиметр, падает нормально белый свет. Спектр проектируется линзой, помещенной вблизи решетки, на экран, расположенный на расстоянии 209 см от линзы. Границы видимого спектра 400-780 нм. Определить длину спектра 1-го порядка на экране. Указание: синусы углов дифракции считать равным тангенсом.
46. На дифракционную решетку с постоянной 6 мкм падает нормально монохроматический свет. Угол между спектрами 7-го и 8-го порядков равен 17 градусов. Определить длину волны. Ответ дать в нанометрах.
47. Период дифракционной решетки 6 мкм. Ширина прозрачной части
4 мкм. Сколько главных максимумов будет наблюдаться в спектре по одну сторону от нулевого максимума до угла 76 градусов? Длина световой волны равна 434 нм.
48. Период дифракционной решетки равен 7 мкм. Для спектральной линии водорода с длиной волны 486 нм подобрать такой наибольший интервал длин волн, чтобы нигде не было перекрытия спектров при освещении светом в заданном интервале. Ширина дифракционной решетки
3 см. Ответ дать в нанометрах.
49. Узкий пучок рентгеновских лучей падает под углом скольжения
20 градусов на дифракционную решетку с периодом 2,0 мкм. Первый дифракционный максимум наблюдается под углом 12 минут. Определить длину рентгеновских лучей в нанометрах.
50. Дифракционная решетка содержит 200 штрихов на 1 мм. На решетку падает нормально монохроматический свет (λ=0,55 мкм). Максимум какого наибольшего порядка дает эта решетка?
51. Частично поляризованный свет проходит через поляроид. При повороте поляроида на 60 град. от положения, соответствующего максимальной яркости, яркость пучка уменьшается в 2 раза. Учитывая, что поляроид поглощает 10% проходящей через него энергии, определить степень поляризации света, падающего на поляроид.
52. Между двумя параллельными поляроидами помещают кварцевую пластинку толщиной 1 мм, вырезанную параллельно оптической оси. При этом плоскость поляризации монохроматического света, падающего на поляризатор, повернулась на угол 20 град. При какой (в мм) минимальной толщине пластинки свет не пройдет через анализатор?
53. Пучок естественного света падает на пластину из 6 николей, плоскость пропускания каждого из которых повернута на угол 30° относительно плоскости пропускания предыдущего николя. Какая часть светового потока проходит через систему?
54. Естественный свет пропускают через два одинаковых поставленных один за другим несовершенных поляризатора. Интенсивность прошедшего через эту систему света при параллельных плоскостях поляризаторов (III) превышает интенсивность при взаимно перпендикулярных плоскостях (I⊥) в 9,53 раза. Определить: а) степень поляризации света, прошедшего только через один из поляризаторов; б) степень поляризации, обуславливаемую системой при параллельных плоскостях поляризаторов.
55. Если между скрещенными поляроидами поместить третий, оптическая ось которого составляет угол α=15° с оптической осью анализатора, то поле зрения просветлеет. Какая часть светового потока падающего естественного света проходит через эту систему?
56. Угол α между плоскостями пропускания поляроидов равен 50°. Естественный свет, проходя через такую систему, ослабляется в n=8 раз. Пренебрегая потерей света при отражении, определить коэффициент поглощения света k в поляроидах.
57. Найти угол φ между главными плоскостями поляризатора и анализатора, если интенсивность естественного света, проходящего через поляризатор и анализатор, уменьшается в 4 раза.
58. Чему равен угол между главными плоскостями двух поляризаторов, если интенсивность света, прошедшего через них, уменьшилась в 5,3 раза? Считать, что каждый поляризатор отражает и поглощает 13% падающего на них света.
59. Концентрация раствора сахара, налитого в стеклянную трубку,
C1=0,3 г/см3. Этот раствор вращает плоскость поляризации монохроматического света на угол φ1=25°. Определить концентрацию C2 в другой такой же трубке, если он вращает плоскость поляризации на угол φ2=20°.
60. Чему равен показатель преломления стекла, если при отражении от него света отражённый луч будет полностью поляризован при угле 300.
61. Электрическая печь потребляет мощность P=500 Вт. Температура ее внутренней поверхности при открытом небольшом отверстии диаметром
d=5 см равна 700°C. Какая часть потребленной мощности рассеивается стенками?
62. Известно, что температура поверхности Солнца 5800 K. На какую длину волны приходится максимум лучеиспускательной способности Солнца? Считать Солнце абсолютно черным телом. Ответ дать в мкм.
63. Определить длину волны, отвечающую максимуму испускательной способности черного тела при температуре 37°C и энергетическую светимость тела.
64. При какой температуре интегральная светимость поверхности серого тела с коэффициентом поглощения 0,0625 равна энергетической светимости абсолютно черного тела, имеющего температуру 1000 K?
65. Энергетическая светимость абсолютно черного тела равна 50 Вт/см2. Определите длину волны, соответствующую максимуму испускательной способности.
66. Энергетическая светимость абсолютно черного тела равна 3 Вт/см2. Определить длину волны, отвечающую максимуму спектральной плотности энергетической светимости этого тела.
67. Абсолютно черное тело находится при температуре T1=2900К. В результате остывания этого тела длина волны, на которую приходится максимум энергетической светимости, изменилась на Δλ=9 мкм. До какой температуры охладилось тело?
68. Мощность изучения шара радиусом 10 см при некоторой температуре равна 1 кВт. Найти эту температуру, считая шар серым телом с коэффициентом поглощения 0,25.
69. Определить поглощательную способность AT серого тела, для которого температура, измеренная радиационным пирометром Tp=1,4 кК, тогда как истинная температура T тела равна 3,2 кК.
70. Определить поглощательную способность поверхности серого тела, если известно, что нагретая до температуры T=2500 K поверхность площадью S=10 см2 излучает в 1 секунду Фэ=6,7·102 Дж энергии.
71. Тающая льдинка массой 0,1 г при освещении светом с длиной волны
0,1 мкм поглощает 1018 фотонов в секунду. Через какой промежуток времени льдинка растает?
72. Определить длину волны излучения, импульс фотона которого равен импульсу электрона, обладающего скоростью 10 Мм/с. Ответ дать в пикометрах.
73. Определить энергию и импульс фотонов, соответствующих наиболее длинным (длина волны равна 0,76 мкм) и наиболее коротким (длина волны равна 0,4 мкм) волнам видимой части спектра.
74. Определите длину волны фотона с импульсом, равным импульсу электрона, прошедшего из состояния покоя ускоряющую разность потенциалов 5 В.
75. Свет, падая на зеркальную поверхность, оказывает давление 10 мкПа. Определить энергию света, падающего на площадь 1 м2 за 1 с.
76. Давление света с длиной волны 0,6 мкм, падающего нормально на черную поверхность, равно 1 мкПа. Определить число фотонов, падающих за секунду на
1 см2 этой поверхности.
77. Поверхность площадью S=100 см2 каждую минуту получает 63 Дж световой энергии. Найти световое давление р в случае, когда поверхность: а) полностью отражает все лучи и б) полностью поглощает все падающие на нее лучи.
78. Давление света с длиной волны 40 нм, падающего нормально на чёрную поверхность, равно 2 нПа. Определить число фотонов, падающих за 10 с на 1 мм2 этой поверхности.
79. На идеально отражающую поверхность площадью 5 см2 за время
3 мин нормально падает монохроматический свет, энергия которого 9 Дж. Определить световое давление, оказываемое на поверхность.
80. Для прекращения тока фотоэмиссии из платины необходима задерживающая разность потенциалов 3,7 В. При облучении теми же фотонами другого металла, задерживающая разность потенциалов равна 6 B. Найти работу выхода электрона с поверхности этого металла, если для платины работа выхода равна 6,3 эВ. Ответ дать в электрон-вольтах.
Дата: 2018-12-28, просмотров: 773.