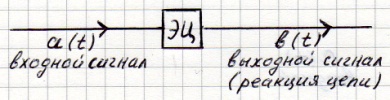
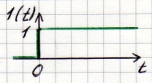
Реакция цепи на единичную функцию 1(t), называемую функцией Хэвисайда, называется переходной характеристикой цепи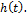 
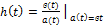
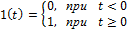
Входной сигнал - может быть напряжением (током).
Выходной сигнал – либо ток, либо напряжение на элементах.
Переходные характеристики численно равны току или напряжению на соответствующих элементах.
RL – цепь: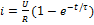 
; 
; 
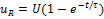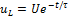
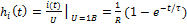
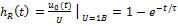
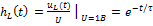
RC – цепь: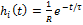 
; 
; 
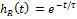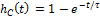
Интеграл Дюамеля можно определить при произведении входных сигналов.
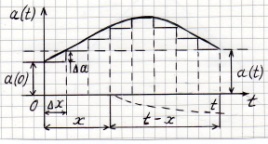Пусть 
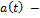непрерывно изменяющаяся функция.
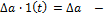запишем входной сигнал из этих сигналов 
,
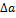идущих друг за другом непрерывно с одинаковым интервалом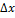 
.
Каждый скачок запаздывает на 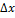, т.е. действует в момент 
.
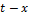Элементарные скачки имеют знак «+» для возрастающей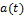 
, «-» - для убывающей.
Реакция цепи:
1) При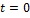 
действует скачок 
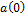и реакция цепи будет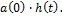 
2) При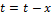 
скачок 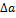и реакция цепи: 
.
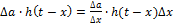3) Скачки включаются непрерывно от 
до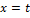 
и суммарная реакция цепи:
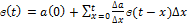
4) 
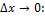
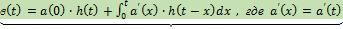
Интеграл Дюамеля
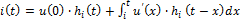
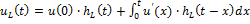
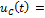
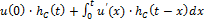
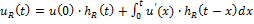
Примечание: интеграл Дюамеля применим также для входного сигнала, представляющего собой
кусочно-аналитическую функцию.
Задача:
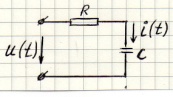
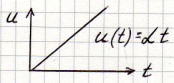Определить: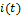 
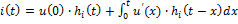
, где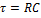 
; 
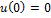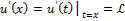
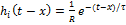
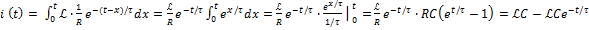
Глава 8. Операторный и спектральный анализ цепи.
Операторный метод расчетов переходных процессов
8.1.1. Метод преобразований по Лапласу.
Недостатком классического метода является сложность решения дифференциальных уравнений 2-ого порядка и выше.
Преимущество операторного метода простота записи начальных условий. Они сразу обозначаются на схеме и учитываются при расчете.
Суть метода:
1) 
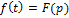
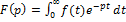, где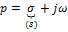 
2) Идет расчет цепи в операторной форме: при этом упрощаются операции интегрирования и дифференцирования. Вместо дифференциальных уравнений решаются алгебраические, интегрированные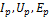 
3) Обратно по времени:
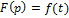
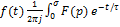
Изображение некоторых функций по Лапласу
1) 
, 
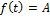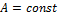
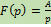
2) 
, 
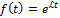
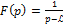
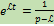
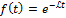
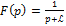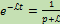
3) 
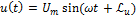
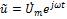, где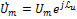 
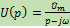
Пример: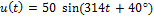 
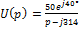
4) Выражение функций, связанных интегрированием и дифференцированием.
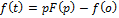
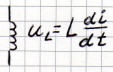
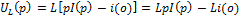(1)
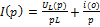(2)
При начальных условиях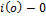 
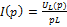
Заметим, что в этом методе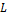 
заменяется на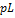 
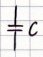
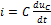
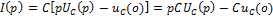(3)
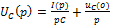(4)
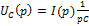
Заменяем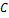 
на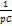 
Аналогичные выражения получатся при интегрировании.
Закон Ома в операторной форме.
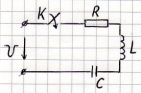
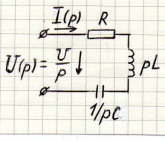
1) При нулевых начальных условиях:
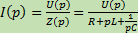
2) Ненулевые начальные условия:
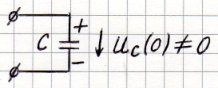
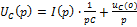
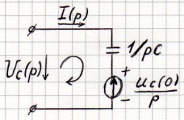
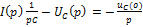
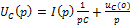
Если ненулевые начальные условия, то добавляем
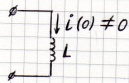
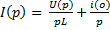
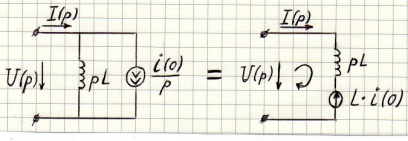
2 закон Кирхгофа для этой схемы: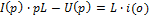 
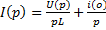
Общий случай закона Ома:
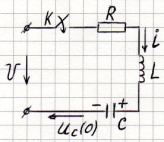
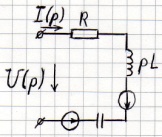
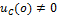
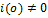
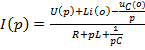
Законы Кирхгофа в операторной форме.
1з.К.: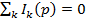 
2з.К.: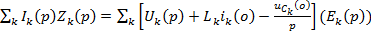 
При нулевых начальных условиях: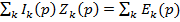 
Дата: 2018-12-28, просмотров: 255.
