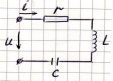
Дано: 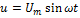
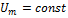
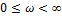
Частотная характеристика (ЧХ) – зависимость какого-то параметра от частоты.
1) ЧХ сопротивлений:
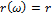 - активное сопротивление
- активное сопротивление
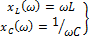 - активные
- активные
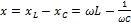 - реактивное
- реактивное
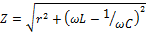
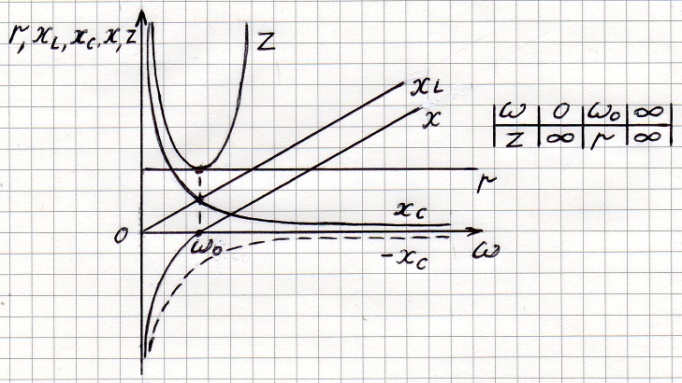
2) ЧХ тока: 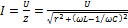
| 𝜔 | 0 | 0<𝜔< 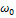
| 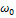
| 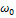 <𝜔<∞ <𝜔<∞
| ∞ |
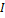
| 0 | ↑ емкостной характер сопротивления | 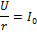
| ↓ индуктивный характер сопротивления | 0 |
3) Фаза ЧХ. Зависимость фазы от частоты 𝜑(𝜔)
| 𝜔 | 0 | 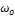
| ∞ |
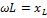
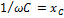
| 0 ∞ | 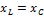
| ∞ 0 |
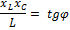
|  ∞ ∞
| 0 | ∞ |
| 𝜑 | 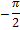
| 0 | 
|
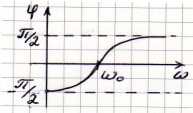
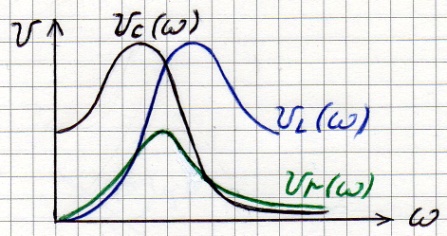
4)
5) ЧХ в относительных единицах:
Вид, рассмотренных ранее ЧХ, зависит от параметров в цепи r , L , C или от добротности.
ЧХ в относительных единицах универсальны, т.к. пригодны для цепей с различными параметрами.
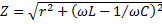 = (разделим и умножим на
= (разделим и умножим на 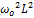 =
=
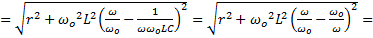
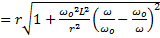 , где
, где 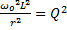
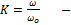
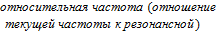
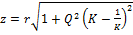
6) ЧХ сопротивления в относительных единицах:
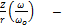

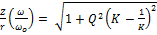
При 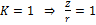
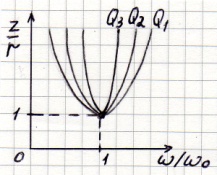
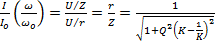
При 
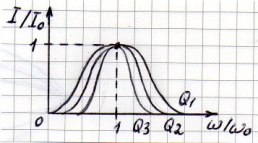
Полоса пропускания колебательного контура.
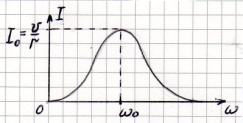
Частотная характеристика (ЧХ) тока показывает, что контур обладает избирательными свойствами (цепь обладает наименьшим сопротивлением для тока той частоты, которая наиболее близка к резонансной). Чем больше Q , тем острее резонансная кривая тока и выше ее избирательные свойства.
Полосой пропускания контура называют полосу частот вблизи резонансной частоты, на границах которой ток снижается до значения:
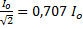
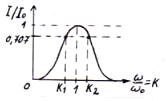
Точки пересечения определяют полосу частот
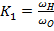
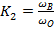
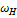 и
и 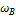 - нижнее и верхнее граничные частоты полосы пропускания.
- нижнее и верхнее граничные частоты полосы пропускания.
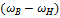 - абсолютная полоса пропускания
- абсолютная полоса пропускания
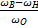 - относительная полоса пропускания
- относительная полоса пропускания
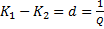 , где
, где 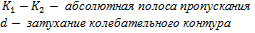
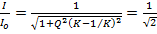 ⇒ -
⇒ - 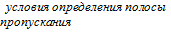
⇒ 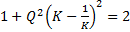
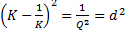
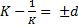
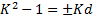
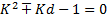
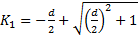
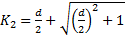
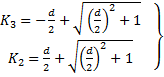 - отбрасываем
- отбрасываем

Что и требовалось доказать.
Глава 6. Расчет индуктивно связанных, трехфазных и четырех полюсных цепей.
Индуктивно связанные цепи.
6.1.1. Основные определения.
Индуктивно связанными называются цепи, в которых есть магнитные потоки, сцепленные с цепями 2-ух и более катушек (трансформатор, связанные контуры в радиоприемнике).
В таких цепях, существование тока в одной катушке, приводит к появлению в другой индуктивно связанной катушки, ЭДС которой называется ЭДС взаимоиндукции.
①
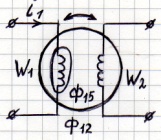
← концы разомкнуты
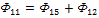 , где
, где
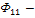 поток самоиндукции 1-ой катушки
поток самоиндукции 1-ой катушки
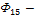 поток рассеяния (охватывает 1-ую катушку)
поток рассеяния (охватывает 1-ую катушку)
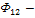 поток взаимной индукции (охватывает обе катушки) – рабочий поток
поток взаимной индукции (охватывает обе катушки) – рабочий поток
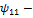 поток сцепления 1-ой катушки
поток сцепления 1-ой катушки
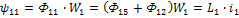
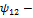 поток сцепления 2-ой катушки
поток сцепления 2-ой катушки
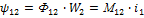 , где
, где 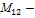
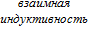
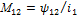
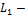 индуктивность
индуктивность 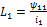
②
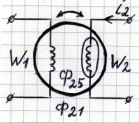
← концы разомкнуты
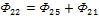
Аналогично:
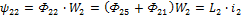
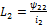
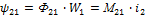
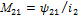
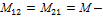 для линейных цепей
для линейных цепей
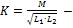 коэффициент связи ,
коэффициент связи , 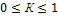
Если К = 0 , общего магнитного потока у катушек нет:
1) удаленные друг от друга катушки;
2) катушки, разделенные магнитным экраном;
3) катушки, оси которых перпендикулярны.
Если К = 1 , катушки пронизаны одним и тем же магнитным потоком (поток рассеяния отсутствует). Может быть при совмещении катушек (бифилярная намотка).
 ③
③
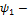 общее потокосцепление 1-ой катушки
общее потокосцепление 1-ой катушки
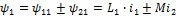
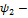 общее потокосцепление 2-ой катушки
общее потокосцепление 2-ой катушки
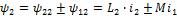
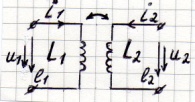
Знаки слагаемых зависят от направления магнитных потоков, а последние зависят от направления тока и намотки катушки.
В ОТЦ на электрических схемах направление намотки не показывают, а помечают одинаковыми значками одноименные выводы катушек (начало или концы обмоток).
Направление токов в каждой из катушек выбирают произвольно.
2 варианта:
1) согласное включение катушек (относительно одноименных зажимов), согласно включению:
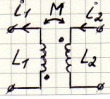
⊕ магнитные потоки складываются
2) встречное включение катушек:
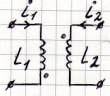
⊝ разность магнитных потоков
По закону электромагнитной индукции:
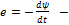 ЭДС
ЭДС
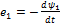
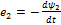
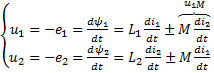 (2)
(2)
Уравнения (2) показывают, что если катушки 1 и 2 связаны через взаимоиндукцию М, то в 1-ую катушку вносится напряжение 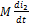 , обусловленное током 2-ой катушки.
, обусловленное током 2-ой катушки.
Аналогично для 2-ой катушки.
Дата: 2018-12-28, просмотров: 409.