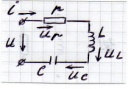
5.1.1. Резонанс напряжений (последовательный резонанс).
 Дано:
Дано: 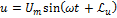
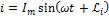
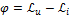
 , L, C
, L, C
Резонансом напряжений называют такой режим работы цепи с последовательным соединением  , L, C – элементов, когда ток совпадает по фазе с приложенным к цепи напряжением.
, L, C – элементов, когда ток совпадает по фазе с приложенным к цепи напряжением.
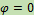 - условие возникновения резонанса
- условие возникновения резонанса
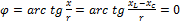
или 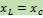 , или
, или 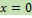
Частота, при которой выполняется условие 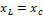 , называется резонансной частотой.
, называется резонансной частотой.
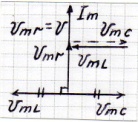
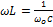 ⇒
⇒ 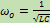
Особенности работы цепи при резонансном напряжении.
1) 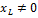 ;
; 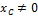 , но
, но 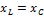 и
и 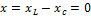
2) 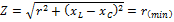 - минимально
- минимально
3) 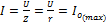 - максимальный
- максимальный
4) Т.к. 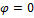 , то
, то 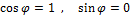 .
.
Потребляется только активная мощность:
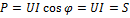 ;
; 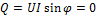
5) 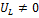 ;
;  , но
, но 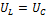 и
и 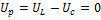
6) 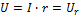
7) 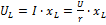 ;
; 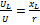
Если 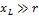 , то
, то 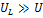
8) 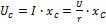
аналогично ⇒ если 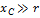 , то
, то 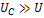
Характеристическое (волновое) сопротивление, добротность и затухание контура:
Цепи, в которых возникает резонанс, в радиотехнике называются колебательными контурами.
Последовательный колебательный контур:
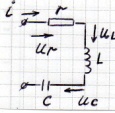
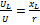
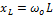 - при резонансе
- при резонансе
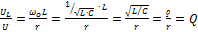
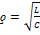 [Ом] - характеристическое сопротивление цепи
[Ом] - характеристическое сопротивление цепи
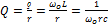 - добротность колебательного контура
- добротность колебательного контура
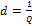 - затухание колебательного контура
- затухание колебательного контура
Энергия колебательного контура при резонансном напряжении.
( 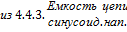 ):
): 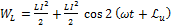
( 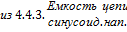 ):
): 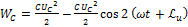
При резонансе напряжений максимум энергии магнитного поля напряженности, индуктивности и емкости равны.
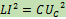 (*)
(*)
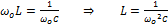
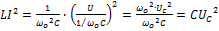
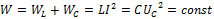
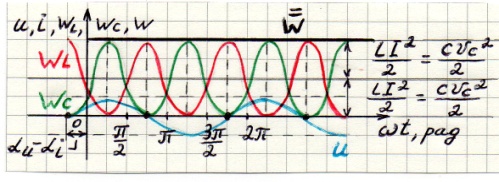
Если 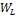 или
или 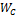 сложить с
сложить с 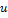 , то получится постоянная
, то получится постоянная 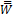 .
.
В момент, когда 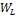 достигает max -
достигает max - 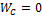 и наоборот.
и наоборот.
Таким образом, при резонансе происходит обмен энергиями между реактивными элементами и называется колебательным контуром. Энергия одного элемента переходит к другому элементу, причем суммарно энергия остается неизменной. При резонансе происходит непрерывное перераспределение или колебание энергии электрических и магнитных полей. Энергия, которая поступает от источника, выделяется в виде тепла на активном сопротивлении. Отсюда название «колебательный контур».
5.1.2. Резонанс токов (параллельный резонанс).
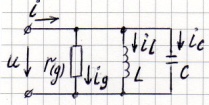
Резонансом токов называют такой режим работы цепи с параллельным соединением  , L, C , когда ток в неразветвленной части цепи совпадает по фазе с приложенным к цепи напряжением.
, L, C , когда ток в неразветвленной части цепи совпадает по фазе с приложенным к цепи напряжением.
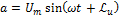 ;
; 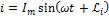 ;
; 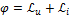
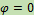 - условие возникновения резонанса
- условие возникновения резонанса
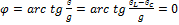 ;
; 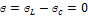 или
или 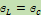
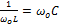 ⇒
⇒ 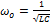
Особенности работы цепи с резонансом токов:
1) 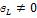 ;
; 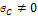 , но
, но 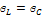 и
и 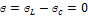
2) 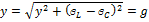 - min
- min
3) 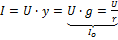 - min,
- min,
4) Т.к. 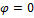 , то
, то 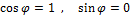 ;
; 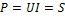 ;
; 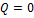
5) 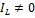 ;
; 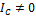 , но
, но 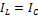 и
и 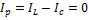
6) Весь ток протекает через активную проводимость: 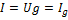
7) 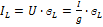 ⇒
⇒ 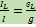 Если
Если 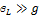 , то
, то 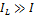
8) 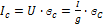 ⇒
⇒ 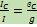 Eсли
Eсли 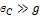 , то
, то 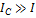
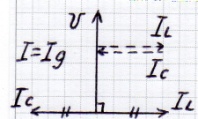
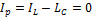
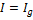
Добротность контура при резонансе токов.
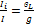 ;
; 
5.1.3. Резонанс в реальном параллельном колебательном контуре с потерями энергии.

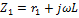
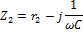
Найдем входную или эквивалентную проводимость тока:
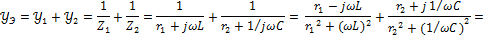
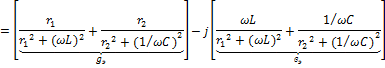
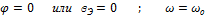
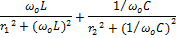
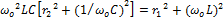
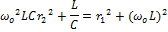


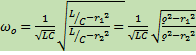 (1)
(1)
Проанализируем выражение (1)
Резонанс возможен только в том случае, если подкоренное выражение имеет положительный знак, т.е.:
1) 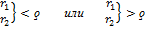 ;
;
2) 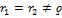 , то
, то 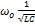 ;
;
3) 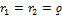 , то резонанс возможен на любой частоте (безразличный резонанс);
, то резонанс возможен на любой частоте (безразличный резонанс);
4) 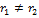 , но
, но 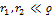
Тогда, 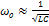
Частный случай: (в радиотехнике)
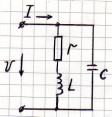
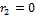
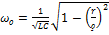 (2)
(2)
Следовательно, резонанс токов возможен только при условии: 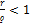
(3) 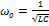 -
- 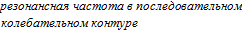
Сравнение уравнений (2) и (3) равно 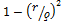
Если 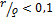 , то величины резонансных частот, рассчитанные по указанным формулам, отличаются не более, чем на 1%. Поэтому, добротность такого контура вычисляется по формуле:
, то величины резонансных частот, рассчитанные по указанным формулам, отличаются не более, чем на 1%. Поэтому, добротность такого контура вычисляется по формуле:
Дата: 2018-12-28, просмотров: 528.