3.2.1.Методы законов Кирхгофа (МЗК).
Метод не требует никаких преобразований схемы и пригоден для расчета любой цепи.
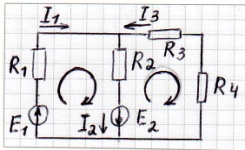
Дано: Е1, Е2; R1 ... R4
Определить токи в ветвях (МЗК)
Определяем число независимых уравнений, по законам Кирхгофа, которые по количеству равны числу ветвей или числу неизвестных токов.
Число уравнений по 1закону Кирхгофа (1зК) и 2 закону Кирхгофа (2зК) равно «в» – число ветвей.
По 1зК число уравнений равно числу узлов без единицы: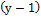 
.
По 2зК число уравнений равно числу ветвей: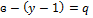 
– число независимых контуров.
Независимый контур – контур, в котором есть хотя бы одна ветвь, отсутствующая в других контурах
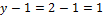
Сколько «стекол», столько независимых контуров !!!
Произвольно выбираем положительные направления токов в ветвях и направления обхода контуров:
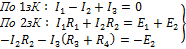1-ый контур
Решаем систему уравнений методом подстановки или методом определителей (метод Крамера):
∆ = 
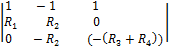≠ 0
I1 =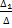 
; I2 = 
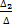; I3 = 
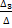, где
∆1 =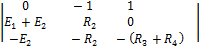 
и т.д.
3.2.2.Метод контурных токов.
Сначала, на основании уравнения 2зК, определяются контурные токи, которые замыкаются в независимых контурах. Это фиктивные токи. Затем, через контурные токи определяют токи в ветвях.
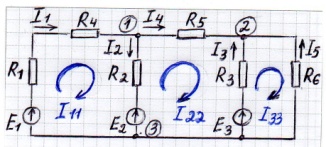
Дано: Е1, Е2, Е3 ; R1 ... R6
Определить токи в ветвях (МКТ)
ɞ = 5 ; у = 3 ; q = 3
1. Число уравнений по методу контурных токов (МКТ) равно q = 3.
2. Выбираем направление контурных токов в одну сторону.
3. Составляем систему уравнений:
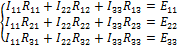, где
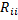– собственное сопротивление контура (сумма сопротивлений, входящих в контур, всегда с «+»);
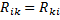- общее или взаимное сопротивление контуров 
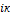(сумма сопротивлений, принадлежащих контуру 
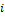и контуру к , всегда с «-»);
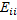– контурная ЭДС контура 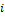(алгебраическая сумма ЭДС, входящая в контур).
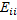+ , если совпадает с направлением контурного тока.
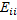- , если противоположно направлению контурного тока или направлению обхода.
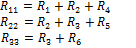
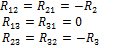
В общем виде для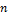 
независимых контуров система уравнений имеет вид:
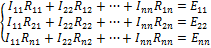
Контурное ЭДС:
; 
; 
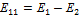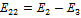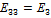
Решая систему уравнений методом определителей для контурного тока в К –контуре, получаем:
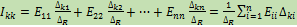(*) , где
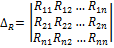≠ 0 (n – число независимых контуров);
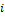- число независимых контуров.
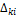- алгебраическое дополнение.
= 
= 
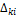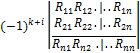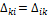
Далее определяются токи в ветвях через контурные токи. Для этого произвольно выбирают направление токов.
Токи в ветвях, которые принадлежат одному контору, равны контурному току с учетом выбранного направления. А токи в смежных ветвях равны разности контурных токов и совпадают по направлению с одним из них.
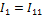
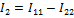
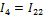
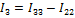
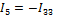
Примечание: если в схеме есть идеальный источник тока с внутренним сопротивлением, равным ∞, то ток этого источника надо выбрать в качестве контурного, при этом число неизвестных контурных токов и число уравнений сокращаются.
3.2.3.Метод наложения.
Метод применяется только для линейных цепей и формулируется:
ток К - ветви равен алгебраической сумме от каждой ЭДС - схемы в отдельности.
Выберем К - контур таким образом, чтобы К - ветвь входила только в этот контур, что всегда возможно. Тогда по формуле (*) (см.3.2.3):
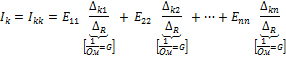
Каждую из контурных ЭДС можно выразить через ЭДС ветвей и сгруппировать в слагаемые при этих ЭДС:
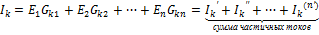
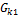... – только матем. смысл.
Суть метода:
1) рассчитываются частичные токи в ветви от каждого источника тока (ЭДС) в отдельности. При этом внутреннее сопротивление, отсутствующих источников в схеме, остается. Ветви с идеальными источниками ЭДС закорачиваются (Rвнутр=0), а ветви с идеальными источниками тока разрываются (Rвнутр=∞).
2) алгебраически суммируют частичные токи каждой ветви с учетом выбранных направлений.
Метод наложения целесообразно применять при числе источников не больше 3-х.
3.2.4.Метод узловых потенциалов. Метод 2-х узлов.
Сначала, на основании уравнения по 1зК, определяют потенциалы узлов, а затем через них рассчитывают токи в ветвях.
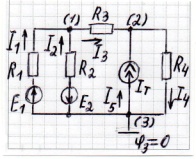
Дано: Е1, Е2,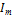 
R1 ... R4
Определить токи в ветвях (МУП)
1. Число уравнений по МУП равно (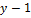 
)= 2 (ур.)
2. Потенциал одного из узлов принимается за 0:
𝜑3 = 0 – базисный узел.
3. Система уравнений: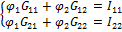 
, где
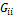– собственная проводимость узла 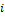(сумма проводимостей ветвей, сходящихся в узле ).
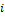Всегда берется со знаком «+».
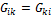
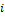общая проводимость и К (сумма проводимостей ветвей между 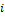и К, всегда со знаком « »).
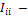узловой ток узла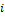 алгебраическая сумма токов от источников ЭДС и от источников тока,
сходящихся в узле .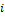
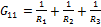
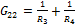
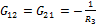
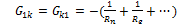
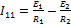
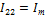
В общем виде для n узлов система содержит (n – 1) уравнений:
(**)
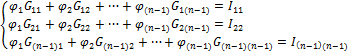
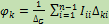∆6 – определитель системы, элементы которой являются проводимостями: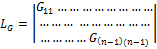 
≠ 0
= 
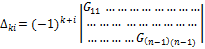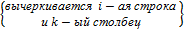
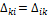
Найдя потенциалы узлов, находим токи в ветвях, определяя произвольно их направления:
; 
; 
; 
; 
= .
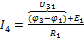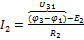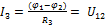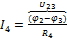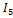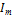Примечание: при наличии ветвей с идеальным источником ЭДС (RВНУТ=0) целесообразно принять за базисный узел один из узлов, к которому присоединена данная ветвь. Тогда, потенциал 2-го узла становится известным и число уравнений сокращается.
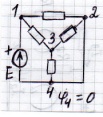
у = 4
у 1 = 3
𝜑4 = 0 ⇒ 𝜑1 = Е
Метод 2-х узлов:
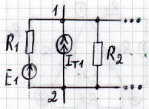
𝜑2 = 0 ;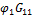 
+ 
= 
; 
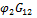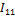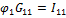
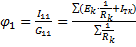
Правило знаков: по 1 закону Кирхгофа.
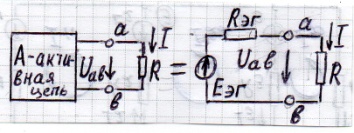
3.2.5. Метод эквивалентного генератора.
Используется для расчета тока в одной ветви сложной электрической цепи. Метод основан на теореме Тевенена.
Теорема Тевенена: ток в любой ветви 
линейной электрической цепи не изменится, если электрическую цепь, к которой подсоединена данная ветвь, заменить эквивалентным генератором.
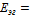
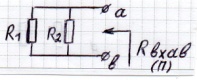
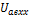- равна напряжению на зажимах разомкнутой цепи 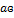(режим холостого хода).
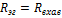- равно сопротивлению пассивной электрической цепи между точкам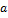и 
и 
при отключенной
ветви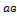 
.
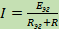
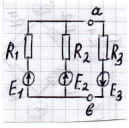Примеры теоремы:
Дано: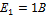 
; 
; 
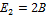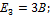
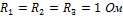
Определить: 
- ? (МЭГ)
1) Определяем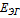 
: 
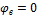
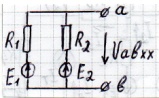
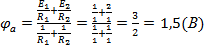
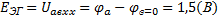
2) Определяем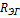 
:
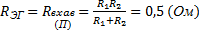
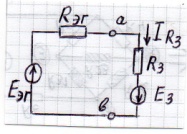
3) Ищем ток :
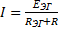
Дата: 2018-12-28, просмотров: 390.
