1. Проблема демаркации онтологического и гносеологических аспектов математического знания.

2. Краткий экскурс в историю математики.

3. Проблема обоснования математического знания.

 источник. Философия науки. "Постнеклассические проблемы философии науки". Глава 1. 2015. Нижний Новгород.

+ список литературы.

 "Антология философии и науке". Барабашов 2002

Рузавин Г.И. "Философские проблемы математики".

Рыбников. "История математики"

 Проблема демаркации онтологического гносеологического знания.

Античные ученые считали математику частью реальности, шифры существуют сами по себе в реальности.

Проблема демаркации. Попытка разделить объективную и субъективную часть.

НО

Платон считал, что слушать в вещах нет. Вещественный мир не содержит численных величин. Полагал что люди в дар от мирового разума получают способность понимать и мыслить цифрами. Для Платона в начале - идея. Математическое знание не получают методом наблюдения. Оно не образуется из непосредственного контакта с материальным миром, математическое знание врождённое.

Человек причастен к созданию математического знаний, но что-то от него не зависит. Это различение (одно от другого) и есть проблема.

Математический атомизм. Геометрия , геометрические фигуры, существованием обязаны природе атома.

 Для Аристотеля математика - наука о знании, о потоках атомов. Геометрия - наука о природных явлениях. Математическое знание формулируется человеком, который списывает с природы образцы, дополняя своими пониманиями. Но, например, человек не в силах изобразить предел, поэтому он схематизирует, интерпретирует что-то по-своему. Математика не врождена.

 Ньютон полагал, что математические величины, соотношения есть формы механического движения. Исследователи выявляют математическую составляющую в мире.

Согласен с Галилеем в том смысле, что исследователь не может мыслить не математически, так как природа структурированное математически.

По Галилео природа написана на языке математики.

Лейбниц считал, что математическое знание не имеет вещественной природы, создается человеком, являет исключительно духовное основание. Математическое знание не свойство природы.

Коши доказал теорему существования: математика не имеет эмпирического основания. Математическое исследование не имеет эмпирического уровня.

Выражает ли математический уровень объективных знаний, объективных процессов, существующих вне мыслей, или отражает содержание самой мысли?

Математика имеет теоретическую природу. Она хорошо применима для количественного описания процессов. Но природа математики не ясна.

Развитость науки определяется степенью применения в ней математики.

Математика позволяет теоретически сформулировать знания по мире.

До неолитической революции (переход от собирательства, рыболовства, охоты к производству и земледелию, ремёслам) математика не носила научного основания.

В античности уже широко применялась математика. Наука родилась в Древней Греции (там возникла доказательство).

Математика выражает содержание мысли о количественных пропорциях, соотношениях. Всякое математическое знание имеют знаковую форму, абстрактно, не имеет качественный основы. Этим очень близко к философскому. Обладает идеализацией. Математика приводит какой-либо признак до крайности реального существования.

 Логический характер математического знания.

 Предмет математического знания есть количественные изменения. Объектом математического исследования является преднамеренно выстроенные идеализированные структуры. Объект есть аналог реальных количественных изменений.

Математика развиваются, выявляет все новые аспекты . Какое всё-таки истинно? Каков критерий математического знания?

 Проблема обоснования математического знания.

По Коши: то математическое знание верно, которое не имеет внутреннего противоречия.

Требование непротиворечивости остается декларацией до тех пор, пока не изобретен способ обоснования непротиворечивости.

Не работая со свойствами вещей и процессов, математика дает им описание.

Кантер. Теория множеств. Для чего угодно есть теория множеств.

Рассел. Математическая лингвистика. Логический подход. Все математические концепции имеют своим стержнем логику. Не могут существовать множества, включающие себя и не включающие себя.

Интуитивистский подход. Рейель. Математика существует в спонтанном движение мысли. Новые изменения могут фиксироваться неподконтрольно.

Марков. Теория структур. Метод математической гипотезы и математического

В основе математических теорий лежит аксиоматический метод.

 Математическое знание до науки существовала в виде счёта реальных физических объектов.

Как наука математика началась с адекватности теорий с выведением доказательства.

Проблемы сопоставления количества одного качества и количества другого качества есть проблема счета. Сколько нужно глиняных горшков, чтобы получить корову?

Первое доказательство – уравнение: одну часть сводим к другой.

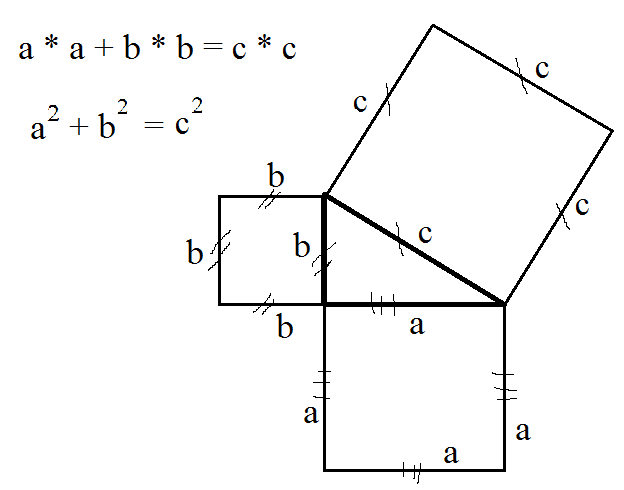
Символика появилась до науки.

Число объективно, но есть отражение количества в мыслях человека. Числа существуют независимо от человека (по Пифагору).

Математическое знание абстрагируется от качественной стороны реальных вещей, берёт только количественные.

Математическое знание не есть знание только о природе, а обо всём.

В XIX - XX веках математика не считалось наукой в естествознании. Она стала наукой о количественной стороне изменений в самых разных науках.

Формализация. Мысли о количественных изменениях выражается в законах, формула, зависимостях.

В любой науке эмпирическое исследование завершается формулированием суждения на основе данных (опыт, протокольные суждения).

Математическое знание усваиваются на основании культурных достижений прошлых поколений (искусственный продукт деятельности).

Джон Локк говорил:" врождённого математического знания нет".

Гносеологическая природа математического знания не тождественна психологической.

Минимум затрат при максимуме качества.

Максимизация вычислений позволяет получить результат, который непосредственно от нас не зависит. Она (программа) работает на основании заложенных циклов, методик, моделируя ход мысли. Полученный результат дает почву для размышления. Но это не дает эмпирического уровня, машина не приходит в контакт с эмпирической установкой.

С помощью вычислительных устройств можно оцифровать эксперимент (измерительную установку) и осуществить переход эмпирического к теоретическому уровню исследования (автоматизация исследования).