План

1. Свойство рефлексивености

2. Свойство симметричности

3. Свойство транзитивности

Свойства отношений

Мы установили, что бинарное отношение на множестве X пред­ставляет собой множество упорядоченных пар элементов, принад­лежащих декартову произведению X х Х. Это математическая сущ­ность всякого отношения. Но, как и любые другие понятия, отноше­ния обладают свойствами. Их удалось выделить, изучая различные конкретные отношения. Свойств достаточно много, в нашем курсе мы будем изучать только некоторые.

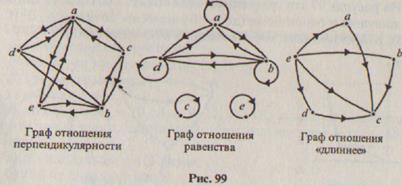
Рассмотрим на множестве отрезков, представ­ленных на рис. 98, отношения перпендикулярно­сти, равенства и «длиннее». Построим графы этих отношений (рис. 99) и будем их сравнивать. Ви­дим, что граф отношения равенства отличается от двух других наличием петель в каждой его вершине. Эти петли - результат того, что отно­шение равенства отрезков обладает свойством: любой отрезок равен самому себе. Говорят, что отношение равенства обладает свойством рефлек­сивности или просто, что оно рефлексивно.

Определение. Отношение R на множестве X называется рефлексив­ным, если о каждом элементе множества X можно сказать, что он находится в отношении R с самим собой.

Используя символы, это отношение можно записать в таком виде:

R рефлексивно на Х ↔ х R х для любого х ? X.

^опр.

Если отношение R рефлексивно на множестве X, то в каждой вер­шине графа данного отношения имеется петля. Справедливо и обрат­ное утверждение: граф, каждая вершина которого имеет петлю, задает отношения, обладающие свойством рефлексивности.

Примеры рефлексивных отношений:

- отношение «кратно» на множестве натуральных чисел (каждое натуральное число кратно самому себе);

- отношение подобия треугольников (каждый треугольник подо­бен самому себе).

Существуют отношения, которые свойством рефлексивности не обладают. Таким, например, является отношение перпендикулярности на множестве отрезков: нет ни одного отрезка, о котором можно ска­зать, что он перпендикулярен самому себе. Поэтому на графе отноше­ния перпендикулярности (рис. 99) нет ни одной петли. Не обладает свойством рефлексивности и отношение «длиннее» для отрезков.

Обратим теперь внимание на графы отношений перпендикулярно­сти и равенства отрезков. Они «похожи» тем, что если есть одна стрелка, соединяющая пару элементов, то обязательно есть и другая, соединяющая те же элементы, но идущая в противоположном направ­лении. Эта особенность графа отражает те свойства, которыми обла­дают отношения параллельности и равенства отрезков:

- если один отрезок перпендикулярен другому отрезку, то этот «другой» перпендикулярен первому;

- если один отрезок равен другому отрезку, то этот «другой» равен первому.

Про отношения перпендикулярности и равенства отрезков гово­рят, что они обладают свойством симметричности или просто сим­метричны.

Определение. Отношение R на множестве X называется симмет­ричным, если выполняется условие: из того, что элемент х находит­ся в отношении R с элементом у, следует, что и элементу находит­ся в отношении R с элементом х.

Используя символы, это отношение можно записать в таком виде:

R симметрично на Х ↔ (х R y → yRx).

                                                                        ^опр.

Граф симметричного отношения обладает особенностью: вместе с каждой стрелкой, идущей от х к у, граф содержит и стрелку, идущую от у к x. Справедливо и обратное утверждение. Граф, содержащий вместе с каждой стрелкой, идущей от x к у, и стрелку, идущую от у к x, является графом симметричного отношения.

В дополнение к рассмотренным двум примерам симметричных от­ношений присоединим еще такие:

-отношение параллельности на множестве прямых (если прямая x параллельна прямой у, то и прямая у параллельна прямой х)

-отношение подобия треугольников (если треугольник F подобен треугольнику Р, то треугольник Р подобен треугольнику F).

Существуют отношения, которые свойством симметричности не обладают. Таким, например, является отношение «длиннее» на мно­жестве отрезков. Действительно, если отрезок x длиннее отрезка у, то отрезок у не может быть длиннее отрезка х. Про отношения «длиннее» говорят, что оно обладает свойством антисимметрично­сти или просто антисимметрично.

Определение. Отношение R на множестве X называется анти­симметричным, если для различных элементов х и у из множества X выполнено условие: из того, что х находится в отношении R с элементом у, следует, что элемент у в отношении R с элементом х не находится.

Используя символы, это определение можно записать в таком виде:

R симметрично на Х ↔ (х R y _^ x≠ y → yRx).

                                                                  ^опр.

Граф антисимметричного отношения обладает особенностью: если две вершины графа соединены стрелкой, то эта стрелка только одна. Справедливо и обратное утверждение: граф, вершины которого со­единены только одной стрелкой, есть граф антисимметричного отношения.

Кроме отношения «длиннее» на множестве отрезков свойством ан­тисимметричности, например, обладают:

- отношение «больше» для чисел (если х больше у, то у не может
быть больше х);

- отношение «больше на 2» для чисел (если х боль­ше у на 2, то у не может быть больше на 2 числа х),

Существуют отношения, не обладающие ни свой­ством симметричности, ни свойством антисиммет­ричности. Рассмотрим, например, отношение «быть сестрой» на множестве детей одной семьи. Пусть в семье трое детей: Катя, Маша и Толя. Тогда граф отношения «быть сестрой» будет таким, как на рисунке 100. Он показывает, что данное отношение не обладает ни свой­ством симметричности, ни свойством антисимметричности.

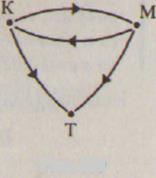
Рис.100

Обратим внимание еще раз на одну особенность графа отноше­ния «длиннее» (рис. 99). На нем можно заметить: если стрелки про­ведены от е к а и от а к с, то есть стрелка от е к с; если стрелки приведены от е к b и от b к с, то есть стрелка и от е к с и т.д. Эта особенность графа отражает важное свойство отношения «длиннее»: если первый отрезок длиннее второго, а второй - длиннее третьего, то первый - длиннее третьего. Говорят, что это отношение обладает свойством транзитивности или просто транзитивно.

Определение. Отношение R на множестве X называется транзи­тивным, если выполняется условие; из того, что элемент х нахо­дится в отношении R с элементом у и элемент у находится в от­ношении R с элементом z, следует, что элемент х находится в от­ношении К с элементом z .

Используя символы, это определение можно записать в таком виде:

R транзитивно на X ↔ (х R y _^ yRz → xRz).

                                                                  ^опр.

Граф транзитивного отношения с каждой парой стрелок, идущих от x к у и у к z, содержит стрелку, идущую от х к z. Справедливо и обратное утверждение.

Кроме отношения «длиннее» на множестве отрезков свойством транзитивности обладает отношение равенства: если отрезок х равен отрезку у и отрезок у равен отрезку z, то отрезок х равен отрезку z, Это свойство отражено и на графе отношения равенства (рис. 99)

Существуют отношения, которые свойством транзитивности не об­ладают. Таким отношением является, например, отношение перпенди­кулярности: если отрезок а перпендикулярен отрезку d, а отрезок d перпендикулярен отрезку b, то отрезки а и b не перпендикулярны!

Рассмотрим еще одно свойство отношений, которое называют свой­ством связанности, а отношение, обладающее им, называют связанным.

Определение. Отношение R на множестве X называется связан­ным, если для любых элементов х и у из множества X выполняется условие: из того, что х и у различны, следует, что либо х находит­ся в отношении R с элементом у, либо элемент у находится в от­ношении R с элементом х.

Используя символы, это определение можно записать в таком виде:

R связано на множестве X  ↔ (х ≠ у => х Rу v у Rх).

^опр.

Например, свойством связанности обладают отношения «больше» для натуральных чисел: для любых различных чисел х и у можно ут­верждать, что либо х > у, либо у > х.

На графе связанного отношения любые две вершины соединены стрелкой. Справедливо и обратное утверждение.

Существуют отношения, которые свойством связанности не обла­дают. Таким отношением, например, является отношение делимости на множестве натуральных чисел: можно назвать такие числа х и у, что ни число х не является делителем числа у, ни число у не является делителем числа х.

Выделенные свойства позволяют анализировать различные отно­шения с общих позиций - наличия (или отсутствия) у них тех или иных свойств.

Так, если суммировать все сказанное об отношении равенства, за­данном на множестве отрезков (рис. 99), то получается, что оно реф­лексивно, симметрично и транзитивно. Отношение «длиннее» на том же множестве отрезков антисимметрично и транзитивно, а отношение перпендикулярности - симметрично, но оно не обладает свойствами рефлексивности и транзитивности. Все эти отношения на заданном множестве отрезков связанными не являются.

Задача 1. Сформулировать свойства отноше­ния R, заданного при помощи графа (рис. 101).

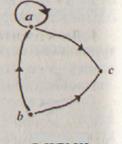
Рис.101

Решение. Отношение R-антисимметрично, так как вершины графа соединяются только одной стрелкой.

Отношение R - транзитивно, так как с парой стрелок, идущих от b к а и от а к с, на графе есть стрелка, идущая от b к с.

Отношение R - связанно, так как любые две вер­шины соединены стрелкой.          

Отношение R свойством рефлексивности не обла­дает, так как на графе есть вершины, в которых петли нет.

Задача 2. Сформулировать свойства отношения «больше в 2 раза», заданного на множестве натуральных чисел.

Решение. «Больше в 2 раза» - это краткая форма отношения «число х больше числа у в 2 раза». Это отношение антисимметрично, так как выполняется условие: из того, что число х больше числа у в 2 раза, следует, что число y не больше числа x 2 раза.

Данное отношение не обладает свойством рефлексивности, пото­му что ни про одно число нельзя сказать, что оно больше самого себя в 2 раза.

Заданное отношение не транзитивно, так как из того, что число x больше числа у на 2, а число у больше числа z на 2, следует, что число х не может быть больше числа z на 2.

Это отношение на множестве натуральных чисел свойством связан­ности не обладает, так как существуют пары таких чисел х и у, что ни число х не больше числа у в два раза, ни число у не больше х в 2 раза. Например, это числа 7 и 3, 5 и 8 и др.

Упражнения

1. Докажите, что отношение R, заданное при помощи графа (рис.102), рефлексивно, анти­симметрично и транзитивно.

2. Докажите, что отношение Т, заданное при помощи графа (рис.103), симметрично и тран­зитивно.

3. Сформулируйте условия, при которых от­ношение свойством рефлексивности не облада­ет, и докажите, что отношение Т (см. упр. 2) не рефлексивно.

4. Сформулируйте условия, при которых от­ношение не обладает свойством: а) симметричности; б) антисимметричности; в)транзитивно­сти; г) связанности.

5. Докажите, что отношение Р, граф которого изображен на рисунке 104, не обладает ни свойством симметричности, ни свойством антисимметричности, ни свойством транзитив­ности.

6. Какими свойствами обладает отношение, граф которого изображен на рисунке 105? Яв­ляется ли оно рефлексивным? Транзитивным?

7. Какие из следующих утверждений истинны:

а) Отношение «x больше у на 3» антисимметрично на множестве N, так как из того, что х больше у на 3, не следует, что у больше х на 3.

б) Отношение «x больше у на 3» антисимметрично, так как из того, что х больше у на 3, следует, что у не больше х на 3.

в) Отношение «х больше у на 3» антисим­метрично, так как из того, что х больше у на 3, следует, что у меньше х на 3.

8. На множестве отрезков задано отношение «короче». Верно ли, что оно антисимметрично
и транзитивно? Рефлексивно ли оно?

9. Какими свойствами обладают следующие отношения, заданные на множестве натуральных чисел:

а) «меньше»; б) «меньше на 2»; в) «меньше в 2 раза»?

10. На множестве X ={а, b, с} задано отношение R = {(а, b), (а, а), ( b, b), (с, с), ( b, а), ( b, с), (с, b)}. Какими свойствами оно обладает?

11. На множестве Х= {2,4,6,8, 12} заданы отношения «больше» и «кратно». В чём их сходство и различие?

12. Установите, какое отношение рассматривается в задаче; какие приемы анализа задачи можно использовать:

а) Школьники сделали к карнавалу 15 шапочек для мальчиков, а для девочек в 2 раза больше. Сколько всего карнавальных шапочек они сделали?

б) Второклассники вырезали для елки 26 звездочек, это в 2 раза меньше, чем снежинок. Сколько всего звездочек и снежинок вырезали второклассники?