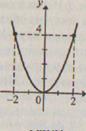Числовые функции можно представлять наглядно на координатной плоскости. Пусть у = f(х) - функция с областью определения X. Тогда ее графиком является множество таких точек координатной плоскости, которые имеют абсциссу х и ординату f(х) для всех х из множества X.
Так, графиком функции у = 2х - 3, заданной на множестве R, является прямая (рис. 82), а графиком функции у = х2, заданной также на множестве R - парабола (рис. 83).
|
|
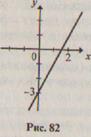
Рис. 83
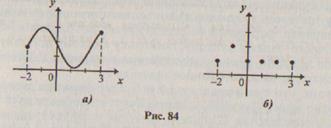
Функции можно задавать при помощи графика. Например, графики, приведенные на рисунке 84, задают функции, одна из которых имеет в качестве области определения промежуток [-2, 3], а вторая конечное множество {-2, -1,0, 1,2,3}.
 Не каждое множество точек на координатной плоскости представляет собой график некоторой функции. Так как при каждом значении аргумента из области определения функция должна иметь лишь одно значение, то любая прямая, параллельная оси ординат, или совсем не пересекает график функции, или пересекает его лишь в одной точке. Если же это условие не выполняется, то множество точек координатной плоскости график функции не задает. Например, кривая на рисунке 85 не является графиком функции - прямая АВ, параллельная оси ординат, пересекает ее в двух точках.
Не каждое множество точек на координатной плоскости представляет собой график некоторой функции. Так как при каждом значении аргумента из области определения функция должна иметь лишь одно значение, то любая прямая, параллельная оси ординат, или совсем не пересекает график функции, или пересекает его лишь в одной точке. Если же это условие не выполняется, то множество точек координатной плоскости график функции не задает. Например, кривая на рисунке 85 не является графиком функции - прямая АВ, параллельная оси ординат, пересекает ее в двух точках.
Функции можно задавать при помощи таблицы. Например, таблица, приведенная ниже, описывает зависимость температуры воздуха от времени суток. Эта зависимость - функция, так как каждому значению времени t соответствует единственное значение температуры воздуха р:
| t (в часах) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| p( в градусах Цельсия) | -3 | -7 | -5 | 0 | 2 | 4 | 2 | 1 | -3 |
Числовые функции обладают многими свойствами. Мы рассмотрим одно из них - свойство монотонности, так как понимание этого свойства учителем важно при обучении математике младших школьников.
Определение. Функция f(х) называется монотонной на некотором промежутке А, если она на этом промежутке возрастает или убывает.
Определение. Функция f(х) называется возрастающей на некотором промежутке А, если для любых чисел х1, х2 из множества А выполняется условие:
х1< х2 ð f(х1)< f(х2)
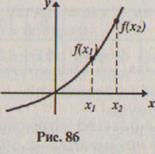
График функции, возрастающей на промежутке А, обладает особенностью: при движении вдоль оси абсцисс слева направо по промежутку А ординаты точек графика увеличиваются (рис. 86).
Определение. Функция f называется убывающей на некотором промежутке А, если для любых чисел х1, х2 из множества А выполняется условие:
х1< х2 ð f(х1)> f(х2)
График функции, убывающей на промежутке А, обладает особенностью: при движении вдоль оси абсцисс слева направо по промежутку А ординаты точек графика уменьшаются (рис. 87).

Упражнения
1. Функции, приведенные в начале пункта, задайте при помощи формул и укажите для каждой область определения и множество значений.
2. Какие из следующих формул задают на множестве R действительных чисел функцию:
а) у = 4х; б) y = 4/x; в) x2 + у2 = 4?
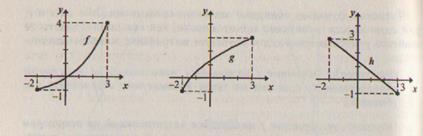
Рис.88
3. На рисунке 88 изображены графики функций f, g, h . Укажите область определения и область значений каждой. Установите, возрастают они или убывают на данной области определения. Найдите для каждой функции наибольшее и наименьшее значение на всей области определения.
4. Постройте график функции у = 5 - х, если ее область определения X такова:
а) X = {0,1,2,3,4,5};
б) X =[0;5];
в) X = R.
5. Постройте графики следующих функций при условии, что они заданы на множестве R действительных чисел:
а) y = х; 6) y= 3; в) х = 5; г) y = 0.
6. Функция f задана при помощи таблицы:
| X | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| у | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
а) Укажите ее область определения и область значений.
б) Задайте функцию f при помощи формулы.
в) Постройте график функции f на координатной плоскости.
д) Докажите, что функция f возрастает на всей области определения.
7. Изучая математику в начальных классах, учащиеся выполняют задания:
а) 39 + a. Вычисли сумму, если а принимает значения 0,6,15,31,46,52.
б)¨ -9. Вычисли разность, поставив в окошко числа 10, 11,12.
в) Составь все возможные примеры на сложение однозначных чисел с ответом 12.
Покажите, что в каждом из этих заданий устанавливается соответствие между двумя числовыми множествами и это соответствие - функция. Назовите в каждом случае область ее определения и область значений.
8. Докажите, что соответствие между значениями переменных х и у, осматриваемое в задаче, является функцией; укажите область ее значений при условии, что х < 5; постройте график данной функции:
а) Катя купила 3 тетради, а Лена на х тетрадей больше. Сколько тетрадей (у) купили Лена и Катя вместе?
б) Из пунктов А и В навстречу друг другу вышли два туриста. При встрече оказалось, что один прошел 3 км, а второй на х км больше. Каково расстояние (у км) между пунктами А и В?
9. Сравните функции, о которых идет речь в упражнении 8. Чем они похожи? В чем их различие? Какими будут графики данных функций?
10. У одного ученика было 2 тетради. В течение 6 дней он каждый день покупал по 3 новых тетради. Сколько тетрадей (у) у него будет через х дней?
Выразите у через х и покажите, что установленное соответствие - функция. Укажите ее область определения и область значений. Постройте график.
Лекция 19. Прямая и обратная пропорциональность
План:
1. Прямая и обратная пропорциональность, линейная и квадратичная функции, их свойства и графики.
2. Построение графиков функций.
3. Основные выводы
Дата: 2019-02-02, просмотров: 501.