В условиях современного поточного производства центрифуги периодического действия вытесняются центробежными машинами с непрерывным отводом осадка (центрифугами непрерывного действия). Центрифуги с такой особенностью производственного цикла, помимо непрерывности процесса отвода продуктов центрифугирования, отличаются от центрифуг периодического действия сравнительной простотой конструкции и низким удельным энергопотреблением.
В настоящее время известны такие промышленные конструкции центробежных машин непрерывного действия как: вибрационные центрифуги, многокаскадные центрифуги с пульсирующей выгрузкой, высокоскоростные со шнековой выгрузкой, ступенчатые со шнековой выгрузкой, комбинированные осадительно-фильтрующие центрифуги и др.
Показанная на рис. 7.1, 7.2 схема относится к рабочему объему (барабану) так называемой трубчатой центрифуги.
| z |
| w |
| L |
| r0 |
| R |
| О |
| Суспензия |
| Ротор |
Рис. 7.1
| r0 |
| R |
| L |
| r |
| O |
| vz |
| vr |
| Осадок |
| Фугат |
| Суспензия |
| z |
| w |
| частица |
| А |
| В |
| С(R,z) |
Рис. 7.2.
Интегральные показатели взвеси, седиментирующего в роторе центрифуги непрерывного действия
Если требуется организовать процесс седиментации взвеси в жидкости в условиях непрерывного технологического потока, то для реализации этой цели и для интенсифиции данного процесса целесообразно использовать именно центрифугу непрерывного действия. При этом естественным аналогом процесса осаждения частиц в роторе центрифуги непрерывного действия, как и в роторе центрифуги периодического действия, следует считать процесс седиментации взвеси в условиях свободного отстоя. Причем, по-прежнему, считают, что кинетики процесса седиментации частиц в поле силы тяжести и в центробежном силовом поле различаются лишь интенсивностью силового воздействия на обрабатываемую жидкостную смесь. Что обусловливает постановку и количественный анализ разделения суспензии в роторе центрифуги непрерывного действия.
В дальнейшем, как и при анализе процесса седиментации частиц в роторе центрифуге периодического действия, в предположении, обрабатываемая суспензия представляет собой малоконцентрированную жидкостную смесь, считают, что ротор центрифуги с непрерывным отводом осадка приведен во внезапное вращательное движение с угловой скоростью w, а ограниченный областью r0 £ r £ R (где r0 и R, соответственно, радиус свободной поверхности жидкости и радиус ротора), 0 £ z £ L (где L - длина ротора) поток движется в положительном направлении оси z в поршневом режиме (рис. 7.1), т.е. с постоянной расходной скоростью и поэтому
ur = 0, uz = u0, (7.1)
где u = { ur, uz}- вектор скорости потока жидкости; ur, uz - соответственно, радиальная и осевая составляющие скорости u,
u0 = 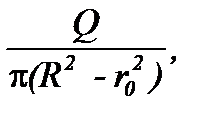 (7.2)
(7.2)
где Q - производительность (расход) центрифуги по жидкости.
При этом показано, что интродуцированная в данный поток частица небольшого размера в относительном движении перемещается практически по радиусу, с небольшой скоростью.
С целью исследовать кинетику частицы, формально, силу тяжести G заменяют центробежной силой
Fцб = Vrтw2r,
где V и rт - соответственно, объем и плотность частицы, r - радиальная координата (рис. 7.2), и, в таком случае, на основе принципа Даламбера записывают
Fцб + FАр + Fc = 0, (7.3)
или, принимая для определенности rт > rж, в проекциях (7.3) на радиальное направление:
VDrw2r + Fcr = 0, (7.4)
на осевое направление:
Fcz = 0, (7.5)
где Dr = rт - rж.
Если классифицируемая по размеру взвесь состоит из высокодисперсных частиц, то силу сопротивления Fc рассчитывают по формуле Стокса
Fc = -3pmd(v - u), (7.6)
где v = { vr,vz}- вектор скорости частиц; vr,vz - соответственно, радиальная и осевая составляющие скорости v; m - динамическая вязкость жидкости, d - диаметр частицы.
Тогда, подставляя (7.6) в (7.3), c учетом (7.4), (7.5) получают, в проекциях по осям r, z
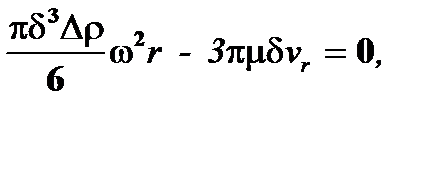
vz - uz = 0,
откуда имеют
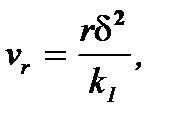 vz = uz = u0, (7.7)
vz = uz = u0, (7.7)
где обозначено
k1 = 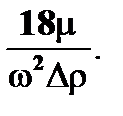 (7.8)
(7.8)
Таким образом, на основе (7.7) приходят к выводу о том, что в радиальном направлении частица движется ускоренно по радиусу, а в осевом направлении перемещается одинаково с потоком жидкости, т.е. как взвешенная.
Согласно кинематическим зависимостям по проекциям скорости частицы
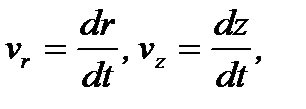
и поэтому,
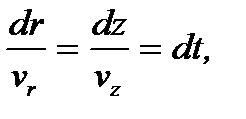
в результате приходят к дифференциальному уравнению движения частицы в плоскости rz
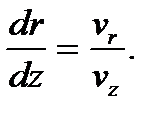 (7.9)
(7.9)
Подставляя (7.7) в (7.9) и разделяя, затем, переменные получают
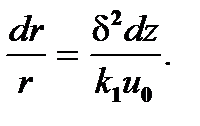 (7.10)
(7.10)
Интегрируя (7.10) по траектории частицы А(r, 0) до B(0, L) (рис. 7.2), т.е., слева по r в пределах от r до R, справа по z от 0 до L, находят частное решение уравнения (7.10)
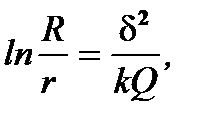
где, согласно (7.2), (7.8), обозначено
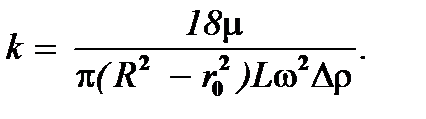 (7.11)
(7.11)
откуда получают выражение текущего критического диаметра частицы, движущейся по траектории АВ, как функции координаты r
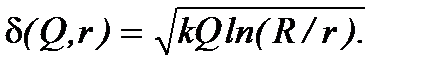 (7.12)
(7.12)
Физический смысл определяемой по (7.12) величины, как обычно, состоит в том, что любые гипотетические частицы диаметром d¢ > d, исходящие из точки А(r, 0), достигнут стенку ротора (и осядут на ней) в точке С(R, z), такой, что z < L (рис. 7.2).
С целью получить наибольшее из значений dк критического диаметра частицы в формуле (7.11) полагают r = r0, в результате имеют
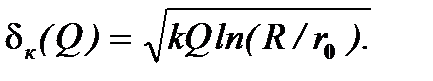 (7.13)
(7.13)
В свою очередь, из формулы (7.13) следует зависимость производительности Q центрифуги от значения dк
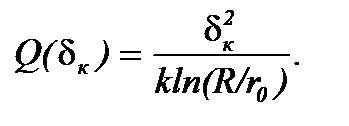 (7.14)
(7.14)
Для того чтобы получить интегральную характеристику по количеству оседающих в единицу времени на стенке ротора частиц, из цилиндрического объема r0 £ r £ R и высотой w0, выделяю элементарную трубку радиусами r, r + dr и той же высоты (рис. 7.2).
Причем, из выделенного объема суспензии в единицу времени осаждается количество частиц, равное
dn1 = (2prdr)w0n0Ф[d(r,t)], (7.15)
где Ф(d) = 1 - F(d), F(d),Ф(d) - соответственно, счетная и характеристическая функции распределения частиц по крупности в исходной суспензии.
Интегрируя (7.15) слева по числу n оседающих частиц, а справа - по r - по толщине потока, имеют
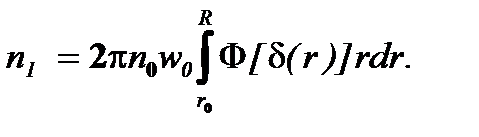 (7.16)
(7.16)
С другой стороны, так как тот же объем суспензии включает p(R2 - r02)w0n0 частиц, то в качестве счетного коэффициента осветления, в силу (7.16), принимают
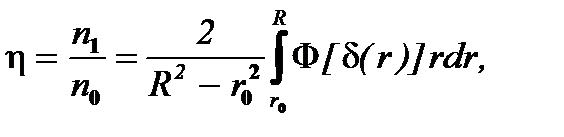 (7.17)
(7.17)
а в качестве счетного коэффициента уноса
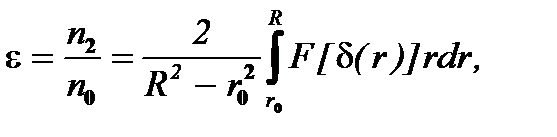 (7.18)
(7.18)
где n1(Q), n2(Q) - соответственно, количество частиц, сохранившихся в суспензии в единицу времени в единице объема в осветленной суспензии (фугате) и количество частиц, осадившихся в единицу времени из суспензии на стенке ротора (r = R, 0 < z < L), в том же объеме, d(r) рассчитывается по (7.12) .
Принимая во внимание формулы (7.12), например, для коэффициента уноса e (7.18) получают в явной форме
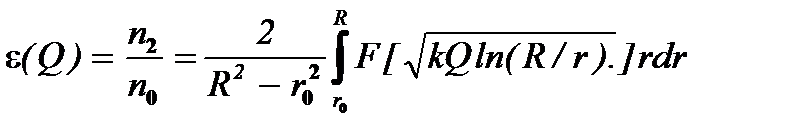 (7.19)
(7.19)
или, c учетом формулы (7.13)
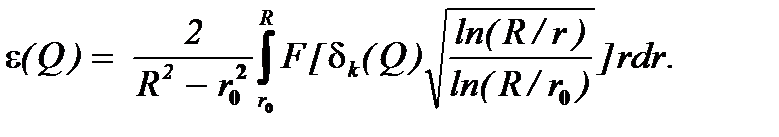 (7.20)
(7.20)
Переписывая (7.20) в явной форме, имеют
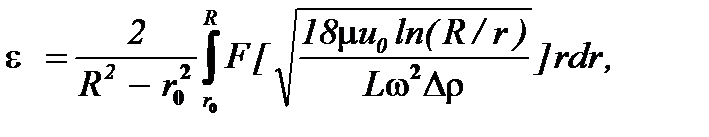 (7.21)
(7.21)
откуда, учитывая, что F(0) = 0, F(¥) = 1, и переходя к пределам по физико-механическим и геометрическим параметрам процесса получают
limm ®0e = 0, limu0®0e = 0, limu0®¥e = 1,
limw®¥e = 0, limL®¥e = 0, lim Dr®0e = 1,
что соответствует физическому смыслу коэффициенту e уноса.
Выражая u0 в соответствии с (7.2), придают коэффициенту (7.19) вид
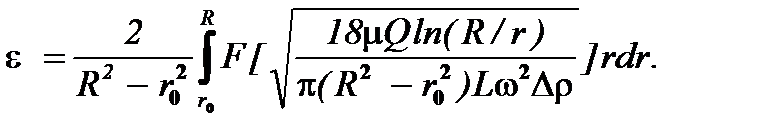 (7.22)
(7.22)
Как видно по структуре формулы (7.22), подкоренное выражение в аргументе функции F, зависит от всех основных параметров процесса разделения суспензии в роторе центрифуги непрерывного действия. При этом в реальных условиях в качестве управляющего параметра процесса классификации частиц проще всего выбирать либо угловую скорость w, либо производительность Q центрифуги.
В дальнейшем управляющим параметром процесса выбирают производительность Q .
Поскольку F¢(d) > 0, R > r, то в соответствии с (7.22) частная производная по Q коэффициента уноса
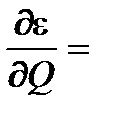
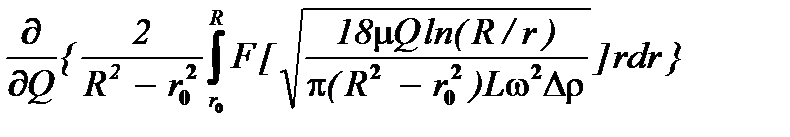 =
=
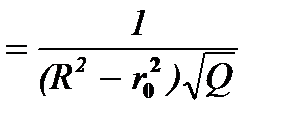
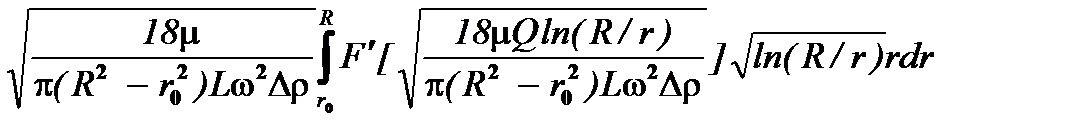 > 0.
> 0.
Откуда вытекает, что, как и должно быть, коэффициент уноса e(Q) возрастает вместе с производительностью центрифуги по закону Q-1/2, т.е. сравнительно медленно (т.е. острота разделения снижается одновременно при увеличении производительности машины).
Соответственно, при тех же условиях, коэффициент осветления h является возрастающей функцией по Q .
Аналогично, на основе (7.20) можно показать, что
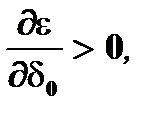
и поэтому, коэффициент уноса возрастает, а коэффициент осветления
убывает (условия осветления ухудшаются).
В дальнейшем, формулы (7.20) - (7.22) полагают в основу количественного анализа процесса разделения высокодисперсных частиц в роторе центрифуги непрерывного действия.
Дата: 2019-02-02, просмотров: 374.