Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Дифференциальные уравнения движения вязкой несжимаемой жидкости (уравнения Навье-Стокса).

При выводе этих уравнений принимают допущения о том, что жид­кость несжимаема и не поддается растяжению. Если  в потоке вязкой жидкости выделить  элементарный параллелепипед (рис. 4.1), то дей­ствие на него силы трения, обусловленной вязкостью потока, прояв­ляется в возникновении на поверхности параллелепипеда касатель­ных напряжений.

Рассмотрим одномерное движение плоского потока в направле­нии оси х. В этом случае касательные напряжения возникают на поверхности                   dF = d х d у верхней и нижней граней параллелепипеда. Причем если на нижней грани касательное напряжение равно t, то на верхней оно будет равно

t +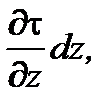

где слагаемое 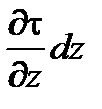   выражает изменение касательного напряжения вдоль  оси z по длине ребра параллелепипеда.

    Проекция равнодействующей сил трения на ось x будет равна

td х d у -  (t + 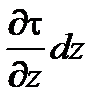)dxdy =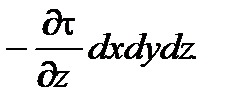

Подставив в это выражение зна­чение рассчитываемого согласно закону Ньютона касательного напряжения t, равного 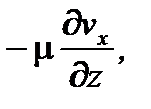получают

 

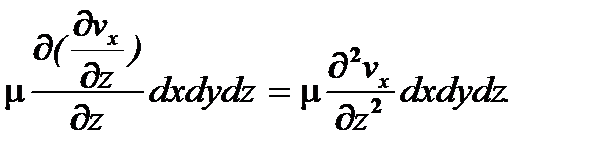
dy

dz

dx

z

y

x

t +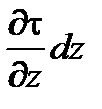

t

О

 

 

Рис. 4.1

 

В случае трехмерного потока составляющая скорости изменя­ется в направлении всех трех осей координат и проекция равнодей­ствующей сил трения на ось х, имеющая вид

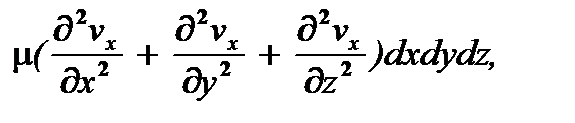
определяется суммой вторых производных по осям координат, где 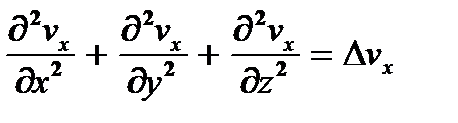- оператор Лапласа.

Сумма проекций сил, действующих на элементарный параллеле­пипед (силы тяжести, гидростатического давления и трения), согласно принципу кинетостатики будет равна

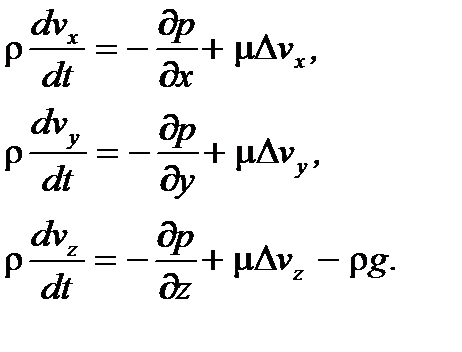                                                    (4.1) 

Субстанциональные производные от скорости по времени в этой системе уравнений для установившегося и неустановившегося потоков определяются выра­жениями (3.6).

В этих уравнениях rg отражает влияние силы тяжести, частные производные др/ ¶ х, др/ду, др/д z характеризуют влияние перепада гидростатического давления, а произведение m на оператор Лапла­са - влияние сил трения на поток жидкости. Левые части уравнений представляют собой проекции равнодействующей силы инерции, т. е. произведение массы единицы объема r на проекцию ее ускорения.

Дифференциальные уравнения Эйлера (3.5) для идеальной жидкости получают, как частный слу­чай при m = 0, из системы уравнений (3.7).

Для полного описания движения реальной жидкости необходимо при выводе системы уравнений учитывать сжимаемость, темпера­турное расширение жидкости, а к описанию добавить дифферен­циальные уравнения неразрывности потока.

Сложность математического аппарата затрудняет решение системы дифференциальных уравнений Навье-Стокса в аналитическом виде. Эта система уравнений количественно  проанализирована  лишь для ряда простейших слу­чаев.

Для решения практических задач принимают обычно ряд упро­щений допущений,   а также используют методы теории подобия.

         Критериальные уравнения вязкой несжимаемой жидкости

Для вывода критериального уравнения, описывающего движе­ние вязкой жидкости, например, в трубопроводе, пользуются дифферен­циальным уравнением Навье-Стокса.

Для одномерного движения потока жидкости вниз, вдоль оси абсцисс, дифференциальное уравнение можно записать так:

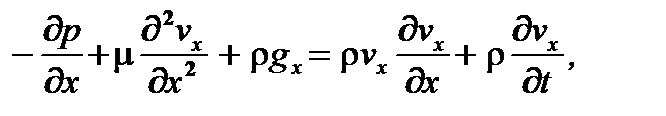                                                     (4.2)

где р - давление; m - динамическая вязкость; v - скорость; r - плотность; t -  время.

Вводя характерные для потока жидкости величины длины - L = d, скорости - V = U и времени - Т= L/V = d/U (где d и U - соответственно, диаметр трубы и расходная скорость потока), в уравнении (4.2) переходят к  безразмерным величинам по формулам

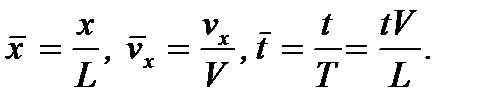
В результате чего, если для простоты опустить черточки над этими величинами, вместо уравнения 4.2) имеют

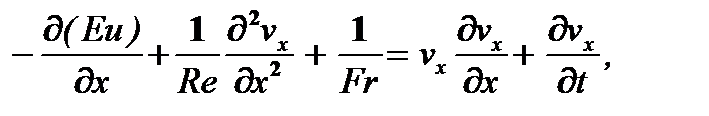                                                  (4.3)

где Eu = p/(rU²) - число Эйлера - отношение сил давления к силам инерции, Re = Udr/m - число Рейнольдса - отношение силы инерции к силам вязкостного трения, Fr = U²/(gd) - число Фруда - отношение сил инерции к силе тяжести.

     Применение критериальных уравнений позволяет, в частности, понизить число определяющих физико-механических и геометрических параметров гидродинамического процесса путем введения безразмерных (критериальных) комплексов (чисел) из этих величин, либо же устанавливать, на базе экспериментов, функциональные зависимости между этими критериями, например, в виде

    Eu = f(Re, Fr),

где f(Re, Fr) – функция, определяемая на основе опытных данных.

Ф ормула расчета силы сопротивления для шара

 Рассматривают задачу о течении вязкой жидкости, вызываемом движением сферы радиуса а, перемещающейся прямолинейно и равномерно со скоростью U . Данная задача, очевидно, эквивалентна задаче об обтекании сферы радиусом а потоком вязкой жидкости, имеющим на бесконечности постоянную по величине и направлению ско­рость U .

В качестве   числа Рейнольдса выбирают

Re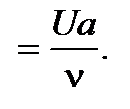

Если число Рейнольдса Re достаточно мало, т. е. для заданной жидкости либо скорость движения сферы достаточно мала, либо радиус сферы очень мал, то применяют приближенный метод решения задачи, а именно, при интегрировании уравнений движения отбрасывают в них инерционные члены.

Среди различных методов решения поставленной задачи одним из наиболее естественных, хотя, может быть, и несколько громоздким, является метод использования сферических координат, который применяется ниже. Очевидно, что, вводя сферические коорди­наты r , J, j, где r - радиус, J - широта j - долгота точки, вследствие симметрии движения относительно оси Ох, от которой отсчитываются углы J, имеют:

    v_r = v_r(r, J), v_J = v_J(r, J), v_j = 0, p = p(r, J).

В таком случае, отбрасывая в  уравнениях движения инерционные члены и полагая, что внешние силы отсутствуют, получают систему уравнений движения жидкости и уравнение неразрывности в сферических координатах:

 

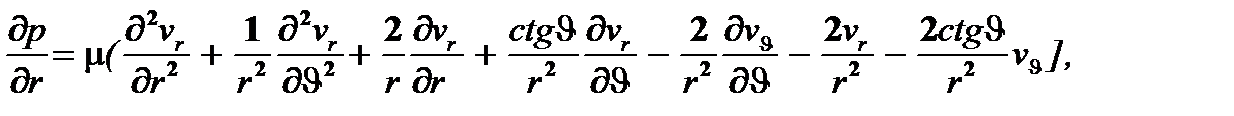
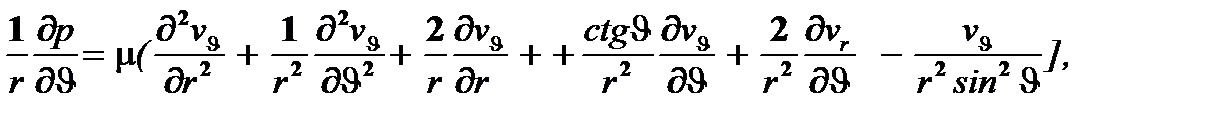             (4.4) 

   

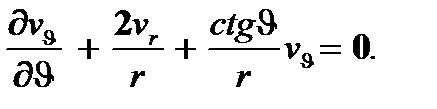
Рассматривая, для определенности, задачу об обтекании покоя­щейся сферы, центр которой находится в начале координат, пото­ком вязкой жидкости, будем, очевидно, иметь следующие граничные условия:

    v_r(a, J) = 0, v_J(a, J) = 0.                                                       (4.5)

Кроме того, считая, что на бесконечности поток имеет направление, параллельное положительной оси Ох, имеют следующие условия на бесконечности:     

v_r ® UCosJ, v_J ® -USinJ при r ® ¥.                                     (4.6)

Вид граничных условий (4.5), (4.6) указывает на то, что решения основных уравнений (4.4) следует отыскивать в форме:

v_r(r, J) = f(r)CosJ, v_J(r, J) = -g(r)SinJ, p(r, J) = mh(r)CosJ.           (4.7)

 

U

-vJ

vr

a

O

J

х

Рис 4.2

В самом деле, простое вычисление показывает, что для трех функ­ций f(r), g(r), h(r) получают из (4.4) три обыкновенных дифференциальных уравнения:

h¢ = f¢¢ + 2f¢/r - 4(f - g)/r²,

h/r = g¢¢ + 2g¢/r + 2(f - g)/r²,                                 (4.8)

f¢ + 2(f - g)/r = 0.

- причем из (4.5) и ( 4.6) вытекают следующие граничные условия:

    f(а) = 0, g(а) = 0, f(¥) = U, g(¥) = U .                             (4.9)

Чтобы решить систему (4.8) из третьего уравнения этой системы  определяют g :

g = f¢r/2 + f.                                                                           (4.10)

После чего из второго уравнения (4.8) с помощью простых дифферен­цирований находят h:

h = f¢¢¢r²/2 + 3r f¢¢ + 2 f¢.                                            (4.11)

И, наконец, первое уравнение (4.8) доставляет дифференциальное уравнение для определения f

r³f^1У + 8r²f¢¢¢ + 8rf¢¢ - 8f¢ = 0.                                      (4.12)

Но это последнее уравнение есть уравнение типа Эйлера и потому легко интегрируется; среди его частных решений всегда существуют решения вида

f = r^k.                                                                              (4.13)

Уравнение (4.12) будет удовлетворяться, если k есть решение уравнения четвертой степени

k (k - 1)(k - 2)(k - 3) + 8k (k - 1)(k - 2)+ 8k (k - 1) - 8k  = 0,

т. е. k должно принимать одно из следующих четырех значений:

k  = 2, k = 0, k = - 1, k   = -3.                             (4.14)

Таким образом, согласно (4.13), (4.14) частными интегралами уравнения (4.12) являются

  

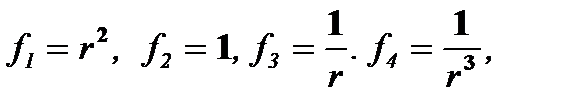
а общим его интегралом будет

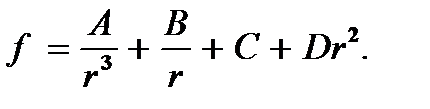                                                      (4.15)

    Уравнения (4.10) и (4.11) дают соответствующие значения g и h:

    g = 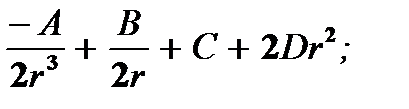h = 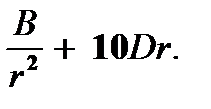                        (4.16)

Постоянные А, В, С и D определяют из граничных условий (4.9), которые дают:

D = 0, C = U , B = -1,5Ua , A = 0,5Ua³.               (4.17)

Подставляя (4.17) в (4.15), (4.16), приходят к следующему решению задачи:

   

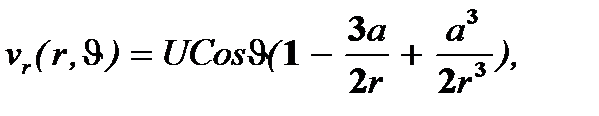
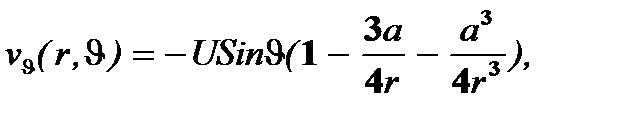                                          (4.18)

   

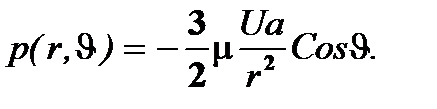
    Используя формулы расчета составляющих тензора напряжений:

   

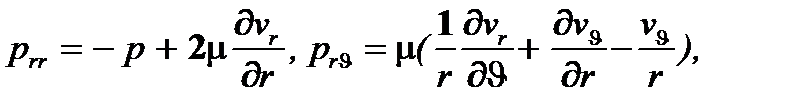
вычисляют силу, с которой поток воздействует на сферу.

    На поверхности сферы v_r = 0, v_J = 0, а,  следовательно, согласно (4.18), и ¶v_r/¶J = 0, ¶v_J/¶J = 0. Кроме того, из последнего уравнения (4.4) вытекает, что  ¶v_r/¶r на поверхности сферы также обращается в нуль, и поэтому предыдущие формулы сильно упрощаются и дают для точек сферы следующие соотношения:

   

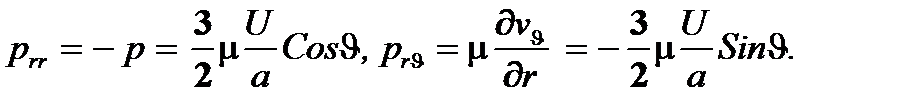
    Поскольку направление равнодействующей всех сил, приложенных к элементам сферы, совпадает с направлением потока на бесконечности, то величина этой равнодействующей определяется формулой

   

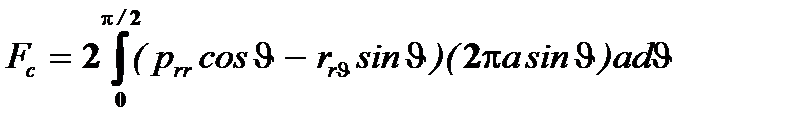
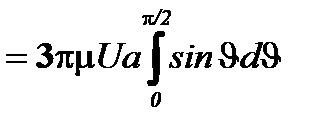
или

    F_c = 6pmU а.                                                                    (4.19)

    Полученное выражение, носящее называние формулы Стокса, играет фундаментальную роль в гидродинамике медленных движений вязкой несжимаемой жидкости.

    Учитывая, что сила сопротивления, обусловленная давлением потока на сферу составляет

       

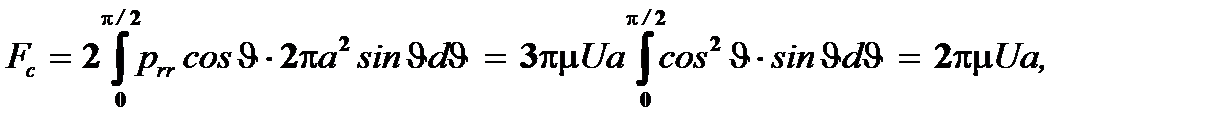
то отсюда вытекает, что ее вклад в силу Стокса в два раза ниже, чем соответствующий вклад за счет сил вязкости.