Гидростатика. Основное уравнение гидростатики
Основное уравнение гидростатики получают из дифференциальных уравнений равновесия жидкости. Рассматривают равновесие жидкости, находящейся в относительном покое. В этом случае на нее действуют массовые силы – силы тяжести и инерции – и поверхностные – сила гидростатического давления. Из всего объема жидкости выделяют элементарный параллелепипед объемом dV .
Ребра параллелепипеда d х, d у, dz располагают параллельно осям х, у, z (рис. 1.1). Среднее значение силы гидростатического давления, действующей на каждую грань со стороны окружающей жидкости, равна произведению гидростатического давления р(х, у, z) на площадь грани параллелепипеда.
Составляют сумму проекций на оси х, у, z всех сил, действующих на элементарный параллелепипед. Если обозначить проекции на оси х, у, z всех, отнесенных к единице массы, массовых сил через X , Y , Z то, например, проекция объемных сил на ось х будет равна Qx = Х d т , где масса жидкости d т = rd х d у dz , или dQx = Хrd х d у dz . Согласно условию равновесия сумма проекций всех сил, действующих на жидкость, в случае покоя равна нулю.
Поэтому сумма проекций сил на ось х
p d у dz - (p + 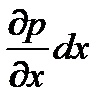 )d у dz + Хrd х d у dz = 0, (2.1)
)d у dz + Хrd х d у dz = 0, (2.1)
где p d у dz - сила гидростатического давления, действующего на левую грань; ¶ p/¶ x - изменение гидростатического давления в данной точке по оси х; 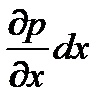 - изменение гидростатического давления по длине ребра d x.
- изменение гидростатического давления по длине ребра d x.
Тогда гидростатическое давление на правую грань будет равно
p + 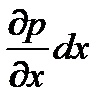 , а проекция средней силы гидростатического давления на ось х (p +
, а проекция средней силы гидростатического давления на ось х (p + 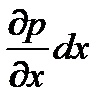 )dydz .
)dydz .
После раскрытия скобок и сокращения на основе выражения (2.1) имеют
- 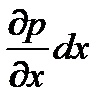 + Хr = 0.
+ Хr = 0.
Аналогично, получают уравнения равновесия по осям y и z
- 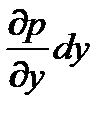 + Yr = 0,
+ Yr = 0,
- 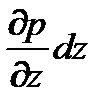 + Zr = 0.
+ Zr = 0.
Или, в совокупности
- 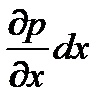 + Хr = 0,
+ Хr = 0,
- 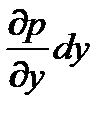 + Yr = 0, (2.2)
+ Yr = 0, (2.2)
- 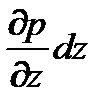 + Zr = 0.
+ Zr = 0.
| y |
| x |
| z |
| Mz+dz |
| p |
| р |
| p gdm |
| р+(¶р/¶х)dx |
| My+dy |
| р+(¶р/¶z)dz |
| р+(¶р/¶y)dy |
Рис. 2.1
Систему уравнений (2.2) полагают в основу расчета гидродинамике.
Гидродинамика
В зависимости от закономерностей движения жидкости различают установившееся и неустановившееся движение.
При установившемся движении скорости v, ускорения частиц жидкости, давления, глубины не меняются во времени (¶v /¶t = 0, ¶р/¶t = 0 и т. д.), а являются только функцией координат, т. е. зависят лишь от положения в потоке жидкости рассматриваемой точки:
v = f1(x,y,z); p = f2(x,y,z),
где v - скорость движения жидкости; р - давление.
При неустановившемся движении скорость и давление потока являются функциями как координат, так и времени:
v = f1(x,y,z, t); p = f2(x,y,z, t).
Установившееся движение потоков характерно для непрерывных процессов, а неустановившееся - для периодических.
Установившееся движение может быть равномерным и неравномерным.
Равномерное движение имеет место, когда скорость, давление, глубина и форма потока не меняются по длине потока. Примером равномерного движения является движение жидкости в трубопроводе постоянного сечения с постоянной скоростью.
Неравномерное движение происходит, например, в конической трубе, когда скорость, давление и глубина потока меняются по длине трубы.
Если рассмотреть поперечное сечение потока жидкости и мысленно представить его состоящим из отдельных элементарных струек, то окажется, что частицы жидкости, находящиеся в струйках, расположенных на различном расстоянии от оси потока, движутся с различными скоростями.
Скорость движения жидкости будет максимальной по оси потока и минимальной в струйках у стенки трубы. Распределение скоростей в потоке зависит от режима движения жидкости.
Уравнение неразрывности потока
Рассматривают зависимость между скоростями в потоке жидкости в условиях неразрывности движения.
Для этого выделяют внутри потока элементарный параллелепипед, объем которого dV = dxdydz (рис. 2.1). Если vx - составляющая скорости вдоль оси х, то тогда через левую грань параллелепипеда площадью dydz за бесконечно малый промежуток времени d t в него войдет масса жидкости, равная (рис. 2.2)
Mx = rvxdydzd t.
| vx |
| y |
| x |
| z |
| Mz+dz |
| My |
| Mx |
| Mz |
| Mx+dx |
| My+dy |
| vz |
| vy |
Рис. 2.2
На противоположной грани параллелепипеда скорость жидкости будет отличаться от скорости на левой грани на величину 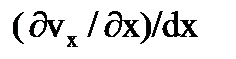 и будет равна
и будет равна
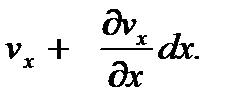
Через правую грань за тот же промежуток времени dt выйдет масса жидкости, равная
Mx + dx = r( 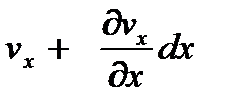 )dydzd t.
)dydzd t.
Приращение массы в параллелепипеде в направлении х будет
dMx = Mx - Mx + dx = -r(¶vx/¶x)dxdydzdt.
Соответственно вдоль осей у и z изменение массы жидкости составит
dMy = My - My+dy = -r(¶vy/¶y)dxdydzdt,
dMz = Mz - Mz+dz = -r(¶vz/¶z)dxdydzdt.
Общее изменение массы жидкости в параллелепипеде за время dt будет равно сумме ее изменений по осям координат:
dM = dMx + dMy + dMz = 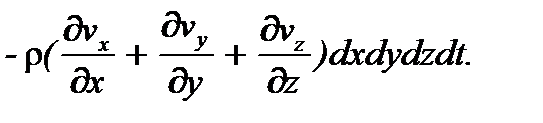 (2.3) Если жидкость несжимаема, т.е. r = с onst, то масса жидкости внутри параллелепипеда должна быть постоянной, а, следовательно, общее изменение массы dM = 0, и поэтому в силу (3.3)
(2.3) Если жидкость несжимаема, т.е. r = с onst, то масса жидкости внутри параллелепипеда должна быть постоянной, а, следовательно, общее изменение массы dM = 0, и поэтому в силу (3.3)
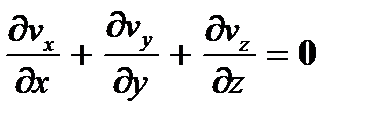 , (2.4)
, (2.4)
где 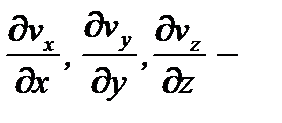 изменение скорости в направлении осей х, у, z .
изменение скорости в направлении осей х, у, z .
Это уравнение называют дифференциальным уравнением неразрывности потока несжимаемой жидкости или уравнением сохранения массы.
Дата: 2019-02-02, просмотров: 353.