Курс лекций
по дисциплине « Физико -химические основы и общие принципы переработки растительного сырья ) »
Федеральное агенство по образованию
ГОУ ВПО «Московский государственный университет технологий и управления им. К.Г. Разумовского»
Кафедра технологии переработки растительного сырья и парфюмерно-косметических изделий
Курс лекций
по дисциплине «Технология комплексной переработки перспективных видов углеводесодержащего сырья (Сахар)»
Москва
ГОУ ВПО «МГТУ им. К.Г. Разумовского»
2015
Составители: д-р техн. наук Е.В. Семенов,
д-р техн. наук А.А. Славянский
Курс лекций по дисциплине «Физико-химические основы и общие принципы переработки растительного сырья»/Сост.: Е.В. Семенов, А.А. Славянский – М.: ГОУ ВПО «МГТУ им. К.Г. Разумовского», 2015.
В работе, в рамках законов механики твердого тела и механики сплошной среды, исследуются связанные с инженерной деятельностью специалиста пищевой промышленности вопросы равновесия и движения жидкостных и газообразных сред растительного происхождения. Рассматриваются вопросы приложения данных законов к анализу кинетики взвесей из продовольственного сырья и пищевых продуктов в технологических процессах пищевых производств.
Для студентов бакалавриата и магистратуры специальности 151000, направление «Технологические машины и оборудование», профиль «МАПП»
квалификация (степень) выпускника: бакалавр
Ó ФГБОУ ВПО «Московский государственный университет технологий и управления имени К.Г. Разумовского», 2015
ОГЛАВЛЕНИЕ
Лекция 1. Предмет курса. Цели и задачи изучаемого курса. . .5
Лекция 2. Гидромеханические процессы. Гидростатика.
Основное уравнение гидростатики. Гидродинамика. Уравнение неразрывности потока. . . . . . . . . .6
Лекция 3. Уравнения Эйлера динамики идеальной жидкости. Уравнение Бернулли и его приложения в технике. . . . . .10
Лекция 4. Основы теории динамики вязкой несжимаемой жидкости.
Дифференциальные уравнения движения вязкой несжимаемой жидкости (уравнения Навье-Стокса). Критериальное моделирование гидромеханических процессов. Формула расчета силы сопротивления для шара.. .12
Лекция 5. Количественный анализ процесса разделения смеси частиц растительного происхождения в пневмосепарирующем канале. . .18
Лекция 6. Исследование процесса сепарирования жидкостных систем биологического происхождения. . . . . . . . 27
Лекция 7. Количественный анализ эффективности процесса центрифугирования суспензий. . . . . . . . .33
Лекция 8. Фильтрование жидкостных систем растительной
природы. . . . . . . . . . . .39
Лекция 2. Гидромеханические процессы. Гидростатика.
Лекция 8. Фильтрование жидкостных систем
Растительной природы
Фильтрованием в производствах АПК называют такой механический процесс, когда разделение гетерогенной жидкостной системы биологического происхождения осуществляют при помощи пористой перегородки. Путем фильтрования проводят первичную обработку молока, посол сыров, брынзы, мясных продуктов, подвергают регенерации солевые растворы, осуществляют пропитку фруктов сиропами, отводят раствор сахара из утфеля, обезвоживают осадки сточных вод и другое. В настоящее время в связи с созданием перегородок мембранного типа с диаметром отверстий порядка величины молекул жидкости появилась возможность использовать фильтрование как процесс выделения из жидкости весьма высокой дисперсности (гиперфильтрование), в том числе и клеточных организмов в микробиологическом производстве.
Фильтрование суспензий является одним из сложных процессов, зависящим от большого числа геометрических и физико-химических параметров, что препятствует адекватному обоснованию математического моделирования фильтрования. До сравнительно недавнего времени основным подходом к решению проблем фильтрования суспензий биологического происхождения считается гидравлический, когда в основу анализа конкретных задач полагают закон сохранения массы (уравнение неразрывности) и феноменологические соотношения типа закона Дарси или других. Наряду с гидравлическим, за последние годы все более широкое распространение получает подход, основанный на использовании фундаментальных уравнений механики многокомпонентных взаимопроникающих сред в совокупности с уравнениями фильтрационной консолидации. Такой подход условно считают гидродинамическим.
Решающую роль в процессе фильтрования играют свойства подвергаемых разделению биологических жидкостей, такие как плотность, вязкость, химическая активность, а также такие факторы как крупность и форма частиц и их электрокинетические свойства. Помимо этого, существенное влияние на процесс фильтрования оказывает такой параметр как объемная концентрация твердого в суспензии. В зависимости от степени концентрации твердой фазы в жидкостной смеси различают следующие виды фильтрования: с образованием осадка, промежуточное, с закупориванием пор осадком, с постепенным, а также полным закупориванием пор фильтровальной перегородки. Постепенное, либо полное закупоривание пор фильтрующих элементов обычно наблюдают при фильтровании мало концентрированных суспензий, тогда как фильтрование с образованием осадка имеет место при разделении суспензий со средним и высоким уровнем концентрации твердого.
Образующиеся при фильтровании суспензий осадки представляют собой весьма сложную многокомпонентную систему, структура которой состоит из различающихся по своей природе размерам и форме твердых частиц (твердая фаза), жидкости, пузырьков газа (жидкая и газовая фазы). В зависимости от размеров частиц, составляющих осадок, твердые частицы в большей или меньшей степени подвержены действию внешних и внутренних сил. Внутренние силы обусловливают связи между дисперсными частицами и агрегатами из этих частиц. Согласно классификации, данной акад. П.А. Ребиндером, образованные в процессе фильтрования связи относят к коагуляционным, конденсационно-кристаллизационным или смешанным коагуляционно-кристаллизационным. Если прочность коагуляционных структур, образованных в высокодисперсных суспензиях, обусловлена ван-дер-ваальсовыми силами сцепления, сравнительно невелика, то после разрушения этих структур и перехода их в коагуляционно-кристаллизационные, получают механические системы с прочными связями, обладающими способностями пластических сред.
Поскольку структура осадков является весьма сложной, то проводить анализ процесса фильтрования на основе обычных методов гидродинамики не представляется возможным. В связи с этим при исследовании процесса фильтрования вводят те или иные отражающие общие статистические закономерности осредненные характеристики, справедливые для достаточно больших объемов осадка. Несмотря на то, что из-за сложности структуры осадка его невозможно описать адекватно набором конечного числа параметров, для конкретных инженерных задач фильтрования оказывается достаточно небольшого числа осредненных характеристик, отражающих в целом свойства осадка.
В качестве осредненных параметров, описывающих характеристики осадка, принимают пористость В, проницаемость k или обратную ей величину - удельное сопротивление осадка. В предположении, что структура слоя осадка описана какой-либо одной из геометрических моделей, а осадок несжимаем, получают ту или иную эмпирическую зависимость, связывающую пористость осадка с его проницаемостью (формула Козени-Кармана или др.). Если осадок сжимаемый, то исходя из геометрических моделей осадка получают соответствующие более сложные функциональные зависимости пористости осадка от его проницаемости.
Если в качестве основных гидравлических характеристик потока жидкости при фильтровании принимают скорость фильтрации v (как осредненную по объему жидкости), то при анализе задач фильтрования суспензий биологического происхождения используют эмпирический закон фильтрации в форме, предложенной Дарси. Этот закон эффективно применяют при исследовании ламинарных потоков жидкостей ньютоновского типа в практически несжимаемых пористых средах таких, например, как крупнозернистый песок.
Фильтрование суспензии в сферическом пласте
Исследуется напорное осесимметричное фильтрование двух несжимаемых жидкостей в одно - и двухслойном пласте сферической формы при наличии границы, разделяющей жидкости, а также при наличии промежуточной зоны - области совместного движения жидкости. Предполагают, что внутри пористого сферического изотропного и однородного пласта под действием постоянного перепада давления одна жидкости вытесняет другую, не смешиваясь, и пусть пласт дренируется расположенной в центре сферы дреной. Предполагают также, что режим пласта упругий, и, кроме того, справедлив закон фильтрации Дарси. Пусть В (0 < В < 1) - пористость сферы, k - проницаемость, R - радиус сферы, ограничивающей пористую среду, r0 - радиус совершенной дрены, ri (i = 1,2) - соответственно, динамическая вязкость и плотность жидкостей (рис. 8.1).
| R |
I II
| x |
O
| r0 |
Рис. 8.1
Требуется найти уравнение поверхности раздела r = x(t) в предположении, что режим фильтрования осесимметричный. В пищевой промышленности эта задача связана с анализом процесса принудительного посола молочных продуктов, пропитки фруктов сиропом под давлением и другим.
В принятом допущении о линейном характере процесса фильтрования скорости фильтрации для зоны нагнетания (i = 1) и зоны вытеснения (i = 2) согласно закону Дарси равны
vi = -(k/mi)¶pi/¶r, (8.1)
где vi, pi - соответственно, скорость фильтрации и давление в i - той зоне.
Поскольку, с точностью до постоянного множителя, при осесимметричном режиме, расход жидкости через сферическую поверхность r = r в пористом пласте равен 4pr2v и зависит только от времени, то вследствие закона сохранения масс, для каждой из жидкостей в сферических координатах имеют ¶(vir2)/(¶r) = 0, откуда заключают, что
vir2 = hi(t), (8.2)
где hi(t) = произвольная функция времени. Тогда в силу (6.1), (6.2) находят
¶pi/¶r = -[mi/(kr2)] hi(t), (8.2)
pi = mi/(kr)hi(t) + gi(t), (8.4)
где gi(t) - произвольная функция времени. Если значения давления на поверхностях сферы r = R и дрены r = r0 соответственно Р1 и Р2, то имеют граничные условия
р = Р1 при r = R, (8.5)
р = Р2 при r = r0, (8.6)
Кроме того, учитывая равенство давлений р1, р2 и скоростей фильтрации v1, v2 на границе раздела жидкостей r = x(t), исходя из (6.1), получают
Р1 = р2, m2¶р1/¶r = m1¶р2/¶r при r = x(t). (8.7)
Тогда в силу (6.3) - (6.7) имеют систему
m1/(kR)h1(t) + g1(t) = P1, m2/(kR)h2(t) + g2(t) = P2,
(8.8)
m1/(kx)h1(t) + g1(t) = m2/(kx)h2(t) + g2(t), h1(t) = h2(t).
Решением системы уравнений (6.8) является
h1(t) = h2(t) =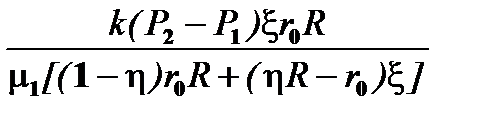 
, (8.9)
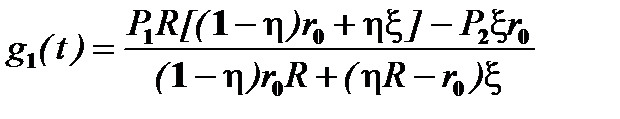, (8.10) 
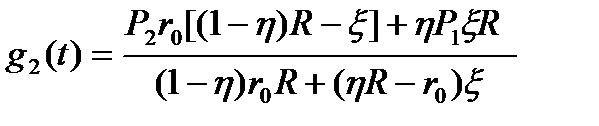, (6.11)
где h = m2/m1. В допущении, что Р1 > P2, r0 < x < R, исходя из (6.9), заключают, что h1(t) < 0, то есть, поток жидкости является сходящимся.
Таким образом, в соответствии с (6.4), (6.9) - (6.11) имеют
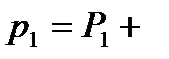
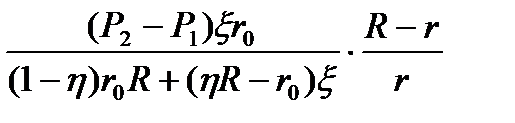
(8.12)
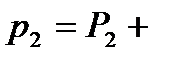
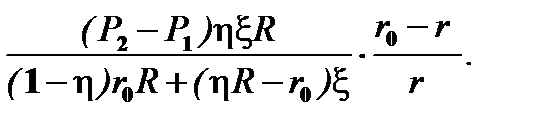
Принимая во внимание кинематическое условие на поверхности раздела двух жидкостей
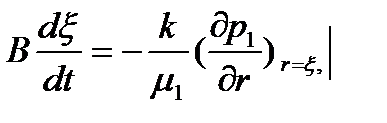(8.13)
в силу (6.12) получают
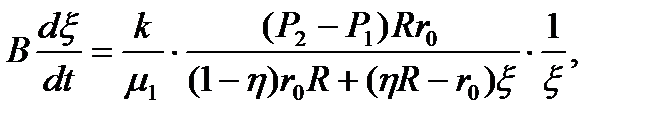
откуда, разделяя переменные, имеют
[(1 - h)r0Rx + (hR - r0)x2]dx = k/(Bm1)×(P2 - P1)r0Rdt. (8.14)
Интегрируя (6.14) слева в пределах от R до x, справа - в пределах от 0 до t, получают
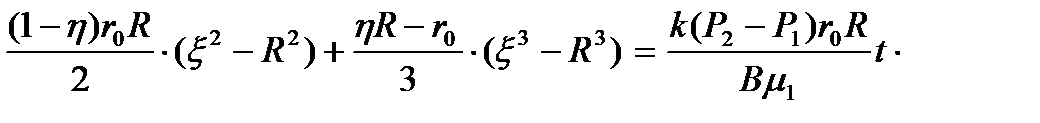(8.15)
Соотношение (6.15) представляет собой алгебраическое уравнение третьей степени, которое в принципе можно разрешить явно относительно x = x(t). Если в (6.15) положить x = r0, то время полного вытеснения первой жидкостью второй составит
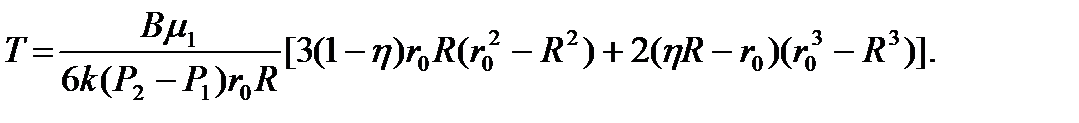(8.16)
Из (6.16) следует, что при Р1®Р2 время полного вытеснения Т®µ. Если имеют две жидкости разной плотности и одинаковой вязкости (что соответствует, например, случаю вытеснения соленой водой пресной воды), то есть, m1 = m2 = m, h = 1, то вследствие (6.15) уравнение движения границы имеет вид
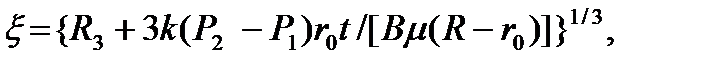
а время полного вытеснения
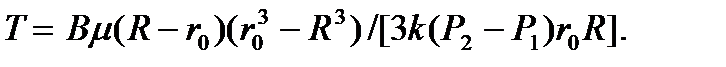
Если вязкость первой жидкости значительно больше вязкости второй, то есть, m1 = m >> m , h®0, что соответствует, например, случаю пропитки концентрированным сахарным сиропом плодов сферической формы, то исходя из (6.15), (6.16) получают
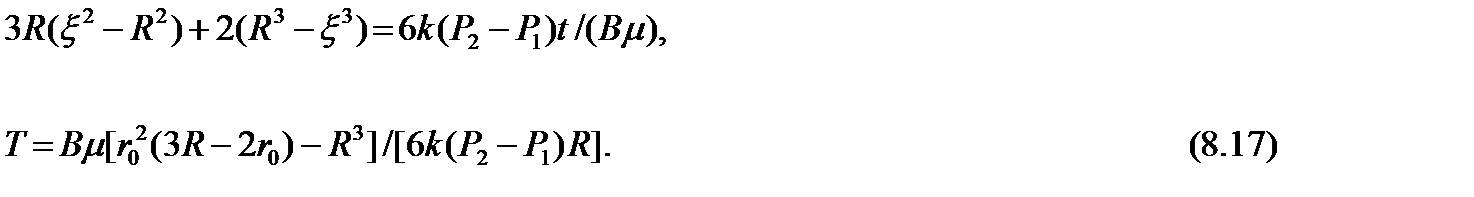Расчет периода полного вытеснения одной жидкостью другой согласно (6.17), для значений параметров R = 0,05м, r0 = 0.01м, m = 0,01Па×с, k = 10-14м2, DР =Р2 - Р1 = 10-6 Па, В = 0,9 дает величину Т = 336 с.
Уточненный расчет по формуле (6.15) для значений параметров режима фильтрования с вытеснением одной жидкостью другой в сферическом пласте R = 0,05м, r0 = 0,01м, m = 0,01Па×с, h = 0.1, k = 10-14 м2, DР = 10-6 Па, m = 0,9 дает для времени полного вытеснения Т = 3576 с или примерно Т = 1 ч.
СПИСОК ЛИТЕРАТУРЫ
1. Кавецкий Г.Д., Касьяненко В.П.. Процессы и аппараты пищевой технологии. - М:”КОЛОС”. - 2008. - 591 с.
2. Лыков А.В. Теория теплопроводности. - М.: Высшая школа. 1967. 600 с.
3. Семенов Е.В., Акулов Н.И., Журба О.С., Карамзин А. В. Количественное моделирование процессов массопереноса в перерабатывающих производствах АПК. - М.: CПУТНИК+. - 2006. - 286 с.
4. Семенов Е.В., Карамзин В. А., Карамзин А. В. Методы расчета технологических процессов массо- и теплопереноса перерабатывающих отраслей АПК. - М.: CПУТНИК+. - 2009. - 211 с.
5. Семенов Е.В., Карамзин В. А.,. Карамзин А. В., Славянский А.А. Количественное моделирование технологических инноваций в перерабатывающих производствах АПК. - М.: CПУТНИК+ . - 2012. - 224 с.
6. Славянский А.А. Сахар: назначение, свойства и производство. Учебное пособие. Изд-во МГУТУ «Московский государственный университет технологий и управления имени К.Г. Разумовского». - 2012. - 214 с.
7. Семенов Е.В., Славянский А.А. Моделирование процессов кристаллизации и центрифугирования - М.: CПУТНИК+. - 2015. - 217 с.
Курс лекций
по дисциплине «Технология комплексной переработки перспективных видов углеводесодержащего сырья (Сахар)»
Составители: СЕМЕНОВ Евгений Владимирович,
СЛАВЯНСКИЙ Анатолий Анатольевич
Вопросы к зачету по курсу
« Физико -химические основы и общие принципы переработки растительного сырья ) »
1. Предмет курса. Цели и задачи изучаемого курса. Обзор основных, используемых при прохождении курса, теоретических положений дисциплин - высшей математики, физики и теоретической механики.
2. Гидромеханические процессы. Гидростатика. Основное уравнение гидростатики.
3. Гидродинамика. Общие положения.
4. Уравнение неразрывности потока.
5. Основы теории динамики вязкой несжимаемой жидкости. Критериальное моделирование гидромеханических процессов.
6. Формула расчета силы сопротивления для шара.
7. Количественный анализ процесса разделения смеси частиц растительного происхождения в пневмосепарирующем канале.
8. Анализ кинематики частицы в пневмосепарирующем канале при числе Рейнольдса Re < 1.
9. Постановка задачи о кинематике частицы в пневмосепарирующем канале при числе Рейнольдса Re > 1. Как развивается процесс пневмосепарирования при разделении зерносмеси?
10. Исследование процесса сепарирования жидкостных систем биологического происхождения. Постановка задачи. Где имеют место данные процессы в сахарной промышленности?
11. Осаждение частиц в условиях свободного отстоя при малых значениях числа Рейнольдса. Расчет скорости и времени осаждения частицы. Где встречаются процессы свободного отстоя в сахарной промышленности?
12. 
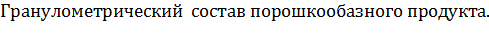Массовые функция распределения и характеристичекая функция распределения частиц по крупности. Где и для чего используют 
продукта в сахарной промышленности?
13. Понятие текущего и глобального критического диаметра частицы. Где и для чего используют понятие критического диаметра частицы
при количественном анализе процессов в сахарной промышленности?
14. Коэффициент уноса и коэффициент осветления при обработке суспензии. В чем состоит смысл этих понятий применительно к сахарному производству?
15. Осаждение частиц в центробежном силовом поле. Расчет скорости и времени осаждения частицы в данном силовом поле при малых значениях числа Рейнольдса. Каковы основные физико-механические факторы, влияющие на эффективность процесса осаждения кристаллов сахарозы?
16. Центрифуга периодического действия. Где и с какой целью применяются центрифуги периодического действия в сахарной промышленности? Каковы основные физико-механические и геометрические параметры данных центрифуг?
17. Силы, действующие на частицу в роторе центрифуги непрерывного действия. Расчет скорости осаждения частицы в роторе центрифуги непрерывного действия. Зачем нужен этот расчет?
18. Расчет критического диаметра для потока суспензии в роторе центрифуги непрерывного действия. Где и с какой целью применяются центрифуги непрерывного действия в сахарной промышленности? В чем состоит различие процессов разделения утфеля в центрифугах периодического и непрерывного действия?
19. Фильтрование жидкостных систем в продуктах растительного происхождения. Закон Дарси. В чем состоит механический смысл данного закона? В каких производствах сахарной промышленности имеют место процессы фильтрования?
20. Пропитка плодов шарообразной формы сахарным раствором.
Утверждено на заседании кафедры технологии переработки растительного сырья и парфюмерно-косметических изделий МГУТУ им. К.Г. Разумовского
Зав. кафедрой, профессор (Славянский А.А.)
Уважаемая Светлана!
Высылаю Вам и вашим студентам перечень вопросов по курсу "Физико-химические основы отрасли":
1. Какие физико-химические процессы протекают в технологическом потоке производства сахара на сахарном заводе.
2. Какие изменения претерпевает исходное сахарсодержащее сырье по этапам обработке его на сахарном заводе.
3. Каковы цели процесса получения товарного сахара.
4. Что является движущей силой процесса обессахаривания свекловичной стружки.
5. Как работает диффузионный аппарат при обработке свекловичной стружки.
6. Какие физико-механические и геометрические параметры свекловичной стружки Вам известны.
7. Что и зачем производит ТЭЦ на сахарном заводе.
8. Как работают выпарные установки (ВУ).
9. Для каких целей используют выпарные установки.
10. Каковы этапы обработки сахара в продуктовом отделении.
11. В чем отличие процессов, протекающих в ВУ и вакуум-аппарате.
12. Что происходит с межкристальным раствором в процессе кристаллообразования
в вакуум-аппарате.
13. Какой раствор называют метастабильным.
14. Что инициирует начало процесса кристаллообразования.
15. С какой целью используют «затравку».
16. Зачем утфель "раскачивают".
17. Зачем утфель размешивают.
18. Какие условия начала и развития процесса кристаллизации.
19. Что такое гетерогенная жидкостная система.
20. Какими параметрами характеризуется суспензия типа сахарный утфель.
21. Что такое 1-ый, 2-ой и 3-тий продукты в процессе получения сахара-песка.
22. Как поступают с оттеками при обезвоживании межкристального раствора.
23. Что входит в состав несахаров.
24. С какой целью эксплуатируют центрифуги в продуктовом отделении сахарного завода.
25. Что такое поток концентрации.
26. Какова движущая сила процесса молекулярной диффузии.
27. Сформулируйте первый закон Фика.
28. Какие переменные величины связывает первый закон Фика.
29. Сформулируйте второй закон Фика. В чем его физический смысл.
30. Сформулируйте начальное и граничные условия по концентрации сахарозы
для уравнения конвективной диффузии.
31. Для чего используют решение уравнения конвективной диффузии.
Курс лекций
по дисциплине « Физико -химические основы и общие принципы переработки растительного сырья ) »
Федеральное агенство по образованию
ГОУ ВПО «Московский государственный университет технологий и управления им. К.Г. Разумовского»
Кафедра технологии переработки растительного сырья и парфюмерно-косметических изделий
Курс лекций
по дисциплине «Технология комплексной переработки перспективных видов углеводесодержащего сырья (Сахар)»
Москва
ГОУ ВПО «МГТУ им. К.Г. Разумовского»
2015
Составители: д-р техн. наук Е.В. Семенов,
д-р техн. наук А.А. Славянский
Курс лекций по дисциплине «Физико-химические основы и общие принципы переработки растительного сырья»/Сост.: Е.В. Семенов, А.А. Славянский – М.: ГОУ ВПО «МГТУ им. К.Г. Разумовского», 2015.
В работе, в рамках законов механики твердого тела и механики сплошной среды, исследуются связанные с инженерной деятельностью специалиста пищевой промышленности вопросы равновесия и движения жидкостных и газообразных сред растительного происхождения. Рассматриваются вопросы приложения данных законов к анализу кинетики взвесей из продовольственного сырья и пищевых продуктов в технологических процессах пищевых производств.
Для студентов бакалавриата и магистратуры специальности 151000, направление «Технологические машины и оборудование», профиль «МАПП»
квалификация (степень) выпускника: бакалавр
Ó ФГБОУ ВПО «Московский государственный университет технологий и управления имени К.Г. Разумовского», 2015
ОГЛАВЛЕНИЕ
Лекция 1. Предмет курса. Цели и задачи изучаемого курса. . .5
Лекция 2. Гидромеханические процессы. Гидростатика.
Основное уравнение гидростатики. Гидродинамика. Уравнение неразрывности потока. . . . . . . . . .6
Лекция 3. Уравнения Эйлера динамики идеальной жидкости. Уравнение Бернулли и его приложения в технике. . . . . .10
Лекция 4. Основы теории динамики вязкой несжимаемой жидкости.
Дифференциальные уравнения движения вязкой несжимаемой жидкости (уравнения Навье-Стокса). Критериальное моделирование гидромеханических процессов. Формула расчета силы сопротивления для шара.. .12
Лекция 5. Количественный анализ процесса разделения смеси частиц растительного происхождения в пневмосепарирующем канале. . .18
Лекция 6. Исследование процесса сепарирования жидкостных систем биологического происхождения. . . . . . . . 27
Лекция 7. Количественный анализ эффективности процесса центрифугирования суспензий. . . . . . . . .33
Лекция 8. Фильтрование жидкостных систем растительной
природы. . . . . . . . . . . .39
Лекция 1. Предмет курса. Цели и задачи изучаемого курса
Предмет курса
Гидромеханические (жидкостные) процессы. Под «жидкостью» понимают все тела, для которых характерно свойство текучести, т.е. способность сколь угодно сильно изменять свою форму под действием сколь угодно малых сил. Таким образом, в это понятие включают как жидкости обычные, называемые капельными, так и газы.
Первые отличаются тем, что в малых количествах принимают сферическую форму, а в больших обычно образуют свободную поверхность.
Важной особенностью капельных жидкостей является то, что они ничтожно мало изменяют свой объем при изменении давления, поэтому их обычно считают несжимаемыми. Газы, наоборот, способны к весьма значительному уменьшению своего объема под действием давления и к неограниченному расширению при отсутствии давления, т. е. газы обладают большой сжимаемостью.
Несмотря на это различные законы движения капельных жидкостей и газов при определенных условиях можно считать одинаковыми. Основным из этих условий является малое значение скорости течения газа по сравнению со скоростью распространения в нем звука. В гидравлике изучают движения главным образом капельных жидкостей, причем в подавляющем большинстве случаев последние рассматривается как несжимаемые. Что же касается внутренних течений газа, то их относят к области гидравлики лишь в тех случаях, когда скорости их течения значительно меньше скорости звука и, следовательно, сжимаемостью газа можно пренебречь.
Такие случаи движения встречаются на практике довольно часто. Это, например, течение воздуха в вентиляционных системах и некоторых других газопроводах. В дальнейшем изложении под термином «жидкость» понимают капельную жидкость, а также газ, когда его можно считать несжимаемым.
Вследствие трудностей решения задач гидромеханики историческое развитие механики жидкостей шло двумя различными путями.
Первый (теоретический) путь базируется на точном математическом анализе основанных на законах механики явлений в жидкостях. Он привел к созданию теоретической гидромеханики, которая долгое время являлась самостоятельной дисциплиной, непосредственно несвязанной с экспериментом. Хотя метод теоретической гидромеханики является весьма эффективным средством научного исследования, однако он не всегда дает ответы на выдвигаемые практикой вопросы.
Второй путь – путь широкого привлечения эксперимента и накопления опытных данных для использования их в инженерной практике, приведший к созданию гидравлики, возник из насущных задач практической инженерии.
В начальный период своего развития гидравлика была наукой чисто эмпирической. В настоящее время в гидравлике, где это возможно и целесообразно, все больше применяют методы теоретической механики для решения отдельных задач, а в теоретической гидромеханике все чаще прибегают к эксперименту.
| Целый ряд крайне трудно поддающихся теоретическому анализу явлений, ввиду своей сложности, исследуют экспериментальным путем, а результаты такого исследования представляют в виде эмпирических формул. Гидравлика дает методы расчета и проектирования разнообразных гидротехнических сооружений (плотин, каналов, водосливов, трубопроводов для подачи всевозможных жидкостей), гидромашин (насосов, гидротурбин, гидропередач), а также других гидравлических устройств, применяемых во многих областях техники. Особенно велико значение гидравлики в машиностроении, где приходится иметь дело с закрытыми руслами (например, трубами) и напорными течениями в них, т. е. с потоками без свободной поверхности и с давлением, отличным от атмосферного. Гидросистемы, состоящие из насосов, трубопроводов, различных гидроагрегатов, широко используют в машиностроении в качестве системы жидкостного охлаждения, топливоподачи, смазки и др. В различных современных машинах все более широкое применение находят гидропередачи (гидроприводы) и гидроавтоматика. Гидропередачи представляют собой устройства для передачи механической энергии и преобразования движения посредством жидкости. По сравнению с другими видами передач (зубчатыми и. т. п.) гидропередачи имеют ряд существенных преимуществ: простота преобразования вращательного движения в возвратно-поступательное, возможность плавного (бесступенчатого) изменения соотношения скоростей ведущего и ведомого звена, компактность. |
К гидромеханическим относят также и процессы перемешивания в жидких средах, разделения суспензий и эмульсий путем отстаивания, фильтрования, центрифугирования, псевдоожижения зернистого материала и др.
Цели и задачи изучаемого курса
В методической разработке для студентов бакалавриата и магистратуры технологического профиля пищевых производств имеют целью как, в рамках законов механики твердого тела и механики сплошной среды, исследуются связанные с инженерной деятельностью специалиста пищевой промышленности вопросы равновесия и движения жидкостных и газообразных сред растительного происхождения. В качестве задач курса рассматриваются вопросы приложения данных законов к анализу кинетики взвесей из продовольственного сырья и пищевых продуктов в технологических процессах пищевых производств.
Дата: 2019-02-02, просмотров: 352.
