Пусть имеют взвесь из мелких (порядка микрона) высокодисперсных однородных частиц, разного размера и формы, не сильно отличающейся от сферической, счетная функция распределения частиц которой по размеру имеет вид (рис. 6.1)
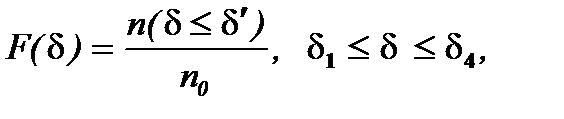(6.1)
где n(d £ d¢) - количество частиц в порошке размером меньше d¢, n0 -количество частиц всех размеров в порошке, d1, d4 - соответственно, наименьший и наибольший из размеров частиц в порошке.
Ставится задача: определить количество частицы, оседающих на дне канала в течение заданного периода времени, имея в виду, что относительное содержание частиц в порошке рассчитывается по зависимости
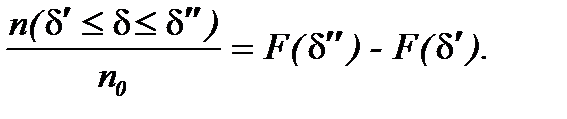
В дальнейшем количество частиц в некоторой среде относят к единице объема среды, т.е. принимают в качестве n счетную концентрацию размерностью 1/м3.
| F, Ф |
| d |
| F |
| Ф |
| 1 |
| 0 |
| d¢ |
| F(d¢) |
Рис. 6.1
Для того чтобы обосновать расчета результатов разделения жидкостной системы необходимо располагать аппаратом количественного анализа процесса разделения в силовом поле полидисперсной жидкостной системы по некоторым статистическим и интегральным показателям дисперсности. В качестве таких показателей выбирают выражения функции распределения (или характеристической функции) а также коэффициентов осветления (и уноса) в зависимости от вида дисперсии частиц в исходном порошке [94].
Интегральные показатели дисперсности взвеси, оседающей в условиях свободного отстоя при малых значениях числа Рейнольдса
Пусть исследуемая смесь «жидкость+твердое» представляет собой высокодисперсную равномерно перемешанную суспензию, гранулометрический состав твердой фазы которой определяется по (6.1). И пусть х - вертикальная координата, h - толщина неподвижного слоя жидкости, в котором изучается изменение по координате и по времени характеристической функции Ф = 1 - F (рис. 4.2), где F задана по (6.1). Причем, вероятностный смысл функции Ф аналогичен (4.1):
Ф(d) =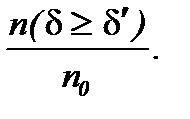 
(6.2)
В таком случае, если сила сопротивления движению частицы диаметром d рассчитывается согласно формуле Стокса, то скорость v ее осаждения
v = (1/k1)d2, (6.3)
где
k1 = 18m/(gD), (6.4)
m - динамическая вязкость жидкости; g - ускорение свободного падения; D = rт - rж > 0; rт, rж - соответственно, плотность твердой фазы и жидкости.
| Fc, FАр |
| О |
| х |
| h |
| h-x |
| v |
| G |
| dx |
Рис. 6.2
Тогда в качестве диаметра d(x,t) частицы, проходящей путь (h - x) со скоростью v (6.3), за время t, т.е. так называемого текущего критического диаметра частицы, принимают
d(x,t) = [k1(h - x)/t]1/2, (6.5)
где k1 находят по (6.4).
Геометрический смысл величины d(x,t) состоит в том, что частицы размером d > d(x,t) опускаются на дно канала за время t¢ < t .
Очевидно, что рассчитываемое по (6.5) значение критического (глобального) диаметра частицы не превышает величины
dк (t) = [k1h/t]1/2. (6.6)
В таком случае из элементарного слоя жидкости с координатой х, единичной площадью и высотой dx (рис. 6.2), за время t выпадет в осадок количество частиц dn дисперсной фазы, равное
dn(x,t) = (n0/h)Ф(d(x,t))dx, (6.7)
где d(x,t) вычисляется по (6.4), Ф - по 6.2.
Интегрируя далее (6.7) по х в пределах от х = 0 до х = h, получают количество частиц, оседающих на дне канала из заданного объема, за период времени t
n1(t) = (n0/h)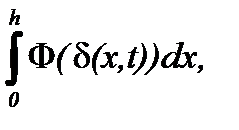 
или, c учетом явной зависимости (6.5)
n1(t) = (n0/h)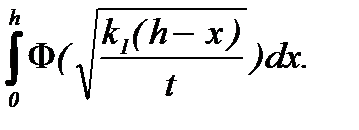 
(6.8)
Проводя в (6.8) замену переменной
h - x = hx, dx = - hdx,
приходят к выражению так называемого счетного коэффициента осветления как функции времени t
h(t) = n1(t)/n0 =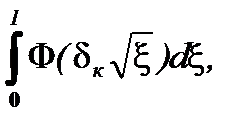 
(6.9)
где dкр определяют по (6.6), x - безразмерное расстояние, выраженное в долях высоты канала h.
Для того чтобы интенсифицировать осаждение в жидкости взвеси, как составной части процесса классификации частиц, данный процесс обычно реализуют в центробежных машинах - центрифугах и сепараторах. При этом процесс осаждения взвеси в роторе центрифуге периодического действия считают естественным аналогом процесса седиментации частиц в условиях свободного отстоя. Причем, формально считают, что в центрифуге кинетика процесса осаждения взвеси обусловлена не полем силы тяжести, а центробежным силовым полем.
В частности, к центрифугам периодического действия относят переносную лабораторную клиническую (стаканчиковую) центрифугу с частотой вращения до 3000 об/мин (50 рад/с), предназначенную для разделения неоднородных жидких систем плотностью до 2 г/см3 в поле центробежных сил.
Интегральные показатели взвеси, седиментирующей
в центрифуге периодического действия
В дальнейшем, в целях обоснования математической модели процесса, предполагают, что ротор центрифуги приведен во внезапное вращательное движение с угловой скоростью w, а ограниченный областью r0 £ r £ R (где r0 и R, соответственно, радиус свободной поверхности жидкости и радиус ротора) поток движется как квазитвердое тело (рис. 6.3). При этом показано, что интродуцированная в данный поток частица небольшого размера движется практически по радиусу с небольшой скоростью.
| w |
| r0 |
| r |
| o |
R
Рис. 6.3
Для того чтобы обосновать выражение текущего критического диаметра тонкодисперсной частицы, формально, силу тяжести G заменяют центробежной силой
Fцб = Vrтw2r,
где r - радиальная координата, и, в таком случае согласно принципу Даламбера записывают
Fцб + FАр + Fc = 0, (6.10)
где FАр, Fc - соответственно, сила Архимеда и сила сопротивления.
Если, для определенности, принимать rт > rж, то в проекции на радиальное направление, уравнение (6.10) принимает вид
VDrw2r + Fc = 0. (6.11), где Dr = rт - rж > 0.
При этом для исследуемого кинетического процесса выражение силы сопротивления Fc выбирают в зависимости от величины числа Рейнольдса Re. Для значений Re < 1 полагают, что Fc, согласно формуле Стокса, пропорционально первой степени величины местной скорости частицы (т.е. скорости частицы относительно потока), для значений Re > 1 - пропорционально степени, большей единицы. Если рассматривают процесс седиментации высокодисперсных частиц, то условие Re < 1 обычно выполняется, и поэтому, в принятых по характеру кинематики потока допущениях, силу сопротивления движению частицы рассчитывают в соответствии с формулой Стокса
Fc = -3pmdv, (6.12)
где Dr, m и d имеют тот же смысл, что и ранее, по тексту, v = vr - радиальная скорость частицы.
Тогда, подставляя (6.12) в (6.11), получают
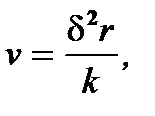(6.13)
где
k =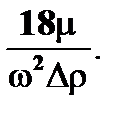 
(6.14)
Исходя из дифференциального уравнения движения частицы, вследствие (6.13) имеют
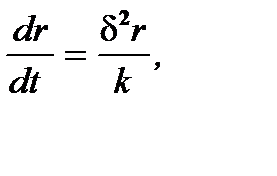
откуда, разделяя переменные
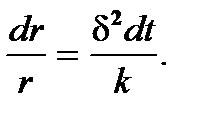(6.15)
Интегрируя (6.15) слева по r в пределах от r до R, справа по t от 0 до t, находят частное решение уравнения (6.15)
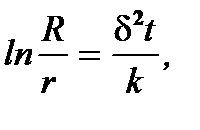(6.16)
откуда получают выражение текущего критического диаметра частицы как функции координаты r и времени t
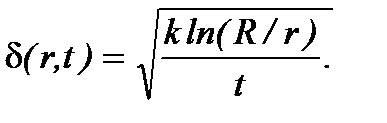(6.16)
Физический смысл определяемой по (6.16) величины заключается в том, что при одинаковых условиях по начальным данным, частица диаметром d¢ > d достигнет стенку ротора быстрее, чем частица диаметром d.
Проводя проверку на асимптотику формулы (6.16), при limr®Rdк = 0, limt®¥dк = 0, limt®0dк = ¥, убеждаются в согласии величины текущего критического диаметра частицы dк физическому смыслу исследуемого явления.
Из формулы (6.16) вытекает выражение для критического диаметра осадительной центрифуги в виде функции от времени t и физико-механических и геометрических параметров анализируемого процесса
dк =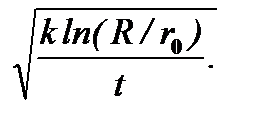 
(6.17)
В свою очередь, из формулы (6.17) следует зависимость времени Т осаждения частицы от значения dкр
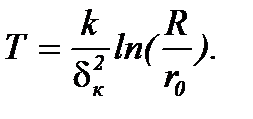(6.18)
Для того чтобы получить интегральную характеристику по количеству оседающих на стенке ротора частиц из цилиндрического объема r0 £ r £ R и единичной высоты, выделяют элементарную трубку радиусами r, r + dr и той же высоты (рис. 6.4).
Причем, из выделенного объема (r, r + dr) суспензии за время t осаждается количество частиц, равное
dn1 = (2prdr)n0Ф[d(r,t)], (6.19)
где Ф(d) = 1 - F(d), F(d),Ф(d) - соответственно, счетная и характеристическая функции распределения частиц по крупности.
Интегрируя (4.11) слева по числу n оседающих частиц, а справа - по r - по толщине потока, имеют
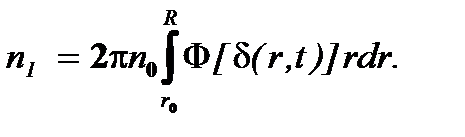(6.20)
| r0 |
| r |
| dr |
| R |
| o |
Рис. 6.4
С другой стороны, так как тот же объем суспензии включает p(R2 - r02)n0 частиц, то в качестве счетного коэффициента осветления, в силу (6.20), получают
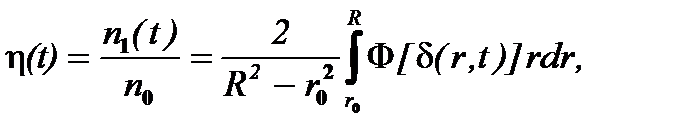(6.21)
а в качестве счетного коэффициента уноса
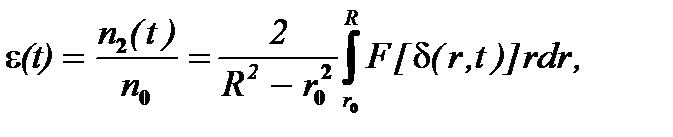(6.22)
где n2(t) - количество частиц в осветленной суспензии (фугате) в том же объеме ротора.
Принимая во внимание формулу (6.20), например, для коэффициента уноса e получают в явной форме
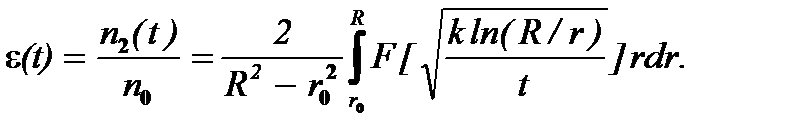(6.23)
Учитывая, что, по определению, F(0) = 0, F(¥) = 1, проверкой на асимптотическое поведение по времени коэффициента уноса (6.23)
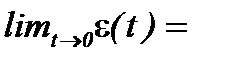
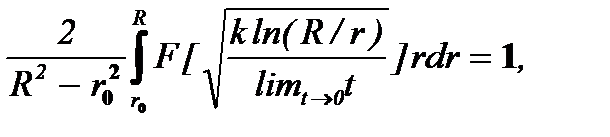
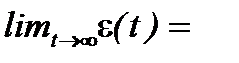
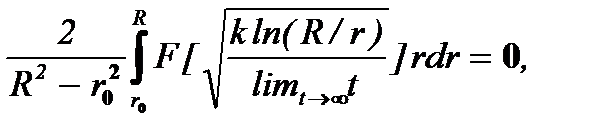
убеждаются в согласии с физическим смыслом данного коэффициента.
Кроме того, поскольку F¢(d) > 0, R > r, то в соответствии с (6.23) частная производная по времени коэффициента уноса
=
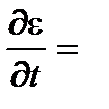
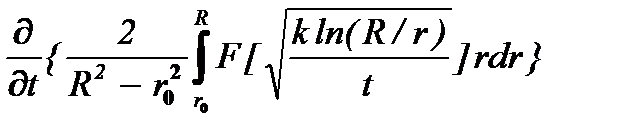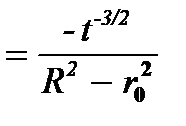
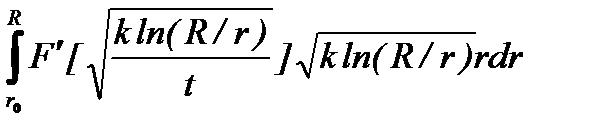< 0,
то, как и должно быть, коэффициент уноса быстро убывает с течением времени (суспензия осветляется с ростом времени), с порядком убывания О(t-3/2).
Соответственно, при тех же условиях, коэффициент осветления h(t) - возрастающая функция t .
Принимая во внимание формулу (6.18), выражению (6.23) придают удобный для расчетов вид
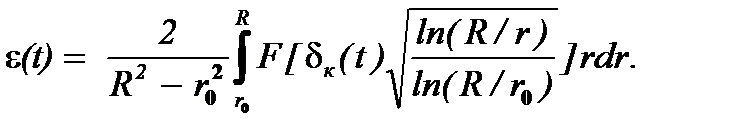(6.24)
Формулы (6.21) - (6.24) полагают в основу количественного анализа процесса осаждения высокодисперсных частиц в роторе центрифуги периодического действия.
Дата: 2019-02-02, просмотров: 207.
