Уравнения Эйлера динамики  идеальной жидкости

Уравнения движения Л. Эйлера устанавливают связь между дав­лением и скоростью движения идеальной жидкости в любой точке потока.

Если к действующим на выделенный объем dV массовой силе F(X,Y,Z) и силе давления gradр(¶р/¶х, ¶р/¶у, ¶р/¶z) добавить силу инерции dФ = - d т(dv/d t) = -rd х d у dz(dv/d t), то согласно принципу Даламбера, исходя из уравнений равновесия (2.2), приходят к системе уравнений динамики идеальной жидкости

dv_x/dt = X - (1/r)(¶р/¶х),

dv_y/dt = Y - (1/r)(¶р/¶y),                                                           (3.1)

dv_zdt = Z - (1/r)(¶р/¶z).

Входящие в левые части (3.5) составляющие ускорение имеют вид 

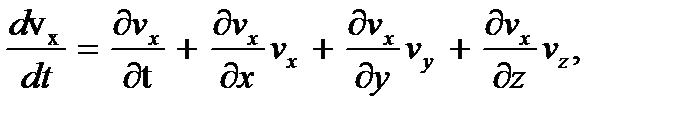
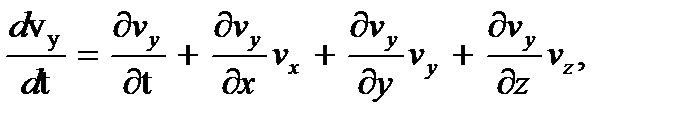                                               (3.2)

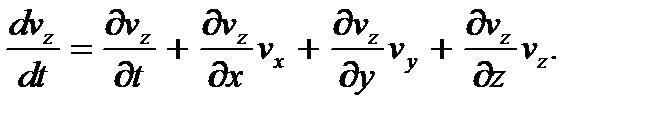
В этой системе уравнений производные (dv_x/dt ) , (dv_y/dt ) и (dv_z/dt ) характеризуют составляющие ускорения вдоль соответствующих осей.

Система уравнений (4.2) является системой дифференциальных уравнений движения идеальной жидкости (Л. Эйлер, 1755 г.).

Уравнение Бернулли и его приложения в технике

С целью получить интеграл уравнений (3.1), предварительно, преобразуют формул (3.2). Для чего,  имея в виду зависимости

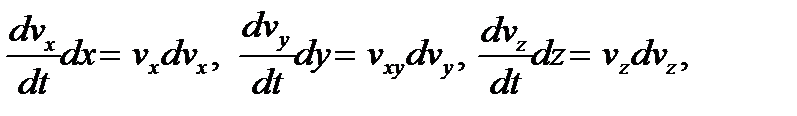
умножают каждое из (3.2) выражений, последовательно, на dx, dy, dz и суммируя полученные результаты,  приходят к соотношению

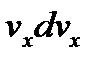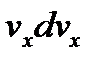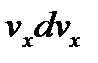    + +  = Xdx + Ydy + Zdz -  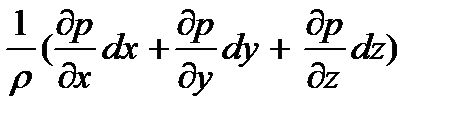 (3.3)

   Поскольку согласно свойству дифференциала

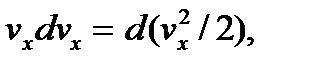
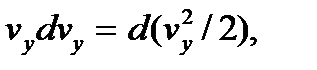
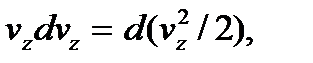
то левую часть  преобразуют к виду

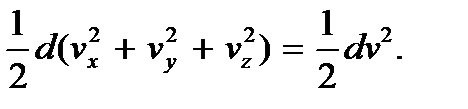                                                                                                                     (3.4)

    Если в правой части уравнения (3.3) принять Xdx + Ydy + Zdz = dU и

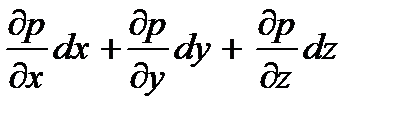= dр, то с учетом (3.4) данное дифференциальное уравнение принимает форму

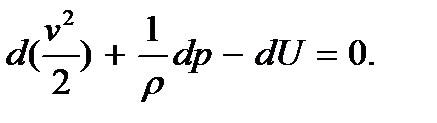                                                                     (3.5)

           В том случае, когда в качестве массовой силы выступает силы тяжести и поэтому dU = -gdz, то на основе (3.5) приходят к соотношению

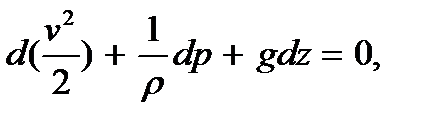
откуда  для  несжимаемой жидкости, при r = const, получают

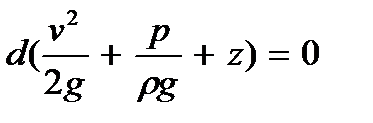
и тогда, интегрируя

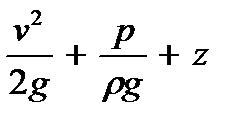    = const.                                                                   (3.6)

    Интеграл дифференциального уравнения (3.3) в форме (3.6) носит название уравнения  (закона) Бернулли.

    Так, если на некоторой высоте z₁ потока жидкости скорость жидкости v₁, давление р₁, то согласно (3.6) на высоте z₂ скорость жидкости v₂ и давление р₂ удовлетворяют соотношению

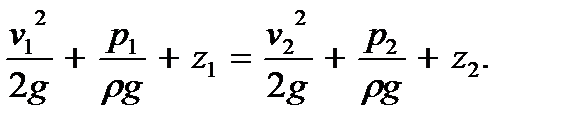                                                                                                    (3.7)

           Выражение (3.6) по своему физическому смыслу является отнесенным к единице веса жидкости  значением  полной энергии субстанции этого веса. Причем v²/2g, p/(rg), соответственно, так называемый, скоростной и пьезометрический напор, 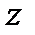- нивелирная или геометрическая  высота.

Уравнение (3.7) как явное выражение закона Бернулли, было получено в близкой к (3.6) форме в 1738 г. Даниилом Бернулли, и оно сыграло и продолжает играть исключительно важную роль в  самых разнообразных технических вопросах динамики жидкости и газа.  Например, в самолетостроении, при проектировании гидротехнических сооружений, гидротурбин, гидроавтома­тики, гидроприводов, трубопроводов, насосов и др.

    Лекция 4.  Основы теории динамики вязкой несжимаемой жидкости.

Дифференциальные уравнения движения вязкой несжимаемой жидкости (уравнения Навье-Стокса).