Расчетным случаем ТМ является транспортирование изделий с учетом коэффициента динамичности Кд.
Расчет производится следующих элементов ТМ: рамы, колесной оси, откидной опоры, подвески и т.д.
Рассмотрим проектирование рамы ТМ, которое включает расчеты на прочность и жесткость.
Целью расчета рамы ТМ на прочность является выявление максимальных нагрузок и напряжений в ее ответственных сечениях и сравнение их с допустимыми.
На раму ТМ действуют (рис. 128) нагрузки от веса изделий РА и РВ, реакции колесного хода R с и R к, собственный вес рамы Gрам и закрепленного на ней оборудования Pi .
Нагрузки РА, РВ, Rc , R к находятся при развеске ТМ.
Расчеты нагрузок от веса рамы существенно упрощаются при постоянной интенсивности qx распределении ее веса по длине 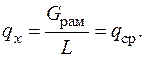
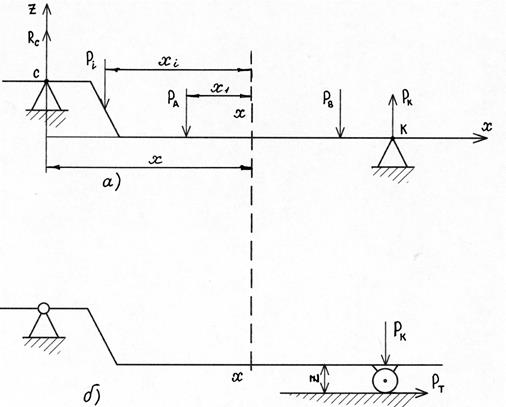
Рис. 128. К расчету рамы TМ на прочность
Найдем статический изгибающий момент в сечении рамы x - x от действия всех сил (рис .128).
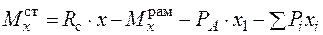 ,
,
где Р i - сосредоточенный вес i -го элемента оборудования;
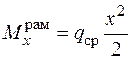 - изгибающий момент от веса рамы.
- изгибающий момент от веса рамы.
Динамический изгибающий момент будет равен

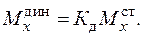
При торможении ТМ на ее раму действует дополнительный изгибающий момент МТ от силы торможения РТ.
МТx = PТ × z ,
где z – расстояние от поверхности грунта до центра балки рам.
РТ = j R к ,
где j – коэффициент сцепления, j =0,6–0,8.
Таким образом, за расчетный изгибающий момент Mpmax действующий в сечении x - x рамы, можно принять максимальный из моментов
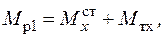
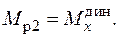
Напряжение в искомом сечении рамы ТМ будет равно
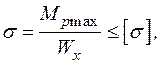
где Wx – момент сопротивления сечения при изгибе.
Подбором размеров и формы сечений рамы (параметра Wx) добиваются выполнения данного условия.
При расчете на жесткость раму рассматривают как балку на двух опорах С и К , на которую действуют силы РА, РВ и равномерно распределенная нагрузка q с р от собственного веса рамы со всем оборудованием на ней (рис. 129).
В практических расчетах принимают для двухопорных балок при нагрузках, направленных в одну сторону, в качестве максимального прогиба - прогиб посередине пролета. Это существенно упрощает расчеты.
Используя принцип независимости действия сил, найдем прогиб z рамы как сумму прогибов от действия каждой из сил
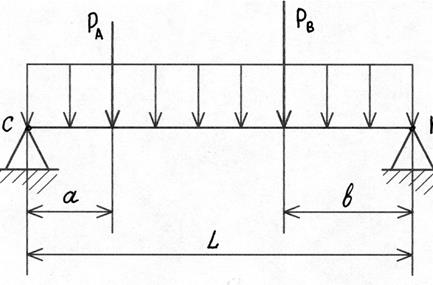 |
Рис. 129. К расчету рамы ТМ на жесткость
z = zq + zA + zB .
Прогиб от распределенной нагрузки qср, равен [45]
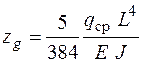
Прогиб от силы P А
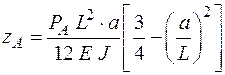 .
.
Прогиб от силы P В
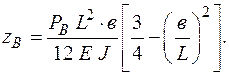
Найденный прогиб не должен превышать допускаемую величину
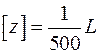 ,
, 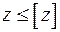 .
.
Данные аналитические расчеты рамы ТМ носят приближенный характер, так как не в полной мере учитывают ее конструктивно-силовую схему, связи элементов, переменный профиль сечений, точные места приложения нагрузок и др.
Более точных результатов и снижения весовых характеристик можно достигнуть при расчете конструкции рамы ТМ методом конечных элементов (КЭ).
Дата: 2019-02-02, просмотров: 612.