Принципиальная схема механизма изменения вылета стрелы с жесткой кинематической связью со стрелой может быть представлена в виде гидравлического домкрата расположенного между стрелой и поворотной рамой крановой установки и шарнирно связанного с ними.

При проведении расчетов будем считать, что известны нагрузки на стрелу: вес груза Q × g; сила инерции при торможении груза P_ин ; вес стрелы G_c центробежная сила Р_ц , возникающая во время поворота крановой установки, действующая в плоскости стрелы в горизонтальном направлении; сила ветра Р_в1, действующая на груз и приложенная к головке стрелы в горизонтальном направлении, а также плечи действия этих сил l_c, l и положение точек О, О₁, О₂ крепления стрелы, верхнего и нижнего шарниров домкрата (параметры a, h₁, h₂).

Рациональные значения параметров a, h₁, h₂ могут быть найдены одним из методов оптимизации на основе кинематического и силового расчетов механизма.

На рис. 138 приняты следующие обозначения:

(·) О - ось вращения стрелы;

О₁О₂= l₀  - длина домкрата при крайнем положении стрелы;

      a - текущий угол подъема стрелы;

О₁ОО₂=a₁-угол, фиксирующий исходное положение верхнего шарнира домкрата относительно нижнего;

a₂ - угол возвышения стрелы относительно горизонта, при ее крайнем нижнем положении;

ОО₁=а; ОО₂= b .

Так как грузоподъемность крана Q зависит от вылета стрелы (угла a), то расчеты необходимо приводить для нескольких положений стрелы (при углах a₂£ a £ a_max).

В ходе кинематического расчета определяются длины домкрата l_Н, l_B при крайних нижнем и верхнем положениях стрелы, ход штока домкрата D l, линейная скорость и перемещения штока при заданном времени t подъема стрелы по выражениям

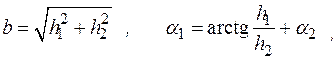
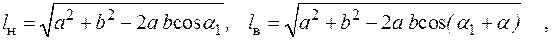
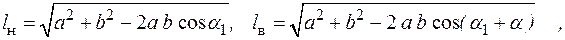
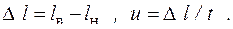
Изменение вылета стрелы будет происходить при выполнении условия

,

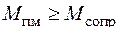
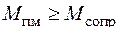где М_пм   - момент силы, развиваемой механизмом;

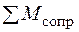- суммарный момент сил сопротивления подъему.

,

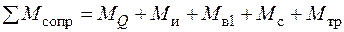где 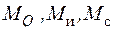- момент от веса груза, силы инерции и веса стрелы соответственно;

М_в1 , М_тр - моменты от силы ветра на груз и сил трения в шарнирных соединениях соответственно.

Данные моменты находятся из следующих выражения:

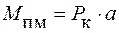;                                    (152)

,

,

,

.

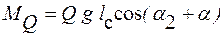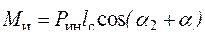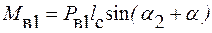Силу Р_к можно представить следующим образом:

,

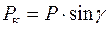тогда

.

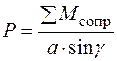Из 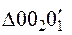найдем sing по теореме синусов

,

тогда

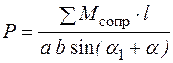 .                        (153)

Нагрузка на цапфы стрелы P_Н   будет равна

,

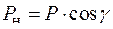Проведя данные расчеты для нескольких положений стрелы (углов a), можно найти максимальную нагрузку на гидроцилиндр P_max .

По найденным нагрузкам P_max, P_Н можно произвести расчеты гидроцилиндра и стрелы.

Для положения стрелы, при котором P = P_max, можно найти рациональные значения параметров компоновки механизма а, h₁, h₂ (положение точек О,О₁,О₂), при которых  потребное усилие гидроцилиндра будет минимальным.

Математически это можно представить следующим образом

;                                                          

;

;

.

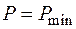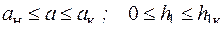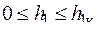Здесь 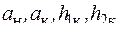ограничения на соответствующие параметры.

Данная задача может быть решена методом простого перебора по трем параметрам 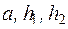 или по двум параметрам  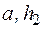(при фиксированном значении 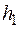) с расчетом величины Р .

Разработанная математическая модель функционирования механизма изменения вылета стрелы с жесткой подвеской позволяет разработать программу для ЭВМ по выбору рациональных его параметров.