Все коэффициенты канонических и свободные члены канонических уравнений метода перемещений являются реактивными усилиями, возникающими в дополнительно введенных связях основной системы, от загружения её одним углом поворота, численно равным 1 (единице), одним линейным смещением, численно равным 1 (единице), или всеми заданными внешними силами одновременно.
Первый индекс коэффициента или свободного члена канонических уравнений соответствует порядковому номеру дополнительно введенной связи основной системы. Второй индекс соответствует номеру единичного перемещения (угла поворота или линейного перемещения) или всех внешних нагрузок, приложенных к основной системе. Физический смысл каждого коэффициента и свободного члена канонических уравнений совпадает с физическим смыслом этих уравнений. В плавающих заделках основной системы возникают реактивные моменты, а в шарнирно стержневых связях возникают сосредоточенные силы.
Например, коэффициент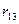 
- есть реактивное усилие, возникающее в дополнительно введенной связи 1 основной системы, загруженной кинематическим воздействием 
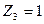(углом поворота узла 3 или его линейным смещением).
Свободные члены канонических уравнений являются реактивными усилиями в дополнительно введенных связях основной системы, загруженной заданными внешними нагрузками.
Например,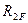 
- есть грузовое реактивное усилие в дополнительно введенной связи 2 основной системы, загруженной внешними заданными нагрузками.
Все коэффициенты канонических уравнений метода перемещений (как и в методе сил) разделяют на главные и побочные. Главные коэффициенты имеют одинаковые индексы, располагаются по главной диагонали системы канонических уравнений и всегда имеют положительные значения. Побочные коэффициенты имеют разные индексы и могут иметь положительные, отрицательные или нулевые значения. Побочные коэффициенты, расположенные симметрично главной диагонали имеют одинаковые численные значения, т.е. обладают свойством взаимности (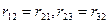 
и т.д.).
8.6 Построение единичных и грузовой эпюр изгибающих моментов в основной системе метода перемещений.
Для построения единичных эпюр изгибающих моментов в основной системе метода перемещений используют эпюры, построенные для отдельных стержней с двумя защемленными опорами, либо одной защемленной, а другой шарнирной опорами, загруженных единичными поворотами одной защемленной опоры, либо единичным линейным перемещением одной из опор, направленным перпендикулярно оси стержня. Опорные моменты и реакции опор указанных стержней легко определяются по методу сил. При этом опорные моменты и реакции опор удобно выражать через погонные жесткости стержней, равные отношению абсолютной изгибной жесткости стержня к его длине, т.е.:
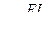(8.7)
Для построения грузовой эпюры изгибающих моментов в основной системе необходимо знать длины стержней, виды их опор и характер внешних нагрузок, действующих на каждый стержень.
Опуская выводы, приводим основные эпюры изгибающих моментов для указанных выше двух типов стержней, которые используются при построении единичных и грузовых эпюр в основной системе метода перемещений:
1. Стержень с двумя защемленными опорами, имеющий длину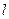 
и погонную жесткость 
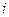загружен единичным поворотом одной из опор.
На рис.8.12 приведена эпюра изгибающих моментов от поворота опоры (А) по часовой стрелке на единичный угол, а также показаны направления и величины опорных реакций стержня.
Анализируя эту эпюру, можно сформулировать следующие её свойства:
а) изгибающий момент в опорном сечении А стержня равен учетверенной погонной жесткости этого стержня и растягивает нижние волокна стержня;
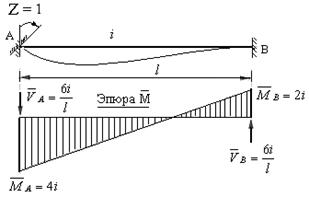
Рис.8.12
б) изгибающий момент в опорном сечении (В) стержня равен удвоенной погонной жесткости стержня и растягивает верхние волокна стержня;
в) опорные реакции стержня равны отношению ушестеренной погонной жесткости к длине стержня и вращают стержень против заданного единичного поворота опоры.
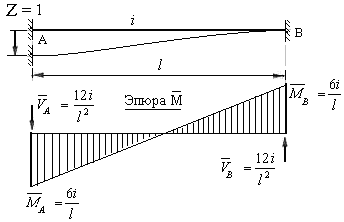
Рис.8.13
2. Стержень с двумя защемленными опорами, имеющий длину 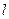и погонную жесткость 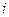загружен единичным линейным смещением одной из опор, направленным перпендикулярно оси стержня (рис.8.13).
Из анализа эпюры изгибающих моментов следует, что изгибающие моменты в опорных сечениях стержня имеют одинаковые модули, но противоположны по знаку. При этом ордината эпюры изгибающих моментов у опоры, которая получает линейное смещение, всегда откладывается от нулевой прямой в сторону заданного смещения, а ордината эпюры под другой опорой откладывается в противоположную сторону. Величины реакций опор определяются отношением суммы опорных моментов к длине пролета стержня и направляются так, чтобы они вращали стержень в том же направлении, в котором стремится его повернуть единичное смещение.
3. Стержень с одной защемленной, а другой шарнирной опорами, имеющий длину 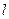и погонную жесткость 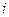загружен единичным поворотом защемленной опоры (рис.8.14)
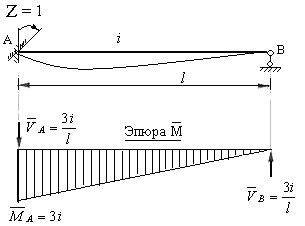
Рис.8.14
Свойства построенной эпюры изгибающих моментов легко устанавливаются по аналогии с предыдущими эпюрами.
4. Стержень с одной защемленной, а другой шарнирной опорами, имеющий длину 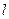и погонную жесткость 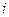загружен единичным линейным смещением одной из опор в направлении, перпендикулярном оси стержня (рис.8.15).
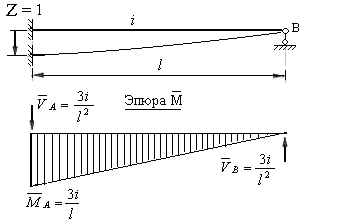
Рис.8.15
Свойства построенной эпюры изгибающих моментов устанавливаются по аналогии с предыдущими эпюрами.
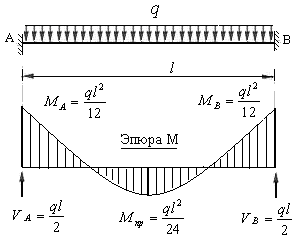
Рис.18.16
5. Стержень с двумя защемленными опорами, имеющий длину 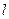загружен равномерно распределенной нагрузкой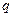 
Эпюра изгибающих моментов в рассматриваемом случае очерчена по квадратичной параболе, имеющей вершину посередине пролета стержня. Опорные и максимальный пролетный изгибающие моменты определяются по формулам, приведенным на эпюре изгибающих моментов. Реакции опор стержня имеют величины, равные половине всей нагрузки и направлены вверх.
6. Стержень с двумя защемленными опорами длиною пролета 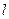загружен сосредоточенной силой 
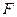в любом месте пролета (рис.8.17).
При таком загружении стержня эпюра изгибающих моментов ограничена на каждом участке прямыми линиями, наклонными к оси стержня. Опорные моменты и пролетный момент под силой определяются по формулам, приведенным на эпюре изгибающих моментов. Реакции опор стержня направлены вверх (противоположно направлению внешней нагрузки) и определяются по формуле Журавского.
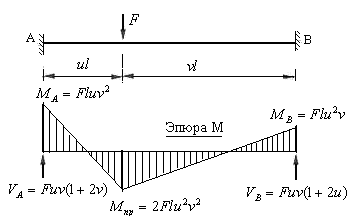
Рис.8.17
В частном случае, когда сила 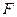приложена посередине пролета стержня ( 
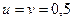) опорные изгибающие моменты, а также изгибающий момент под точкой приложения силы, численно равны и определяются по формуле: 
.
Реакции опор направлены вверх и равны половине заданной силы:
7. Стержень с одной защемленной, а другой шарнирной опорами, длина пролета, которого равна 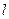, загружен равномерно распределенной нагрузкой (рис.8.18).
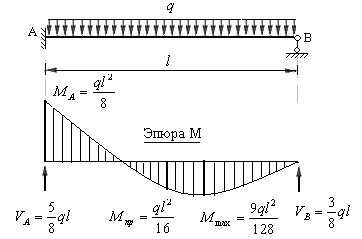
Рис.8.18
На рис.8.18 приведена эпюра изгибающих моментов, построенная на растянутых волокнах стержня, реакции опор стержня (их истинные направления и величины), а также значения опорного, пролетного и максимального изгибающих моментов.
Следует иметь в виду, что сечение стержня, в котором возникает максимальный изгибающий момент, находится на расстоянии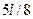 
от защемленной опоры, или на расстоянии 
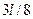от шарнирной опоры.
8. Стержень длиною 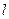с одной защемленной, а другой шарнирной опорами, загружен сосредоточенной силой в произвольной точке пролета (рис.8.19).
Эпюра изгибающих моментов и величины ординат показаны на рис.8.19.
В частном случае, когда сила 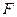приложена посередине пролета стержня (в этом случае 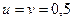) опорный изгибающий момент и пролетный изгибающий момент будут соответственно равны:
, 
.
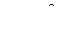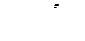Реакции опор легко вычисляются по формуле Журавского и соответственно равны:
, 
.
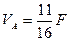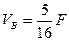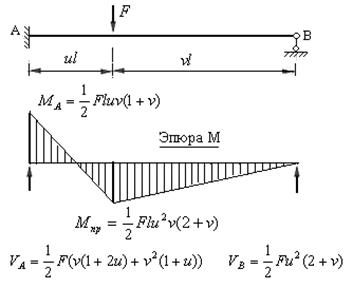
Рис.8.19
9. Стержень длиною 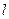с двумя защемленными опорами загружен в произвольном месте сосредоточенным моментом 
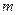(рис.8.20).
На рис.8.20 приведена эпюра изгибающих моментов, величины изгибающих моментов на концах участков и величины реакции опор, возникающие от сосредоточенного момента, направленного по ходу часовой стрелки, т.е. имеющего знак плюс.
Если внешний сосредоточенный момент действует против часовой стрелки, то его следует подставить в приведенные формулы со знаком минус.
В частном случае, когда внешний момент 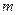приложен посередине пролета стержня (в этом случае 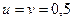) опорные изгибающие моменты, изгибающие моменты в сечении, где приложен внешний момент, а также величины реакций опор, будут соответственно равны: 
, 
,
, 
, 
.
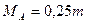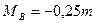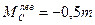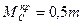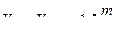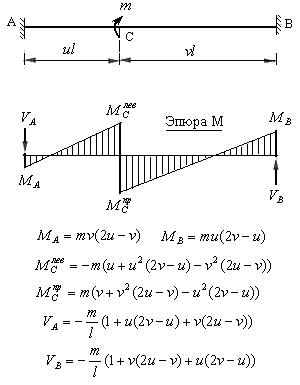
Рис.8.20
10. Стержень длиною 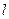с одной защемленной, а другой шарнирной опорами, загружен сосредоточенным моментом 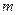в произвольной точке (С) пролета (рис.8.21).
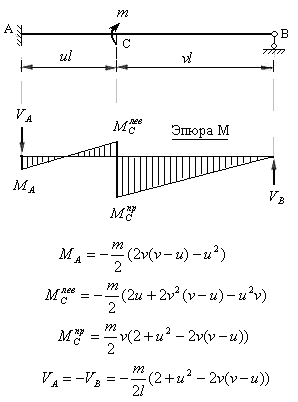
Рис.8.21
На рис.8.21 приведена эпюра изгибающих моментов, величины изгибающих моментов на концах участков и величины реакции опор, возникающие от сосредоточенного момента, направленного по ходу часовой стрелки, т.е. имеющего знак плюс.
В частном случае, когда внешний момент 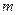приложен посередине пролета стержня (в этом случае 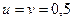) опорный изгибающий момент, изгибающие моменты в сечении, где приложен внешний момент, а также величины реакций опор, будут соответственно равны: 
,
, 
, 
, 
.
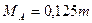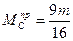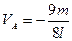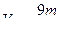Для построения единичных эпюр изгибающих моментов в основной системе метода перемещений, необходимо вычислить погонные жесткости всех стержней заданной рамы и привести их к одной минимальной погонной жесткости 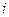. Погонные жесткости каждого стержня определяются делением их абсолютных жесткостей на длины. Путем сравнения полученных величин определяется минимальная погонная жесткость, которая обозначается 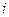. Жесткости других стержней будут иметь значения, равные произведению некоторых постоянных коэффициентов и величины .
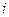Используя приведенные выше эпюры изгибающих моментов для отдельного стержня (п.1-4), легко построить единичные эпюры изгибающих моментов в основной системе метода перемещений для любой рамы.
Используя эпюры изгибающих моментов для отдельных стержней (п. 5 – 10), легко построить грузовую эпюру в основной системе метода перемещений для любой заданной рамы.
Жесткие узлы рамы в основной системе метода перемещений никогда не находятся в равновесии под действием узловых изгибающих моментов, вычисленных при построении единичных и грузовой эпюр.
В этом состоит одно из коренных отличий расчета статически неопределимых рам методом перемещений и методом сил.
Ниже, при решении конкретных примеров расчета статически неопределимых рам методом перемещений, будут даны подробные разъяснения и рекомендации, которые следует использовать при построении единичных и грузовой эпюр изгибающих моментов в основной системе.
8.7 Определение коэффициентов и грузовых реакций
канонических уравнений.
Коэффициенты и грузовые реакции канонических уравнений могут быть определены двумя способами:
- статическим способом, основанным на использовании условий равновесия узлов или дисков;
- способом перемножения эпюр изгибающих моментов по правилу Верещагина.
При использовании первого способа следует установить физический смысл определяемого коэффициента или свободного члена канонических уравнений.
Если он является реактивным моментам, возникающим в плавающей заделке основной системы, то для его определения следует вырезать (из единичной или грузовой эпюры изгибающих моментов) узел, содержащий эту заделку. Вырезанный узел необходимо загрузить неизвестным реактивным моментом, направленным по часовой стрелке и известными узловыми изгибающими моментами в рассеченных стержнях. Величины и направления этих моментов легко устанавливаются по эпюре, которая соответствует второму индексу определяемого реактивного момента.
Сумма моментов, действующих на вырезанный узел должна быть равной нулю. Из этого условия составляется уравнение равновесия узла и вычисляется неизвестный коэффициент или свободный член канонических уравнений.
Если определяемый коэффициент или свободный член канонических уравнений является реактивной сосредоточенной силой в дополнительно введенной шарнирно стержневой связи основной системы, то для его определения следует вырезать замкнутым сечением из единичной или грузовой эпюры диск, содержащий шарнирно стержневую связь.
Вырезанный диск необходимо загрузить неизвестной реактивной сосредоточенной силой, возникающей в соответствующей связи основной системы (эта сила направляется в сторону заданного линейного смещения), а также поперечными силами в рассеченных стержнях основной системы.
Величины и направления поперечных сил легко устанавливаются по соответствующей единичной или грузовой эпюре изгибающих моментов. Величины и знаки поперечных сил определяются по формуле Журавского, как тангенс угла наклона эпюры М к оси стержня.
Поперечная сила, имеющая положительный знак направляется так, чтобы она вращала вырезанный диск по часовой стрелке.
Поперечная сила, имеющая отрицательный знак направляется так, чтобы она вращала вырезанный диск против часовой стрелки.
Сумма проекций всех сил, действующих на вырезанный диск, на направление шарнирно стержневой связи должна быть равна нулю. Из этого условия составляется уравнение равновесия диска и определяется искомый коэффициент или свободный член канонического уравнения.
При использовании второго способа коэффициенты канонических уравнений определяются перемножением единичных эпюр изгибающих моментов по правилу Верещагина. При этом абсолютные жесткости стержней определяются умножением погонных жесткостей на их длины.
Для определения грузовых реакций необходимо построить дополнительно грузовую эпюру изгибающих моментов в основной системе метода сил. При этом рекомендуется принимать любой вариант основной системы.
Результат перемножения грузовой эпюры изгибающих моментов в основной системе метода сил на единичную эпюру изгибающих моментов в основной системе метода перемещений равняется искомой грузовой реакции, взятой с противоположным знаком.
Этот способ более сложный, чем статический и применяется лишь при расчете рам с наклонными стойками, когда статическим способом не удается определить некоторые из коэффициентов и грузовых реакций. Ниже, при решении конкретных примеров, будут приведены дополнительные пояснения по использованию этого способа.
Дата: 2019-02-02, просмотров: 370.
