Неподвижность ферм на плоскости обеспечивается при помощи шарнирных опор. В балочных и однопролетных балочно-консольных фермах устанавливают одну шарнирно неподвижную и одну шарнирно подвижную опоры. В многопролетных балочно-консольных фермах дополнительно устанавливают шарнирно подвижные опоры из расчета одна опора на каждый дополнительный пролет фермы.
В арочных фермах устанавливают две шарнирно неподвижные опоры.
В соответствии с этим реакции опор балочных и
балочно-консольных ферм определяют по методу равновесия дисков или по методу неполного освобождения связей, как и реакции опор соответствующих балок.
Если однопролетная балочная ферма загружена силами, расположенными симметрично опор, то их равны половине суммы всех сил.
Реакции опор арочных ферм (вертикальные составляющие реакций и распор) определятся как для трехшарнирной арки.
5.4 Аналитические методы определения усилий в стержнях ферм.
При загружении ферм узловыми сосредоточенными силами, в их стержнях возникают продольные усилия растяжения или сжатия. Для того, чтобы выявить усилие необходимо рассечь стержень, или полностью удалить его. Тогда к двум узлам, которые объединяет рассеченный или удаленный стержень, необходимо приложить равные и противоположно направленные усилия вдоль оси стержня. Если стержень растянут, то усилия направляют от узлов, если же стержень сжат, то усилия следует направить к узлам. Если усилия неизвестны, то их следует направить от узлов, т.е. в соответствии с растяжением. Растягивающие усилия имеют знак плюс, а сжимающие усилия имеют знак минус.
Для определения усилий в стержнях простых плоских ферм используют два метода:
1) метод равновесия узлов;
2) метод равновесия дисков.
Рассмотрим последовательно эти методы, раскроим их сущность и возможности использования для определения усилий в стержнях ферм.
Метод равновесия узлов состоит в том, что для определения усилий в стержнях заданной фермы освобождают (удаляют) все стержни и все опоры этой фермы. В результате получают ряд изолированных узлов. Каждый узел загружают заданными внешними силами, реакциями опор и неизвестными усилиями в удаленных стержнях. При этом величины и направления реакций опор рекомендуется определить предварительно из условий равновесия фермы в целом (в соответствии с пояснениями, приведенными в § 5.3). Для каждого узла составляются два уравнения равновесия, используя условия:
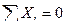 и
и 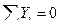 . (5.1)
. (5.1)
Всего для фермы можно составить 2У уравнений равновесия. Где У, число шарнирных узлов фермы.
Для того, чтобы получить уравнения с разделенными неизвестными, необходимо установить рациональный порядок составления уравнений и выбрать рациональные направления осей проекций.
Сначала необходимо составить уравнения равновесия для узлов фермы, которые объединяют два стерня, затем для узлов, объединяющих три стержня и т. д. Оси проекций следует направлять перпендикулярно к линиям действия неизвестных усилий.
Рассмотрим, к примеру, двухпанельную ферму с параллельными поясами и раскосной решеткой, загруженную силами в узлах, как показано на рис.5.11. Вычислим предварительно реакции опор фермы:
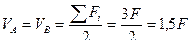
Освободим (удалим) все стержни и опоры фермы, в результате получим 6 отдельно расположенных узлов
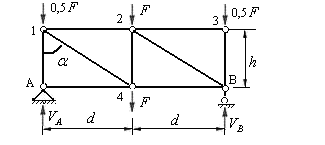
Рис.5.11
(рис.5.12). Опорные узлы загружаем вычисленными реакциями опор, а остальные узлы заданными внешними силами.
Дополнительно каждый узел загружаем неизвестными усилиями, направленными от узлов (рис.5.12). Эти усилия обозначаем буквой 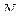 с двумя индексами, соответствующими обозначениям двух узлов, которые объединяются стержнем.
с двумя индексами, соответствующими обозначениям двух узлов, которые объединяются стержнем.
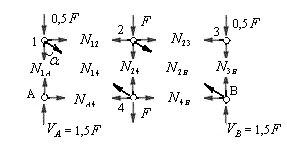
Рис.5.12
Для каждого узла фермы можно составить два уравнения равновесия. Всего для 6 узлов фермы – 12 уравнений. Из них необходимо определить 9 неизвестных усилий в стержнях. Три условия равновесия фермы в целом уже использованы при определении реакций опор.
Составляем уравнения равновесия узла А, на который действуют два неизвестных усилия и реакция опоры. Оси проекций направляем перпендикулярно неизвестным усилиям, т. е ось 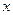 горизонтально вправо, а ось
горизонтально вправо, а ось 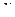 вертикально вверх. Используя условия (5.1), получим:
вертикально вверх. Используя условия (5.1), получим:
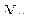 = 0, и
= 0, и 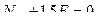


Таким образом, усилие в стержне А4 равно нулю, а усилие в стержне 1А имеет знак минус, следовательно, он сжат.
Составляем уравнения равновесия узла 3, на который действуют два неизвестных усилия и заданная сила равная 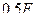 . Оси проекций направляем перпендикулярно неизвестным усилиям, т. е ось
. Оси проекций направляем перпендикулярно неизвестным усилиям, т. е ось 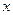 горизонтально вправо, а ось
горизонтально вправо, а ось 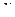 вертикально вверх. Используя условия (5.1), получим:
вертикально вверх. Используя условия (5.1), получим:
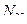 = 0, и
= 0, и 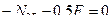

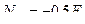
Таким образом, усилие в стержне 23 равно нулю, а усилие в стержне 3В имеет знак минус, следовательно, этот стержень сжат.
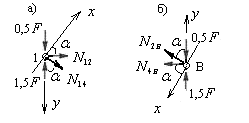
Рис.5.13
Рассматриваем равновесие узла 1, объединяющего 3 стержня (рис.5.13,а). Загружаем этот узел неизвестными усилиями в стержнях 1-2 и 1-4, а также вычисленным ранее усилием в стержне 1А. Так как стержень 1А сжат, то усилие равное - 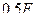 следует направить к узлу 1 и указать его модуль.
следует направить к узлу 1 и указать его модуль.
Выбираем рациональные направления осей проекций. Ось 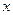 направляем перпендикулярно неизвестному усилию в раскосе 1-4, а ось
направляем перпендикулярно неизвестному усилию в раскосе 1-4, а ось 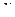 направляем перпендикулярно неизвестному усилию в стержне 1-2 верхнего пояса фермы.
направляем перпендикулярно неизвестному усилию в стержне 1-2 верхнего пояса фермы.
Составляем уравнения равновесия узла 1, используя условия: 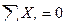

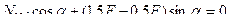
Из полученного уравнения находим: 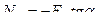 , где
, где 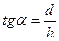 . Стержень верхнего пояса фермы сжат, а его величина (модуль) зависит от соотношения длины панели к высоте фермы, или от угла наклона раскоса к вертикали (угла
. Стержень верхнего пояса фермы сжат, а его величина (модуль) зависит от соотношения длины панели к высоте фермы, или от угла наклона раскоса к вертикали (угла 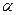 ).
).
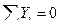

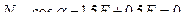

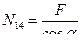 .
.
Раскос 1-4 фермы 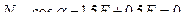 растянут , и его величина также зависит от угла
растянут , и его величина также зависит от угла 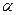 . Напомним, что нисходящие раскосы ферм всегда растянуты.
. Напомним, что нисходящие раскосы ферм всегда растянуты.
Составляем уравнения равновесия узла В заданной фермы. Узел загружен силами, показанными на рис. 5.13,б.
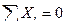

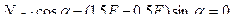

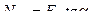
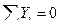

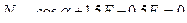

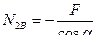
Таким образом, стержень 4-В нижнего пояса фермы растянут, а восходящий раскос 2-В сжат.
Неизвестное усилие в стойке 2-4 определяем из равновесия узла 4 (или из равновесия узла 2). На рис.5.14 показаны силы, действующие на узел 4. Составим уравнение равновесия из условия 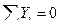

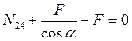

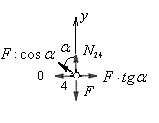
Рис.5.14
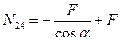
Усилие в стойке 2-4 имеет знак минус, следовательно, стойка 2-4 сжата.
Составим уравнение равновесия узла 4, используя условие:
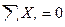

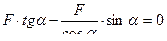

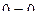 .
.
Полученное тождество свидетельствует о том, что усилия в стержнях фермы вычислены правильно. Узел 2 рассматриваемой фермы объединяет 4 стержня, усилия в которых уже найдены из условий равновесия соседних узлов. Если составить уравнения равновесия этого узла, то они обратятся в тождества 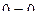 , что также будет являться подтверждением правильности определения усилий.
, что также будет являться подтверждением правильности определения усилий.
Многие плоские фермы имеют однотипные узлы, объединяющие два или три стержня, усилия в которых можно определить без составления уравнений равновесия. Рассмотрим четыре случая:
1) Узел объединяет два стержня и не загружен. (рис.5.15,а). Усилия в обоих стержнях равны нулю.
2) Узел объединяет два стержня и загружен силой  , линия действия которой совпадает с осью одного из стержней (рис.5.15,а). В этом случае усилие в загруженном стержне равно силе
, линия действия которой совпадает с осью одного из стержней (рис.5.15,а). В этом случае усилие в загруженном стержне равно силе  со знаком плюс, если сила направлена от узла, или равно силе
со знаком плюс, если сила направлена от узла, или равно силе  со знаком минус, если сила направлена к узлу фермы (рис.5.15,б и в). Усилие во втором стержне равно нулю.
со знаком минус, если сила направлена к узлу фермы (рис.5.15,б и в). Усилие во втором стержне равно нулю.
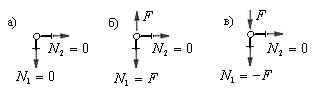
Рис.5.15
3) Узел объединяет три стержня, два из которых расположены на одной прямой, и не загружен (рис.5.16,а). В этом случае усилия в стержнях, расположенных на одной прямой равны по величине и знаку, а усилие в третьем стержне равно нулю.
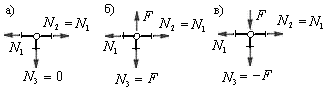
Рис.5.16
4) Узел объединяет три стержня, два из которых расположены на одной прямой, и загружен силой 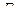 в направлении оси третьего стержня. В этом случае усилия в стержнях, расположенных на одной прямой равны по величине и знаку, а усилие в третьем стержне равно силе
в направлении оси третьего стержня. В этом случае усилия в стержнях, расположенных на одной прямой равны по величине и знаку, а усилие в третьем стержне равно силе 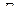 со знаком плюс, если сила направлена от узла, или равно силе
со знаком плюс, если сила направлена от узла, или равно силе 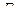 со знаком минус, если сила направлена к узлу фермы (рис.5.16,б и в).
со знаком минус, если сила направлена к узлу фермы (рис.5.16,б и в).
В заключении отметим, что метод равновесия узлов позволяет составить простые уравнения с разделенными неизвестными и вычислить усилия во всех стержнях заданной фермы, если удачно выбрать порядок рассмотрения узлов и выбрать рациональные направления осей проекций.
Следует иметь в виду, что этот метод не позволяет вычислить усилия в стержнях средних панелей ферм без предварительного определения усилий в стержнях крайних панелей.
Рассмотрим метод равновесия дисков. Он состоит в том, что заданную ферму рассекают на две части (два диска) вертикальным или наклонным сечением, которое пересекает не более трех стержней. Затем мысленно отбрасывают одну из отсеченных частей фермы, а её действие на оставшуюся часть фермы компенсируют приложением неизвестных усилий в рассеченных стержнях. Эти усилия направляют вдоль осей рассеченных стержней от узлов рассматриваемого диска.
Используя рациональные условия равновесия, составляют уравнения равновесия, из решения которых определяют усилия. Для равновесия плоского диска должны выполняться три условия равновесия. Эти условия необходимо выбирать так, чтобы каждое уравнение равновесия содержало одно неизвестное усилие.
Если два из трех рассеченных стержней пересекаются в одной точке, то эта точка является моментной для определения усилия в третьем рассеченном стержне. В этом случае уравнение равновесия составляют из условия равенства нулю суммы моментов всех сил, приложенных к рассматриваемому диску, относительно моментной точки.
Если два из трех рассеченных стержней параллельны между собой, то для определения усилия в третьем рассеченном стержне необходимо использовать условие равенства нулю суммы проекций всех сил, приложенных к рассматриваемому диску на направление оси, перпендикулярной к двум параллельным усилиям.
При его использовании можно определить усилие в любом стержне заданной фермы без предварительного определения усилий в других стержнях.
Пусть требуется определить усилия в стержнях третьей панели фермы, представленной на рис. 5.17,а. Нумерация панелей осуществляется слева направо.
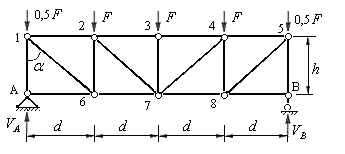
Рис.5.17
Реакции опор определяем, используя симметрию расположения опор и симметрию загружения фермы.
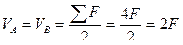
Рассекаем заданную ферму в любом месте третьей панели вертикальным сечением 1-1 (рис.5.18). Это сечение рассекает три стержня, разъединяя ферму на два диска. Левый диск состоит из двух панелей, а правый диск состоит из одной панели. Стержни третьей панели рассечены, поэтому её нет (она разрушена).
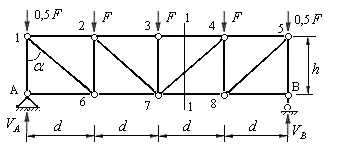
Рис.5.18
Отбрасываем мысленно левый (больший) диск, а его действие на правый диск компенсируем приложением к узлам 4 и 8 неизвестных усилий в рассеченных стержнях (рис.5.19). Усилия направляем от узлов, рассматриваемого диска.
Два из трех усилий параллельны между собой, два из них пересекаются в точке 4 и два пересекаются в точке 7.
Составляем три уравнения равновесия правого диска, используя следующие условия:
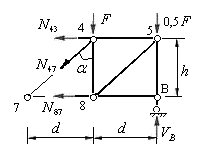
Рис.5.19
1) 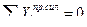

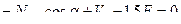

 (5.2)
(5.2)
2) 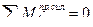

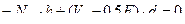

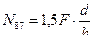 (5.3)
(5.3)
3) 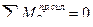

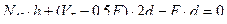

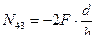 (5.4)
(5.4)
Анализируя полученные формулы, легко установить, что усилия в стержнях ферм зависят не только от внешних нагрузок, но и от геометрических размеров фермы и разновидности раскосов. С увеличением длины панели или уменьшением высоты фермы усилия возрастают. При этом усилия в стержнях нижнего пояса фермы имеют знак плюс, а усилия в стержнях верхнего пояса фермы имеют знак минус, т.е. стержни нижнего пояса растянуты, а стержни верхнего пояса сжаты. Усилия в раскосах могут быть растягивающими (в нисходящих раскосах) или сжимающими (в восходящих раскосах).
Проверим, правильно ли вычислены усилия в стержнях третьей панели рассматриваемой фермы. Для этого найдем сумму проекций всех сил, приложенных к правому диску, на горизонтальную ось:
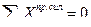

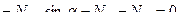
Поставляем в это уравнение значения усилий из выражений (5.2) - (5,4), получим:
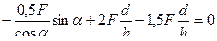 (5.5)
(5.5)
Так как 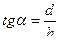 , получаем из (5.5) тождество
, получаем из (5.5) тождество 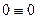 .
.
Для определения усилия в стойке 4-8 необходимо рассечь ферму на два диска наклонным сечением 2-2 , которое пересекает три стержня (рис.5.20). Отбросим левый диск фермы и его действие на правый компенсируем неизвестными усилиями в рассеченных стержнях (рис.5.21). Кроме этих усилий на диск действует внешняя сила в узле 5, и реакция опоры В. Рассмотрим равновесие этого диска.
Составим уравнение равновесия этого диска, используя условие:
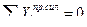

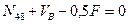

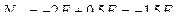 (5.6)
(5.6)
Таким образом, стойка 4-8 рассматриваемой фермы сжата усилием, модуль которого равен 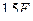 .
.
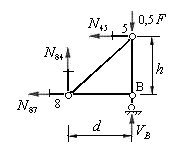
Рис.5.21
Для определения усилия в стойке 3-7 нельзя использовать метод равновесия дисков, так как нельзя рассечь ферму на две части, пересекая только три стержня (любое наклонное сечение пересекает четыре стержня фермы). Следовательно, усилие в стойке 3-7 определяется из равновесия узла 3 и равно  (смотрите 4-й случай расположения стержней в узле при загружении его силой, направленной к узлу).
(смотрите 4-й случай расположения стержней в узле при загружении его силой, направленной к узлу).
Пример 5.1 Вычислить усилия в стержнях второй панели фермы, загруженной в узлах верхнего пояса силами 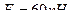 (рис.5.22). Длины панелей и высота фермы в метрах, показанные на рисунке.
(рис.5.22). Длины панелей и высота фермы в метрах, показанные на рисунке.
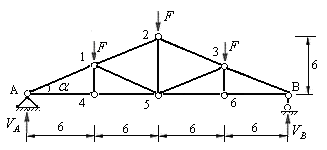
Рис.5.22
Решение:
1) Вычисляем реакции опор заданной фермы:
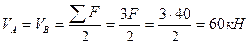
2) Рассекаем стержни второй панели фермы вертикальным сечением на два диска. Отбрасываем мысленно правый диск фермы, а его действие на левый диск заменяем усилиями в рассеченных стержнях (рис.5.23). Направляем эти усилия от узлов 1 и 4.
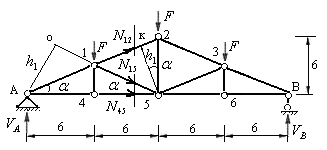
Рис.5.23
3) Составляем уравнения равновесия левого диска, используя следующие условия равновесия:
- (точка 1 является моментной для усилия в стержне 4-5)

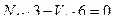

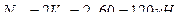
- (точка 5 является моментной для усилия в стержне 1-2)

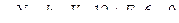 а)
а)
вычислим плечо усилия  относительно точки 5:
относительно точки 5:
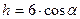 ,
, 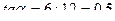 ,
,
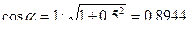 , тогда
, тогда 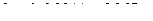
Из уравнения а) определяем 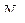 :
:
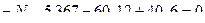

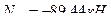
- (точка А является моментной для усилия в стержне 1-5)
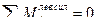

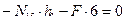

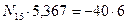

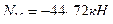
Проверяем вычисленные усилия. Для этого составим уравнение равновесия левого диска на горизонтальную ось и убедимся, что оно обращается в тождество  .
.
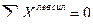

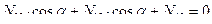

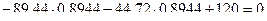

 .
.
Усилие в стойке 1-4 определяется из равновесия узла 4 и согласно 3-му частному случаю расположения стержней в узле равно нулю.
Усилие в стойке 2-5 можно определить из равновесия узла 2 или узла 5.
Рассмотрим равновесие узла 2, вырезанного из заданной фермы и загруженного, как показано на рис.5.24.
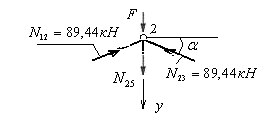
Рис.5.24
Составим уравнение равновесия узла 2, используя условие:
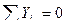




( 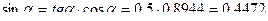 )
)
Таким образом, стойка 2-5 растянута усилием 40 кН.
Дата: 2019-02-02, просмотров: 595.