Рассмотрим трехшарнирную арку, имеющую пролет 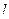 и стрелу подъема 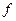(рис.4.12). Загрузим арку одной подвижной силой, имеющей единичную величину и направленной вниз. Линию движения силы  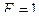принимаем горизонтальной и проходящей через ключевой шарнир арки С. При этом линия движения силы связана с осью арки в каждой точке, т.е. имеет место непосредственный способ её передачи на ось арки.

Установим силу 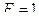 на линию движения на некотором переменном расстоянии  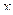от левой опорной вертикали.

Определим вертикальные реакции опор и распор арки для положения силы 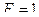, показанного на рис.4.12. Используя рациональные условия равновесия, составим уравнения равновесия:

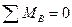
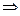
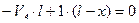- , откуда:

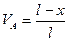                                                                                                          (4.21)

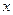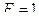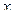                   Из полученного уравнения (4.21) следует, что вертикальная реакция левой опоры арки линейно зависит от , т.е. от положения силы  на линии движения. График этого уравнения является линией влияния . Уравнение (4.21) справедливо в интервале изменения  от 0 до 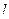. Вычисляем две ординаты линии влияния:

                                          - при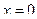

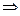
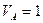
                                          - при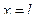                               

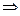
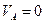
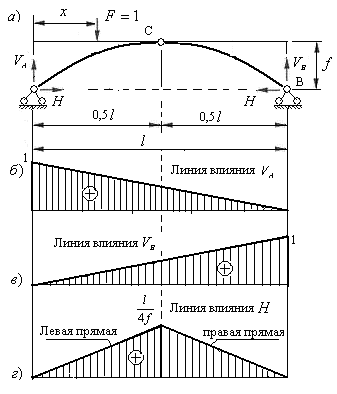
                                              Рис.4.12

       На рис.(4.12,б) построена линия влияния 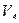, которая полностью совпадает с линией влияния вертикальной реакции левой опоры однопролетной балки на двух шарнирных опорах.

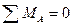
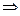
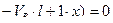  - , откуда:

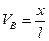                                                                                                         (4.22)      

       Уравнение (4.22) является уравнением линии влияния вертикальной реакции правой опоры арки 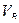, которое существует в интервале изменения  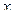от 0 до 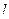. График этого уравнения (линия влияния 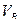) построен на рис.4.12,в. Легко заметить, что линия влияния  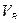совпадает с линией влияния реакции правой опоры однопролетной балки.

       Составим уравнение левой прямой линии влияния распора арки, используя условие равновесия правой полуарки относительно левой, т.е. условие:

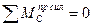
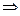
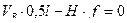- , откуда, с учетом уравнения (4.22), получаем уравнение левой прямой линии влияния распора арки :

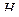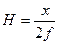                                                                                                      (4.23)

Левая прямая ограничивает линию распора арки на участке между левой опорой и ключевым шарниром, т.е. в интервале изменения 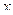 от 0 до 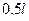. Для построения левой прямой вычисляем две ординаты линии влияния распора арки :

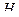- при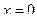

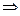
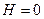
                                      - при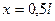

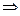
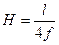
Напомним, что ординаты линии влияния любого силового фактора, имеющие знак плюс, откладываем вверх от нулевой прямой, а ординаты, имеющие знак минус, откладываем вниз от той же прямой.

 Нулевая прямая линии влияния проводится горизонтально под аркой в пределах её пролета. На рис.4.12,г построена левая прямая распора арки, используя вычисленные ординаты.

       Переместим силу 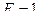 на правую полуарку и составим уравнение правой прямой линии влияния распора арки, используя условие равновесия левой полуарки относительно правой, т.е. условие:

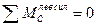
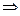
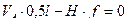- , откуда, с учетом уравнения (4.21), получаем уравнение правой прямой линии влияния распора арки :

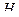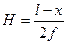                                                                                                (4.24)

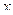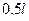Правая прямая ограничивает линию распора арки на участке между ключевым шарниром и правой опорой и т.е. в интервале изменения  от  до 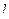. Для построения правой прямой вычисляем две ординаты линии влияния распора арки :

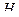- при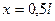

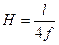
- при

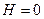
Откладываем эти ординаты соответственно под ключевым шарниром и правой опорой и соединяем их правой прямой (рис.4.12,г), в результате получаем линию влияния распора арки.

Анализируя линию влияния распора арки, легко установить, что она ограничена двумя прямыми, которые пересекаются под ключевым шарниром арки и имеют нулевые точки под соответствующими опорами. Максимальная ордината линии влияния распора арки равна отношению длины пролета арки к учетверенной стреле подъема арки, т.е. вычисляется по формуле:

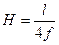                                                            (4.25)

 Поэтому при решении задач нет необходимости составлять уравнения левой и правой прямых линии влияния распора арки. Достаточно вычислить ординату линии влияния под ключевым шарниром по формуле (4.25), отложить её от нулевой прямой в произвольно выбранном масштабе и соединить с нулевыми точками под опорами арки.

Легко заметить также, что линия влияния распора арки совпадает по виду с линией влияния изгибающего момента в сечении однопролетной балки на двух шарнирных опорах, взятом посредине пролета. Если пролеты арки и балки одинаковы, то линию влияния распора арки можно построить путем деления ординат линии влияния балочного изгибающего момента в сечении, взятом под ключевым шарниром арки на стрелу подъема арки.