В предыдущей главе приведена краткая характеристика статически неопределимых рам, из которой следует, что все связи стержневых систем обладают двумя характеристиками: статической и кинематической. Усилия, возникающие в связях системы, являются их статической характеристикой, а перемещения, которые имеют или допускают связи, являются их кинематической характеристикой.
Если при расчете статически неопределимых стержневых систем принимаются кинематические характеристики связей, то метод расчета называют методом перемещений.
Для расчета рам необходимо установить независимые перемещения, подлежащие определению. Рамы состоят из стержней, объединенных между собой в узлах жестко или шарнирно. При загружении рам жесткие узлы получают некоторые повороты и линейные смещения в направлениях, допускаемых связями.
В методе перемещений принято допущение о нерастяжимости стержней, поэтому все узлы, расположенные на одной прямой имеют одинаковые перемещения в направлении этой прямой.
Если известны углы поворота жестких узлов и их линейные перемещения, то для каждого стержня рамы можно определить внутренние усилия и построить их эпюры.
Обозначим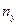 
- число жестких узлов рамы, а 
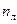– число независимых линейных смещений групп узлов, расположенных на одной горизонтальной, вертикальной или наклонной прямой.
Тогда общее число неизвестных метода перемещений будет определяться по формуле:
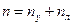(8.1)
Число 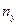определяется простым подсчетом жестких узлов рамы, а для определения числа 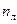необходимо образовать условную шарнирную схему рамы, путем введения полных шарниров во все жесткие узлы и защемляющие опоры заданной рамы и установить степень её геометрической изменяемости.
В главе 1 установлена формула, позволяющая установить степень геометрической изменяемости стержневых систем образованных по первому варианту:
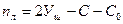, (8.2)
Где: Уш - число шарнирных узлов условной шарнирной схемы;
С - число стержней, которые объединяют эти узлы между собой;
Со - число опорных стержней, препятствующих линейным перемещениям узлов в любом возможном направлении.
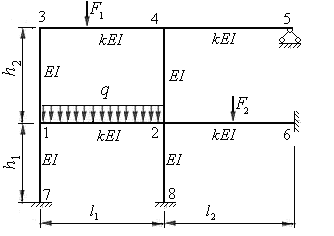
Рис.8.1
На рисунках 8.1 и 8.2 представлены расчетные схемы плоских статически неопределимых рам. В дальнейшем будем называть их рама 1 и рама 2. Рама 1 состоит из восьми прямолинейных стержней, объединенных между собой жесткими узлами 1,2,3.4 и закрепленных при помощи трех защемляющих опор и одной шарнирно неподвижной опоры. Такая рама носит название рамы с не смещающимися узлами. Опоры и стержни рамы исключают возможность линейных смещений её узлов, как в горизонтальном направлении, так и в вертикальном направлении.
Рама 2 также состоит из восьми стержней, но имеет два жестких узла 1, 3 и два шарнирных узла 0, 5. В отличие от рамы 1, рама 2 имеет две защемленные опоры и две шарнирно подвижные опоры. Такая рама является рамой со смещающимися узлами. Узлы рамы 2 имеют горизонтальные перемещения.
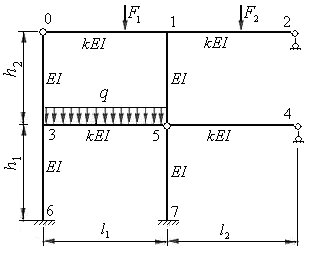
Рис.8..2
На расчетных схемах рам 1 и 2 показаны возможные варианты загружения стержней.
Установим число независимых неизвестных метода перемещений (степень кинематической неопределимости) для этих рам. Рама 1 имеет 4 жестких узла, следовательно, 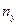= 4. Для рамы с не смещающимися узлами число 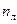=0. Следовательно, кинематическая неопределимость рамы 1 определяется только первым слагаемым правой части формулы (8.1),т.е. она имеет четыре неизвестных угла поворота жестких узлов и является статически неопределимой системой с четырьмя неизвестными метода перемещений.
Для рамы 2 со смещающимися узлами число жестких узлов равно 2 ( 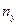=2), а число 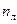определяется как степень геометрической изменяемости условной шарнирной схемы, образованной из заданной рамы путем введения полных цилиндрических шарниров во все жесткие узлы и защемляющие опоры этой рамы.
На рис.8.3 представлена условная шарнирная схема рамы 2. Она является геометрически изменяемой. Степень геометрической изменяемости определяется по формуле:
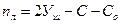(8.2)
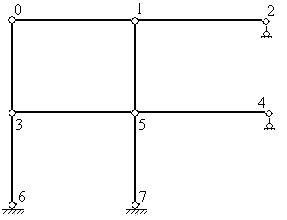
Рис. 8..3
Анализируем условную шарнирную схему рамы. Она состоит из четырех шарнирных узлов (Уш=4), обозначенных на рис.8.3 цифрами 0,1,3,5; четырёх стержней С=4 (стержни 0-1, 1-5, 0-3, 3-5), которые объединяют эти узлы, и двух опорных стержней Со=2 (стержни 3-6 и 5-7), которые препятствуют смещению узлов в вертикальном направлении. Таким образом, по формуле (8.2) получаем:
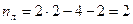
Условная шарнирная схема позволяет установить не только количество неизвестных линейных смещений, но и их направления. По рис.8.3 легко установить, что узлы 0, 1 и опора 2 могут сместиться горизонтально на одну и ту же величину, в силу принятого допущения о нерастяжимости стержней рамы.
Аналогично узлы 3, 5 и опора 4 могут также сместиться горизонтально на некоторую величину, отличную в общем случае от первого горизонтального перемещения.
Таким образом, общее число неизвестных метода перемещений для рамы 2 устанавливаем по формуле (8.1) и оно также как и для рамы 1 равно 4.
Примечания: 1) Стержни рамы, которые закреплены шарнирно подвижными опорами в направлении собственных осей (например, стержни 1-2 и 5-4 рамы 2 не являются опорными и при определении числа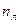 
не учитываются;
2) если два стержня препятствуют смещению узлов рамы в одном направлении (т.е. являются опорными стержнями, расположенными на одной прямой), то при определении числа 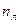учитывается только один из них.
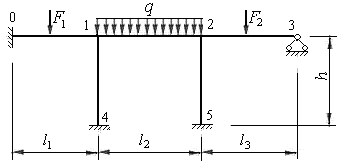
Рис.8.4
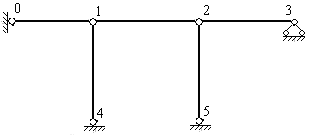
Рис.8.5
Например, при установлении числа неизвестных метода перемещений для рамы 3 (рис.8.4) находим число 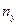=2 (жесткие узлы 1,2), затем образуем условную шарнирную схему (рис.8.5) и находим число 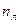по формуле (8.2). При этом учитываем только три опорных стержня из четырех (стержень 2-3 не учитываем, так как он дублирует функции опорного стержня 0-1).
Следовательно, Уш=2 , С=1, Со=3, тогда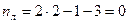 
.
Таким образом, рама 3 является два раза кинематически неопределимой (неизвестными являются углы поворота жестких узлов).
8.2 Основная системы (ОС) метода перемещений.
Основная система метода перемещений образуется путем введения плавающих заделок в жесткие узлы заданной рамы и шарнирно стержневых связей в направлении возможных линейных перемещений её узлов и стержней.
Плавающие заделки исключают повороты жестких узлов, но не препятствуют их линейным перемещениям. Этим они отличаются от жестких защемляющих опор.
Шарнирно стержневые опорные связи исключают только линейные перемещение в направлениях осей этих связей.
Для образования основной системы рамы 1 необходимо ввести в её жесткие узлы 1,2,3,4 плавающие заделки (рис.8.6).
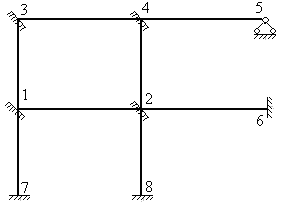
Рис.8.6
Для образования основной системы рамы 2 необходимо ввести в жесткие узлы 1 и 3 плавающие заделки и установить шарнирно-стержневые связи на горизонтальные перемещения опор 1 и 4 (рис.8.7).
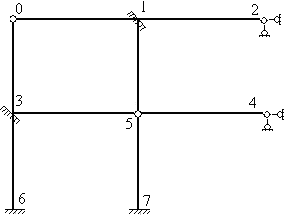
Рис.8.7
Для образования основной системы рамы 3 необходимо ввести в жесткие узлы 1 и 2 плавающие заделки (рис.8.8). Таким образом, в методе перемещений возможен только один вариант основной системы.
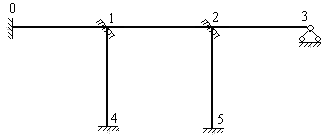
Рис.8.8
Анализируя основную систему для любой рамы легко заметить, что она:
1) является статически неопределимой с более высокой степенью неопределимости, чем заданная рама;
2) является кинематически определимой, так как её узлы не имеют ни угловых, ни линейных перемещений;
3) состоит из отдельных стержней двух типов: стержней с двумя защемленными опорами и стержней с одной защемленной, а другой шарнирной опорами. Каждый из этих стержней является статически неопределимым. Но для таких стержней легко построить эпюры изгибающих моментов от единичных углов поворота жестких узлов, единичных линейных смещений одной из опор в направлении, перпендикулярном осям стержней, а также внешних нагрузок, представленных сосредоточенными силами или моментами и равномерно распределенными нагрузками.
8.3. Эквивалентная система (ЭС) метода перемещений.
Эквивалентная система образуется путем приложения к основной системе заданных нагрузок, неизвестных углов поворота плавающих заделок (жестких узлов) и линейных перемещений групп узлов в направлении их подвижности (в направлении оси введенной шарнирно-стержневой связи). Заданные нагрузки могут быть приложены ко всем стержням рамы, или к отдельным из них.
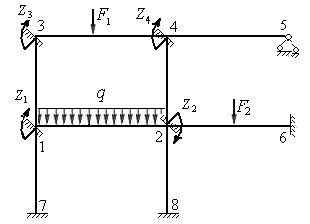
Рис.8.9
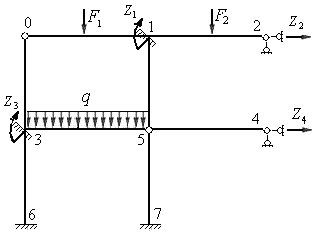
Рис.8.10
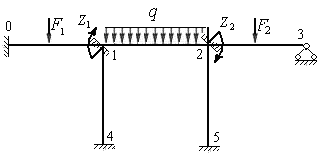
Рис.8.11
Неизвестные углы поворота направляем по ходу часовой стрелки, неизвестные горизонтальные перемещения - вправо, а неизвестные вертикальные перемещения - вниз. Неизвестные метода перемещений, независимо от их характера, обозначаем буквой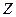 
с индексом, который соответствует номеру узла или номеру связи на линейное перемещение, т.е. 
, 
, 
, 
. ..
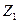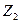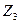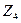На рис. 8.9 – 8.11 изображены эквивалентные системы рам 1, 2 и 3 соответственно. В дополнительно введенных связях эквивалентной системы возникают реактивные усилия от действия заданных нагрузок, углов поворота жестких узлов и линейных перемещений групп узлов. В плавающих заделках возникают реактивные моменты, а в шарнирных связях - сосредоточенные силы.
Сопоставляя эквивалентную систему с заданной рамой, легко установить, что их деформированные состояния будут совпадать, если реактивные усилия в дополнительно введенных связях эквивалентной системы будут равными нулю, т.е.:
, 
, 
, 
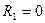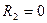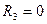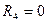… (8.3)
Условия (8.3) называются условиями эквивалентности метода перемещений.
Дата: 2019-02-02, просмотров: 387.
