Канонические уравнения метода перемещений вытекают из условий эквивалентности (8.3) при использовании принципа независимости всех силовых и кинематических нагрузок, приложенных к эквивалентной системе.

Составим первое каноническое уравнение метода перемещений для рамы с четырьмя неизвестными, используя условие .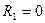

Реактивное усилие 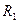 возникает в дополнительно введенной связи 1 эквивалентной системы от действия четырех неизвестных 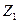, , 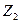,  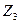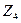и заданных нагрузок. Тогда, по принципу независимости их действия получим:

                                                                    (8.4)

В правой части равенства (8.4) реактивные усилия имеют два индекса. Первый из них обозначает порядковый номер введенной связи эквивалентной системы, в которой усилие, а второй индекс указывает вид нагрузки, от действия которой оно возникает, т.е.:

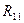 - есть реактивное усилие, возникающее в дополнительно введенной связи 1 эквивалентной системы (первый индекс 1) от действия  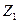(второй индекс 1).

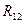 - есть реактивное усилие, возникающее в дополнительно введенной связи 1 эквивалентной системы (первый индекс 1) от действия  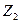(второй индекс 2), и т.д.

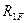 - есть реактивное усилие, возникающее в дополнительно введенной связи 1 эквивалентной системы (первый индекс 1) от действия всех заданных нагрузок (второй индекс ).

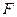       Первые четыре слагаемые правой части равенства (8.4) определяются умножением неизвестных перемещений на единичные реактивные усилия, возникающие в тех же связях основной системы, загруженной единичными перемещениями, т.е.:     , , , .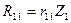

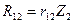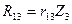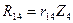       Подставим эти значения в равенство (8.4) и приравняем к нулю сумму всех слагаемых правой части, в результате получим первое каноническое уравнение метода перемещений:

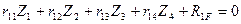
       Второе и последующие уравнения составляем аналогично первому уравнению, используя второе и последующие условия эквивалентности (8.3) и принцип независимости действий внешних нагрузок. Число таких уравнений равно степени кинематической неопределимости заданной рамы, т.е. числу неизвестных метода перемещений. Все они составляют систему канонических уравнений.

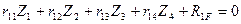
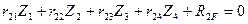
       Например, для рам 1 и 2 с четырьмя неизвестными метода перемещений получаем систему четырех канонических уравнений 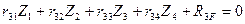(8.5):

                                                          (8.5)

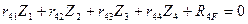
Для рамы 3 с двумя неизвестными метода перемещений составляются два канонических уравнения:

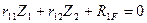
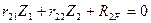                                                                                 (8.6)

Каждое каноническое уравнение метода перемещений является отрицанием наличия реактивного момента в дополнительно введенной плавающей заделке эквивалентной системы, или реактивной сосредоточенной силы в дополнительно введенной шарнирно стержневой связи той же системы.

Обратим внимание на то, что система канонических уравнений зависит лишь от степени кинематической неопределимости рамы и не зависит от характера неизвестных метода перемещений. Но физический смысл их определяется характером вводимых связей основной системы. Так, например, для рамы 1 все четыре канонических уравнения имеют одинаковый физический смысл – отрицание наличия реактивных моментов во всех четырех дополнительно введенных плавающих заделках эквивалентной системы. Для рамы 2 два канонических уравнения (первое и третье) имеют такой же физический смысл, что и для рамы 1, а два других уравнения (второе и четвертое) отрицают наличие горизонтальных реактивных сил в дополнительно введенных шарнирно стержневых связях.  

Понимание физической сущности канонических уравнений позволяет правильно установить физический смысл каждого коэффициента и свободного члена системы уравнений и выбрать рациональный метод их определения. Методы определения коэффициентов и свободных членов канонических уравнений изложены в параграфе 8.7.