Шпренгельные фермы состоят из простых плоских ферм, называемых основными, и дополнительных шарнирно стержневых устройств, называемых шпренгелями. Шпренгели позволяют передавать нагрузки, приложенные к стержням, на узлы основных ферм.
Если шпренгель передает приложенную к нему нагрузку на узлы загруженного пояса основной фермы, то его называют одноярусным. Если же шпренгель передает приложенную к нему нагрузку на узлы не загруженного пояса основной фермы, то его называют двухъярусным.
Рассмотрим простую ферму с параллельными поясами и раскосной решеткой, загруженную в узлах верхнего пояса силами 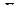 и силами
и силами 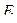 вне узлов (рис.5.25). Стержни этой фермы называют стержнями первой категории, или стержнями основной фермы.
вне узлов (рис.5.25). Стержни этой фермы называют стержнями первой категории, или стержнями основной фермы.
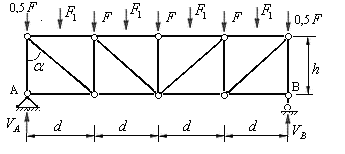
Рис.5.25
Силы 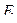 вызывают изгиб стержней верхнего пояса фермы, что не допускается в фермах. Поэтому силы
вызывают изгиб стержней верхнего пояса фермы, что не допускается в фермах. Поэтому силы 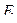 необходимо передать на смежные узлы верхнего (или нижнего) пояса фермы. Пусть силы
необходимо передать на смежные узлы верхнего (или нижнего) пояса фермы. Пусть силы 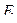 в первой и четвертой панелях фермы требуется передать на узлы верхнего пояса фермы, а во второй и третьей панелях те же силы требуется передать на узлы нижнего пояса фермы. Для этого врезают шарниры в поясные стержни и в раскосы на линиях действия сил
в первой и четвертой панелях фермы требуется передать на узлы верхнего пояса фермы, а во второй и третьей панелях те же силы требуется передать на узлы нижнего пояса фермы. Для этого врезают шарниры в поясные стержни и в раскосы на линиях действия сил 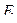 в каждой панели фермы, и эти шарниры объединяют между собой стержнями. Получают дополнительные стойки, принадлежащие шпренгелям. Затем шарниры, расположенные на раскосах основной фермы соединяют с соседними узлами верхнего или нижнего поясов. В результате получают раскосы одноярусных шпренгелей (в первой и четвертой панелях) и раскосы двухъярусных шпренгелей (во второй и третьей панелях фермы рис.5.26). Стойки и раскосы шпренгелей помечены на рис.5.26 двумя черточками. Эти стержни относятся ко второй категории шпренгельных ферм.
в каждой панели фермы, и эти шарниры объединяют между собой стержнями. Получают дополнительные стойки, принадлежащие шпренгелям. Затем шарниры, расположенные на раскосах основной фермы соединяют с соседними узлами верхнего или нижнего поясов. В результате получают раскосы одноярусных шпренгелей (в первой и четвертой панелях) и раскосы двухъярусных шпренгелей (во второй и третьей панелях фермы рис.5.26). Стойки и раскосы шпренгелей помечены на рис.5.26 двумя черточками. Эти стержни относятся ко второй категории шпренгельных ферм.
Два дополнительно введенные шарнира каждой панели фермы объединяют с соседними узлами верхнего или нижнего пояса. Эти стержни принадлежат шпренгелям, но совмещаются со стержнями основной фермы, образуя стержни третьей категории шпренгельной фермы. На рис.5.26 эти стержни показаны двойными линиями (сплошными и штриховыми).
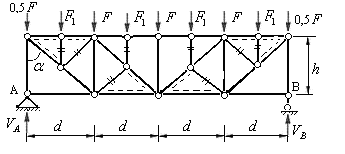
Рис.5.26
В результате получаем конструкции одноярусного (рис.5.27,а) и двухъярусного (рис.5.27,б) шпренгелей. Опорами одноярусного шпренгеля являются соседние узлы загруженного (в рассматриваемом случае верхнего) пояса фермы, а опорами двухъярусного шпренгеля являются соседние узлы незагруженного пояса фермы (нижнего).
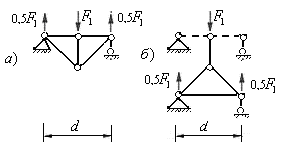
Рис.5.27
При загруженном нижнем поясе фермы, сосредоточенные силы, приложенные вне узлов, можно также передать на узлы нижнего или верхнего пояса с помощью одноярусных или двухъярусных шпренгелей. На рис.5.28 показаны конструкции таких шпренгелей.
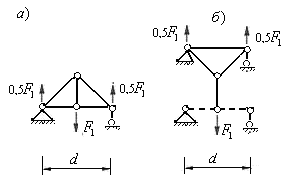
Рис.5.28
Для определения усилий в стержнях шпренгельных ферм необходимо:
1) Образовать основную ферму путем удаления всех шпренгелей и определить нагрузки, действующие на её узлы.
В узлах, на которые опирались удаленные шпренгели, следует приложить силы равные и противоположно направленные реакциям опор удаленных шпренгелей, а также заданные силы. Если принять 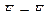 , то основная ферма при расчете шпренгельной фермы, представленной на рис. 5.26, будет иметь нагрузки, показанные на рис.5.29.
, то основная ферма при расчете шпренгельной фермы, представленной на рис. 5.26, будет иметь нагрузки, показанные на рис.5.29.
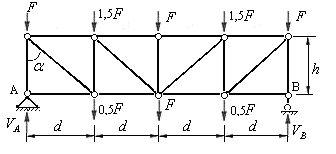
Рис.5.29
Реакции опор и усилия в стержнях основной фермы (усилия в стержнях первой категории) определяются, как и при расчете простых ферм.
2) Усилия в стержнях второй категории определяют из расчета шпренгелей по методу равновесия узлов. Если во всех панелях заданной фермы установлены однотипные шпренгели, то определяются усилия в стержнях одного из них.
3) Усилия в стержнях третьей категории равны алгебраической сумме усилий в соответствующих стержнях основной формы и шпренгелей.
Пример 5.2 Определить усилия в стержнях второй панели заданной фермы с двухъярусными шпренгелями (рис.5.30). Для расчета принять 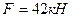 ,
, 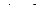 ,
, 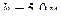 .
.
Решение: Обозначим опорные узлы фермы буквами А и В, а узлы второй панели заданной фермы – цифрами.
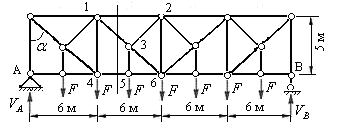
Рис.5.30
Образуем основную ферму, удалив двухъярусные шпренгели всех четырех панелей. Силы, приложенные к узлам шпренгелей, передаются на узлы верхнего пояса основной фермы. На рис.5.31 показаны силы, действующие на узлы основной фермы.
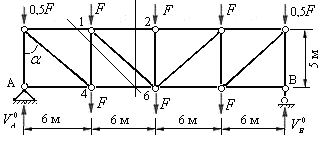
Рис.5.31
Вычисляем реакции опор основной фермы, используя условия симметрии её загружения.
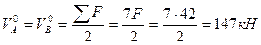
Определяем усилия в стержнях второй панели основной фермы, т.е. в стержнях 1-2, 1-6, 4-6, 1-4, и 2-6. Усилие в стойке 2-6 определяется из равновесия узла 2 и равно: 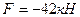 . Усилия в остальных стержнях определяем методом равновесия дисков. Рассекаем ферму сквозным вертикальным сечением на два диска, отбрасываем правый диск, а его действие на левый заменяем неизвестными усилиями в рассеченных стержнях (рис.5.32).
. Усилия в остальных стержнях определяем методом равновесия дисков. Рассекаем ферму сквозным вертикальным сечением на два диска, отбрасываем правый диск, а его действие на левый заменяем неизвестными усилиями в рассеченных стержнях (рис.5.32).
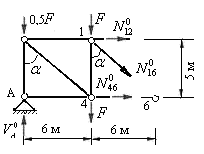
Рис.5.32
Составляем уравнения равновесия левого диска, используя следующие условия равновесия:
- (точка 1 является моментной для усилия в стержне 4-6)
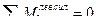

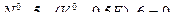

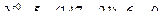

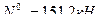
- (точка 6 является моментной для усилия в стержне 1-2)
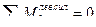

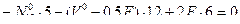

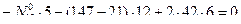

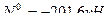
Для определения усилия 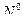 составляем уравнение равновесия, используя условие:
составляем уравнение равновесия, используя условие: 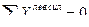

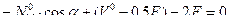

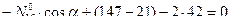

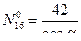
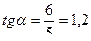


 ,
, 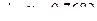 ,
,
тогда: 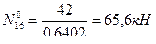
Проверяем вычисленные усилия. Для этого составляем уравнение равновесия рассматриваемого диска, используя условие равновесия:
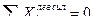

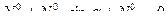

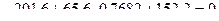

 .
.
Определяем усилие в стойке 1-4 основной фермы. Для этого рассекаем ферму на 2 диска наклонным сечением, рассекающим три стержня, включая стойку 1-4.
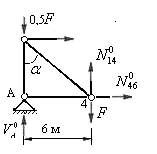
Рис.5.33
Рассматриваем левый диск (рис.5.33) и составляем уравнение равновесия, используя условие: 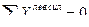

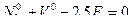

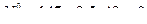

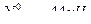
Определяем усилия в стержнях шпренгеля второй панели заданной фермы (рис.5.34,а), используя метод равновесия узлов. Из равновесия узла 5 следует, что усилие в стойке 5-3 равно силе 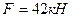 , т.е стойка 5-3 растянута.
, т.е стойка 5-3 растянута.
Для определения усилий в стержнях 1-2 и 1-3 шпренгеля вырезаем узел 1, выбираем рациональные направления осей проекций и составляем уравнения равновесия этого узла:
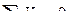

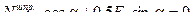


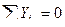



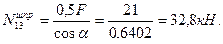
Усилие в стержне 2-3 шпренгеля равно усилию в его стержне 1-3.
Вычисляем усилия в стержнях 1-2 и 1-3 заданной фермы:
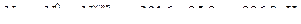
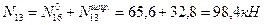
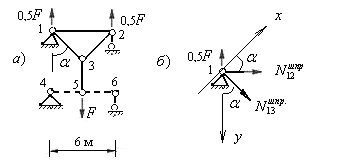
Рис.5.34
Проверим, правильно ли вычислены эти усилия. Для этого рассечем заданную ферму во второй панели так, чтобы были рассечены три стержня (рис.5.30) и рассмотрим равновесие левого диска, загруженного силами, показанными на рис.5.35.
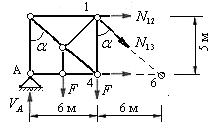
Рис.5.35
Составим два уравнения равновесия, используя условия:
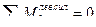

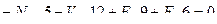

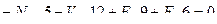

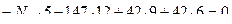

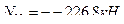
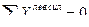

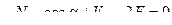

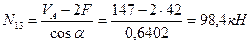
Таким образом, усилия определены правильно.
Вопросы для самоконтроля полученных знаний.
1. Что называется фермой?
2. Какие усилия появляются в элементах ферм н почему?
3. Почему фермы более экономичны по сравнению с балками?
4. Какие элементы различают в фермах?
5. По каким признакам классифицируют фермы?
6. Какие методы применяют для определения усилий в стержнях ферм?
7. Как применяется способ вырезания узлов для ручного счета? В чем достоинства и недостатки этого способа?
8. Приведите частные случаи равновесия узлов.
9. В каком случае рационально определять усилия способом моментной точки?
10. Как зависят усилия в поясах балочной фермы от ее высоты?
11. Как изменяются усилия в поясах балочной фермы вдоль ее пролета?
12. Когда удобно применять способ проекций? В чем отличие характера работы восходящих и нисходящих раскосов балочной фермы?
13. Как изменяются усилия в раскосах балочной фермы вдоль ее пролета?
14. Приведите примеры использования для расчета ферм балочных усилий.
15. В каких случаях применяется способ замкнутого сечения?
16. Как применяется способ двух сечений?
17. Что такое шпренгельная ферма?
18. С какой целью применяют шпренгели?
19. Чем отличается работа двухъярусных шпренгелей от одноярусных?
20. На какие типы делятся стержни шпренгельных ферм?
21. Каковы особенности определения усилий и построения линий влияния в шпренгельных фермах?
Глава 6. Работа внешних сил и внутренних усилий. Основные теоремы и методы определения упругих перемещений.
6 .1. Работа внешних статически нарастающих сил.
Рассмотрим упругую стержневую систему, загруженную обобщенной статически нарастающей силой 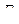 (рис.6.1).
(рис.6.1).
В направлении этой силы возникает обобщенное перемещение  .
.
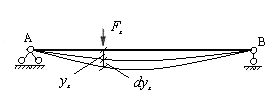
Рис.6.1
Под термином «обобщенная» следует понимать любую силу или момент, которые могут совершать работу на перемещениях упругой системы по их направлению.
Статически нарастающая сила меняет свою величину от нуля до конечного значения очень медленно на протяжении большого промежутка времени.
В упругой стадии деформирования стержневой системы имеет место линейная пропорциональная зависимость между перемещением и силой на любом этапе изменения силы и перемещения, т. е.:
 ,
, 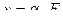 (6.1)
(6.1)
Дадим силе 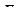 элементарное приращение
элементарное приращение 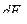 , тогда перемещение
, тогда перемещение  получит элементарное приращение
получит элементарное приращение 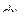 , на котором сила
, на котором сила 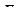 совершит элементарную работу равную произведению силы на перемещение, т.е.:
совершит элементарную работу равную произведению силы на перемещение, т.е.:
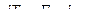 (6.2)
(6.2)
Найдем 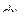 , продифференцировав первое равенство зависимостей (6.1):
, продифференцировав первое равенство зависимостей (6.1):
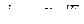
Подставим это значение в равенство (6.2) и проинтегрируем полученное выражение в интервале изменения силы 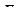 от нуля до конечного значения
от нуля до конечного значения 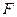 , в результате получим:
, в результате получим:
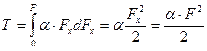 (6.3)
(6.3)
С учетом второго равенства зависимостей (6.1) получим:
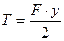 (6.4)
(6.4)
Таким образом, работа статически нарастающей силы равна половине произведения конечного значения силы на конечное значение упругого перемещения, вызванного силой по её направлению.
6 .2. Работа внутренних усилий (потенциальная энергия стержневой системы).
При загружении плоской упругой системы внешними силами, в её поперечных сечениях возникают изгибающие моменты, продольные силы и поперечные силы. Они непрерывно меняются по длине каждого участка каждого стержня, т.е. являются функциями переменной 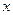 .
.
Рассмотрим упругую балку, загруженную в вертикальной плоскости произвольной силой 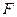 , достигшей конечного значения (рис.6.2). Выделим элемент балки длиной
, достигшей конечного значения (рис.6.2). Выделим элемент балки длиной 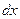 , взятый на переменном расстоянии от начала участка.
, взятый на переменном расстоянии от начала участка.
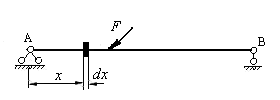
Рис.6.2
На этот элемент будут действовать внутренние усилия  ,
, 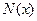 ,
, 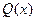 , показанные на рис.6.3.
, показанные на рис.6.3.
Эти усилия могут рассматриваться как внешние силы, действующие на элемент длиной 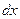 упругой системы. Кроме того, они являются взаимно ортогональными, т.е. такими силами, которые совершают работу только на собственных перемещениях. Изгибающие моменты вызывают взаимные повороты смежных торцов выделенного элемента балки. Если левую грань элемента жестко закрепить (рис.6.4), то правая грань получит поворот в направлении момента
упругой системы. Кроме того, они являются взаимно ортогональными, т.е. такими силами, которые совершают работу только на собственных перемещениях. Изгибающие моменты вызывают взаимные повороты смежных торцов выделенного элемента балки. Если левую грань элемента жестко закрепить (рис.6.4), то правая грань получит поворот в направлении момента  на угол
на угол 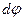 , величина которого определяется по формуле, известной из сопротивления материалов:
, величина которого определяется по формуле, известной из сопротивления материалов:
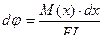
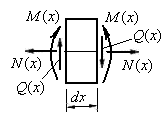
Рис.6.3
Изгибающий момент  совершает на этом перемещении элементарную работу, равную:
совершает на этом перемещении элементарную работу, равную:
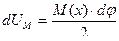 , или с учетом предыдущей зависимости:
, или с учетом предыдущей зависимости:
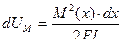 (6.5)
(6.5)
Для вычисления полной работы, которую совершают изгибающие моменты заданной стержневой системы, необходимо выражение (6.5) проинтегрировать по всем участкам и найти алгебраическую сумму этих интегралов, т.е.:
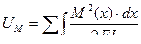 (6.6)
(6.6)
Аналогично, продольные силы 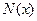 вызывает продольные деформации элемента системы и совершает на этих перемещениях работу, численно равную:
вызывает продольные деформации элемента системы и совершает на этих перемещениях работу, численно равную:
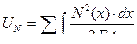 (6.7)
(6.7)
Поперечные силы 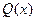 вызывают взаимные сдвиги граней элемента системы в направлениях, перпендикулярных осям стержней, и совершают на этих перемещениях работу, определяемую по формуле:
вызывают взаимные сдвиги граней элемента системы в направлениях, перпендикулярных осям стержней, и совершают на этих перемещениях работу, определяемую по формуле:
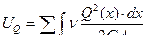 (6.8)
(6.8)
Полная работа всех внутренних усилий (потенциальная энергия стержневой системы) определяется суммой работ, совершаемых каждым усилием, т.е.:
 (6.9)
(6.9)
В формуле (6.9) содержатся следующие параметры сечений стержневой системы:
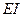 - изгибная жесткость поперечных сечений стержней на отдельных участках;
- изгибная жесткость поперечных сечений стержней на отдельных участках;
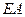 - жесткость сечений стержней при их растяжении (сжатии);
- жесткость сечений стержней при их растяжении (сжатии);
 - жесткость сечений стержней при сдвиге;
- жесткость сечений стержней при сдвиге;
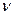 - коэффициент, учитывающий неравномерность распределения касательных напряжений по высоте сечений. Его величина зависит от формы поперечного сечения.
- коэффициент, учитывающий неравномерность распределения касательных напряжений по высоте сечений. Его величина зависит от формы поперечного сечения.
Примечания:
1) Потенциальная энергия балочных и рамных систем вычисляется по формуле (6.6), так как влияние продольных и поперечных сил в таких системах очень мало по сравнения с влиянием изгибающих моментов;
2) Потенциальная энергия ферм, в стержнях которых возникают только продольные усилия, вычисляется по формуле (6.7).
3) Влияние поперечных сил учитывается при вычислении потенциальной энергии некоторых типов пологих арок.
6.3. Свойства потенциальной энергии.
Потенциальная энергия деформации плоской стержневой системы вычисляется по формуле (6.9) и обладает следующими свойствами:
1) Потенциальная энергия является однородной квадратичной функцией внутренних усилий  ,
, 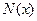 ,
, 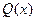 ;
;
2) Потенциальная энергия всегда положительна, так как она зависит от квадратов внутренних усилий;
3) При вычислении потенциальной энергии неприменим принцип независимости действия внешних сил, так как квадрат суммы не равен сумме квадратов;
4) Количество энергии не зависит от порядка загружения стержневой системы, а определяется конечным состоянием её загружения.
6.4. Универсальное обозначение упругих перемещений.
Следует различать полные и единичные упругие перемещения сечений системы.
Полные перемещения возникают от действия нагрузок, отличных от 1 (единицы) и обозначаются прописной буквой 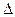 (дельта) греческого алфавита, а единичные перемещения возникают от действия сосредоточенных сил или моментов равных по модулю 1 (единице) и обозначаются строчной буквой
(дельта) греческого алфавита, а единичные перемещения возникают от действия сосредоточенных сил или моментов равных по модулю 1 (единице) и обозначаются строчной буквой 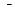 (дельта).
(дельта).
Перемещения приписывают два индекса (буквенных или числовых) внизу. Например: 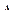 или
или 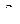 (
( 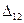 или
или 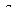 ).
).
Первый индекс указывает направление перемещения, а второй – указывает нагрузку, от действия которой оно возникает. Так, перемещение 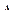 имеет направление обобщенной силы
имеет направление обобщенной силы  и возникает от действия обобщенной силы
и возникает от действия обобщенной силы 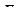 . Перемещение
. Перемещение 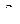 имеет направление обобщенной силы
имеет направление обобщенной силы  и возникает от действия обобщенной силы
и возникает от действия обобщенной силы 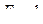 .
.
Аналогично, перемещение 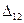 имеет направление обобщенной силы
имеет направление обобщенной силы  и возникает от действия обобщенной силы
и возникает от действия обобщенной силы  , а перемещение
, а перемещение 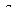 также имеет направление обобщенной силы
также имеет направление обобщенной силы  , но возникает от действия обобщенной силы
, но возникает от действия обобщенной силы 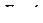 .
.
6.5. Понятие о дополнительных (возможных) работах внешних сил и внутренних усилий.
Рассмотрим упругую балку на двух шарнирных опорах (рис.6.4). Загрузим её силой  . В результате изгиба балки точка приложения силы
. В результате изгиба балки точка приложения силы  получит вертикальное перемещение
получит вертикальное перемещение 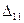 после достижения статически нарастающей силой конечного значения.
после достижения статически нарастающей силой конечного значения.

Рис.6.4
Загрузим дополнительно балку силой  , приложив её к изогнутой оси. Тогда точка приложения силы
, приложив её к изогнутой оси. Тогда точка приложения силы  дополнительно переместится на величину
дополнительно переместится на величину 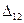 и сила
и сила  , будучи постоянной, совершит работу равную произведению модуля силы на перемещение, т.е.:
, будучи постоянной, совершит работу равную произведению модуля силы на перемещение, т.е.:
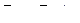 (6.10)
(6.10)
Работа 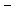 называется дополнительной работой силы
называется дополнительной работой силы  на перемещении, вызванном по её направлению действием силы
на перемещении, вызванном по её направлению действием силы  . Эта работа отличается от работы статически нарастающей силы на собственных перемещениях, отсутствием коэффициента ½.
. Эта работа отличается от работы статически нарастающей силы на собственных перемещениях, отсутствием коэффициента ½.
Если силы  и
и  действуют в разное время, или приложены в разных состояниях системы, то работу, определяемую по формуле (6.10) называют возможной работой.
действуют в разное время, или приложены в разных состояниях системы, то работу, определяемую по формуле (6.10) называют возможной работой.
В сечениях изогнутой оси балки от действия силы  возникают изгибающие моменты
возникают изгибающие моменты 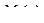 , а в сечениях изогнутой оси балки от действия силы
, а в сечениях изогнутой оси балки от действия силы  возникают изгибающие моменты
возникают изгибающие моменты 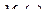 , которые вызывают угловые перемещения по направлению
, которые вызывают угловые перемещения по направлению 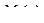 . Эти перемещения относятся к элементу балки длиной
. Эти перемещения относятся к элементу балки длиной 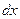 и определяются по формуле:
и определяются по формуле:
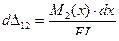
На этом перемещении изгибающий момент 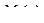 совершает элементарную дополнительную (возможную) работу равную произведению этого момента на перемещение, вызванное действием момента
совершает элементарную дополнительную (возможную) работу равную произведению этого момента на перемещение, вызванное действием момента  :
:
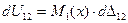 или
или 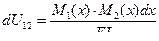 .
.
Проинтегрировав последнее выражение по всем участкам и сложив результаты интегрирования, получим формулу дополнительной (возможной ) потенциальной энергии.
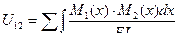 (6.11)
(6.11)
6.6. Теорема о взаимности возможных работ внешних сил (теорема Бетти).
Рассмотрим два состояния упругой балки, загруженные двумя обобщенными силами  и
и  . В состоянии 1 (оис.6.5,а) сначала приложим силу
. В состоянии 1 (оис.6.5,а) сначала приложим силу  , а после достижения конечного значения этой силы, приложим силу
, а после достижения конечного значения этой силы, приложим силу  . В состоянии 2 наоборот, сначала приложим силу
. В состоянии 2 наоборот, сначала приложим силу  , а после достижения конечного значения этой силы, приложим силу
, а после достижения конечного значения этой силы, приложим силу  (рис.6.5,б). На рисунках показаны силы и перемещения по направлению этих сил.
(рис.6.5,б). На рисунках показаны силы и перемещения по направлению этих сил.
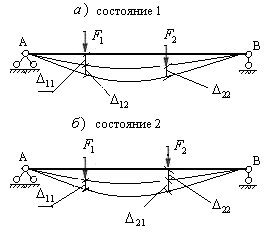
Рис.6.5
Определим полную работу внешних сил в двух состояниях:
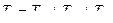 , или
, или 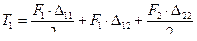 (6.12)
(6.12)
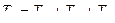 , или
, или 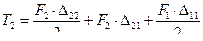 (6.13)
(6.13)
Приравняем правые части выражений (6.12) и (6.13) и сократим равные величины. В результате получим:
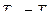 , или
, или  (6.14)
(6.14)
Таким образом, возможная работа силы  на упругом перемещении по её направлению, вызванном силой
на упругом перемещении по её направлению, вызванном силой  равна возможной работе силы
равна возможной работе силы  на упругом перемещении по её направлению, вызванном силой
на упругом перемещении по её направлению, вызванном силой  .
.
6.7. Теорема о взаимности возможных работ внутренних усилий.
Воспользуемся законом сохранения энергии в двух состояниях упругой балки, рассмотренных в предыдущем параграфе. Полная работа внешних сил и внутренних усилий в каждом состоянии упругой балки равна их сумме и не зависит от порядка загружения балки, т.е.:
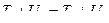 , (6.15)
, (6.15)
или
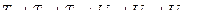
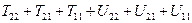
Исключим из последнего равенства одинаковые величины, получим:
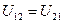 (6.16)
(6.16)
Таким образом, возможная работа внутренних усилий первого состояния на упругих перемещениях по их направлениям, вызванных усилиями второго состояния равна возможной работе внутренних усилий второго состояния на упругих перемещениях по их направлениям, вызванных усилиями первого состояния.
Возможная работа внутренних усилий балочных и рамных систем вычисляется по формуле (6.11), а возможная работа внутренних усилий в стержнях ферм по следующей формуле:
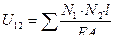 (6.17)
(6.17)
Примечание: Свойством взаимности обладают работы внешних сил и внутренних усилий каждого состояния упругой системы, т.е.:
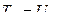 (6.18)
(6.18)
6.8. Теорема о взаимности перемещений (теорема Максвелла).
На основании теоремы о взаимности работ внешних сил имеем:
 ,
,
Если принять равными обобщенные силы 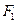 и
и  , то получим равенство перемещений:
, то получим равенство перемещений:
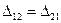 (6.19)
(6.19)
Таким образом, упругое перемещение по направлению первой обобщенной силы, вызванное действием второй обобщенной силы равно упругому перемещению по направлению второй обобщенной силы, вызванному действием первой обобщенной силы.
Это и есть теорема Максвелла о взаимности перемещений.
Следствие из теоремы: Если силы 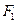 и
и  равны единице (единичные силы), то имеет место свойство взаимности единичных перемещений:
равны единице (единичные силы), то имеет место свойство взаимности единичных перемещений:
 (6.20)
(6.20)
6.9. Универсальная формула Мора для определения упругих перемещений.
Рассмотрим два состояния упругой балки. В состоянии 1 балка загружена произвольными силами, а в состоянии 2 она загружена только одной единичной силой 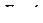 (рис.6.6).
(рис.6.6).
В первом состоянии возникает упругое перемещение 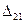 по направлению единичной силы второго состояния, любом поперечном сечении возникают внутренние усилия
по направлению единичной силы второго состояния, любом поперечном сечении возникают внутренние усилия 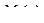 ,
, 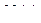 ,
,  .
.
В любом поперечном сечении второго состояния возникают единичные внутренние усилия  ,
, 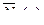 ,
,  .
.

Рис.6.6
Согласно теореме о взаимности работ внешних сил и внутренних усилий второго состояния на соответствующих им перемещениях первого состояния, имеем:
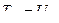 ,
,
но  ,
,
а 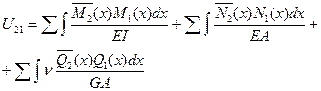
Тогда:
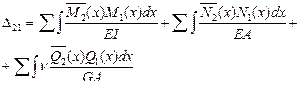 (6.21)
(6.21)
При вычислении перемещений в балочных или рамных стержневых системах по формуле Мора (6.21) учитывают влияние только изгибающих моментов, т.е. используют только первое слагаемое правой части этой формулы.
При вычислении перемещений в фермах по формуле Мора (6.21) учитывают влияние только продольных сил, т.е. используют только второе слагаемое правой части этой формулы.
Пример 6.1 Вычислить угол поворота правого опорного сечения однопролетной балки на двух шарнирных опорах, загруженной равномерно распределенной нагрузкой и имеющей постоянную жесткость 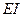 по всей длине (рис.6.7).
по всей длине (рис.6.7).
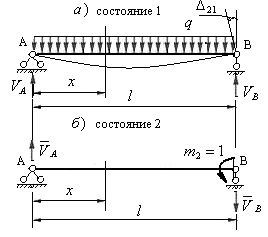
Рис.6.7
Решение: 1) Заданную балку принимаем как состояние 1, вычисляем реакции опор и составляем уравнение изгибающих моментов в произвольном сечении.
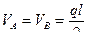 ,
, 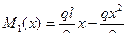
2) Создаем возможное состояние 2 путем загружения той же балки одним сосредоточенным единичным моментом  . Определяем реакции опор и составляем уравнение изгибающих моментов в этом состоянии.
. Определяем реакции опор и составляем уравнение изгибающих моментов в этом состоянии.
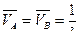 (направления реакций показаны на рис.6.7,б),
(направления реакций показаны на рис.6.7,б), 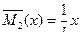
Уравнения изгибающих моментов в двух состояниях справедливы в интервале изменения переменной 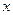 от нуля до
от нуля до 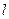 . Следовательно, имеем один участок интегрирования.
. Следовательно, имеем один участок интегрирования.
3) Вычисляем угол поворота правого опорного сечения балки, используя первое слагаемое правой части формулы Мора.
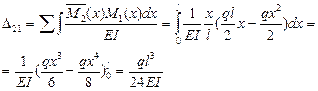
6.10. Вычисление перемещений перемножением эпюр изгибающих моментов (правило Верещагина).
Обозначим букой 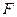 заданное состояние стержневой системы и буквой
заданное состояние стержневой системы и буквой 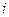 возможное единичное состояние той же системы. Тогда вычисление упругих перемещений по формуле Мора будет связано с вычислением интеграла:
возможное единичное состояние той же системы. Тогда вычисление упругих перемещений по формуле Мора будет связано с вычислением интеграла:
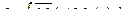 (6.22)
(6.22)
Рассмотрим случай, когда эпюра изгибающих моментов на некотором участке заданного состояния имеет произвольное очертание (не прямолинейна), а единичная эпюра изгибающих моментов на том же участке возможного состояния прямолинейна (рис.6.8).
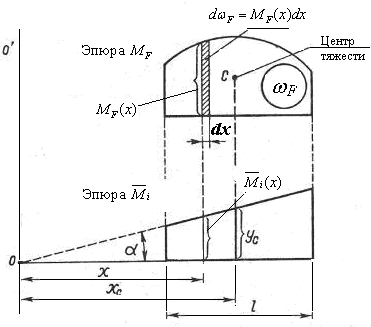
Рис.6.8
Выделим элементарную полоску эпюры 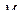 шириной
шириной 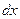 , тогда её площадь будет равна
, тогда её площадь будет равна 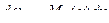 .
.
Ордината единичной эпюры изгибающих моментов под полоской равна 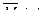 . Выразим эту ординату через угол наклона эпюры к горизонтальной прямой:
. Выразим эту ординату через угол наклона эпюры к горизонтальной прямой:
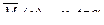 , тогда интеграл (6.22) преобразуется к виду:
, тогда интеграл (6.22) преобразуется к виду:
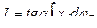 (6.23)
(6.23)
Легко заметить, что интеграл выражения (6.23) равен статическому моменту площади эпюры 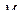 относительно вертикальной оси, проходящей через точку О. Из теоретической механики известно, что статический момент площади относительно оси равен произведению этой площади на расстояние от её центра тяжести до оси.
относительно вертикальной оси, проходящей через точку О. Из теоретической механики известно, что статический момент площади относительно оси равен произведению этой площади на расстояние от её центра тяжести до оси.
Обозначим площадь эпюры 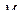 через
через  , а расстояние от её центра тяжести до оси, через
, а расстояние от её центра тяжести до оси, через  , тогда получим:
, тогда получим:
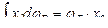 (6.24)
(6.24)
В результате интеграл (6.23) преобразуется к виду:
 (6.25)
(6.25)
Таким образом, интеграл (6.22) на любом участке, где одна из двух эпюр изгибающих моментов прямолинейная, равен произведению площади не прямолинейной эпюры на ординату прямолинейной эпюры, взятую под центром тяжести первой.
Для стержневой системы, имеющей несколько участков, упругое перемещение определяется по формуле:
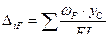 (6.26)
(6.26)
Правило знаков: Если перемножаемые эпюры изгибающих моментов в двух состояниях расположены по одну сторону от осей системы, то результат перемножения имеет знак плюс. Если же перемножаемые эпюры расположены по разные стороны от осей системы, то результат перемножения имеет знак минус.
Примечания: 1) Перемещение, вычисленное по правилу Верещагина (по формуле 6.26) может иметь знак плюс или минус. Направление перемещения определяется направлением единичной силы возможного состояния. Следовательно, если перемещение имеет знак плюс, то оно имеет то же направление, что и единичная сила. Если же перемещение имеет знак минус, то оно направлено противоположно единичной силе.
2) При перемножении двух прямолинейных эпюр можно вычислять площади любой из них на отдельных участках, а ординаты под их центрами тяжести принимать из другой эпюры.
Пример 6.2 Определить прогиб по середине пролета балки постоянной жесткости 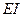 , загруженной равномерно распределенной нагрузкой (рис.6.9).
, загруженной равномерно распределенной нагрузкой (рис.6.9).
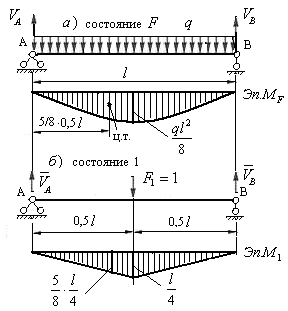
Рис.6.9
Решение: 1) Заданную состояние балки обозначим 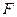 , вычислим реакции опор, составим уравнение изгибающих моментов в произвольном сечении и построим эпюру изгибающих моментов
, вычислим реакции опор, составим уравнение изгибающих моментов в произвольном сечении и построим эпюру изгибающих моментов 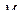 :
:
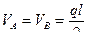 ,
, 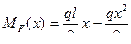
Эпюра 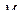 ограничена квадратичной параболой, имеющей нулевые ординаты под опорами и максимальную ординату по середине пролета балки. Эта ордината равна:
ограничена квадратичной параболой, имеющей нулевые ординаты под опорами и максимальную ординату по середине пролета балки. Эта ордината равна:

2) Создаем возможное состояние 1 путем загружения той же балки одной единичной сосредоточенной силой  , вычисляем реакции опор и строим единичную эпюру изгибающих моментов
, вычисляем реакции опор и строим единичную эпюру изгибающих моментов 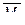 .
. 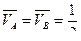 (направления реакций показаны на рис.6.9,б),
(направления реакций показаны на рис.6.9,б), 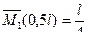
3) Вычисляем прогиб балки в направлении силы  , перемножая эпюры изгибающих моментов в двух состояниях по правилу Верещагина. Эпюра
, перемножая эпюры изгибающих моментов в двух состояниях по правилу Верещагина. Эпюра 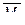 прямолинейна на двух участках балки, симметричных относительно середины пролета. На тех же участках эпюра
прямолинейна на двух участках балки, симметричных относительно середины пролета. На тех же участках эпюра 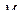 криволинейна и симметрична. Поэтому перемножаем эпюры на левом участке и результат удваиваем., т.е.:
криволинейна и симметрична. Поэтому перемножаем эпюры на левом участке и результат удваиваем., т.е.:
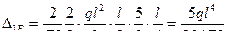
Примечание: Площадь выпуклого параболического сегмента равна 2/3 произведения высоты на длину, центр тяжести отстоит от нулевой вершины на расстоянии 5/8 длины участка.
Вопросы для самоконтроля полученных знаний.
1. Для каких целей необходимо вычислять перемещения?
2. Как формулируется принцип возможных перемещений для упругих систем?
3. Что такое возможное перемещение?
4. Как зависят перемещения от нагрузки в линейно деформируемых системах?
5. Как определяется действительная работа внешних сил?
6. В чем различие между действительной и возможной работой?
7. Как определяется возможная работа внутренних сил?
8. Чем объясняется наличие знака «минус» в выражении возможной работы внутренних сил?
9. Как получить действительную работу внутренних сил?
10. Как определяется потенциальная энергия деформации системы?
11. Как зависит потенциальная энергия от нагрузки? От перемещений?
12. Каковы свойства потенциальной энергии?
13. Как формулируется и доказывается теорема Бетти о взаимности работ?
14. Сформулируйте и докажите теорему Максвелла о взаимности перемещений; теорему о взаимности реакций; теорему о взаимности перемещений и реакций.
15. Как записывается формула Мора?
16. Какие два состояния системы необходимо рассматривать при определении перемещений по формуле Мора?
17. Когда можно применять правило Верещагина? Формулу Симпсона?
Глава 7. Расчет статически неопределимых рам методом сил
7.1. Краткая характеристика статически неопределимых рам. Степень статической неопределимости.
Рамой называют систему, состоящую из прямолинейных стержней, объединенных между собой в узлах жестко или шарнирно и присоединенных к неподвижным телам при помощи опорных устройств. Плоские рамы могут иметь защемляющие, шарнирно неподвижные и шарнирно подвижные опоры. Вертикальные стержни рамы называют стойками, а горизонтальные - ригелями. В отдельных случаях рама может иметь наклонные стойки или наклонные ригели.
Если реакции опор рамы могут быть определены из уравнений равновесия статики, то рама является статически определимой.
Если же реакции опор рамы не могут быть определены из уравнений равновесия статики, то рама является статически неопределимой.
Разность между числом неизвестных усилий, возникающих в связях статически неопределимой рамы от действия заданных внешних нагрузок и числом уравнений равновесия, которые можно составить для этой рамы по методу равновесия дисков, называется степенью статической неопределимости рамы. Степень статической неопределимости обозначается буквой Л и выражает собой количество «лишних» связей статически неопределимой рамы, т.е. количество связей, для определения которых недостает уравнений равновесия.
Любая статически неопределимая плоская рама имеет определенное число дисков, объединенных между собой цилиндрическими шарнирами и прикрепленных к неподвижным телам с помощью опорных связей. Обозначим через Д - число простых дисков рамы (дисков, которые не содержат замкнутых контуров), через Шн - число простых цилиндрических шарниров (шарниров, которые объединяют между собой только два диска) и через Со- число простых одиночных опорных связей заданной рамы (защемляющая опора плоской рамы имеет три простые связи, шарнирно неподвижная опора имеет две простые связи и шарнирно подвижная опора имеет одну простую связь).
Тогда степень статической неопределимости плоской рамы будет равна:
Л = 2Шн + Со – 3Д (7.1)
Примечания: 1) Если цилиндрический шарнир объединяет в одной точке несколько дисков, то он является составным или кратным, т.е. эквивалентным нескольким простым шарнирам. Кратность составного шарнира равна количеству объединяемых дисков без одного, т.е.
Кш = Д -1 (7.2)
2) Если диск содержат один замкнутый контур, то он являются три раза статически неопределимым. Рама может иметь несколько замкнутых контуров, тогда при определении степени статической неопределимости рамы необходимо в правой части формулы (7.1) прибавить утроенное число замкнутых контуров рамы К или уменьшить число дисков на число замкнутых контуров. В этом случае степень статической неопределимости плоской рамы с замкнутыми контурами будет определяться по следующей формуле:
Л = 2Шн + Со – 3(Д – К) (7.3)
3) Число простых одиночных опорных связей Со определяется в зависимости от принятых типов опорных устройств рамы.
Рассмотрим три расчетные схемы статически неопределимых рам и установим их степень статической неопределимости.
Двухэтажная однопролетная рама 1 (рис.7.1,а) состоит из двух дисков (Д=2), двух простых цилиндрических шарниров (Шн=2) и пяти простых одиночных опорных связей (Со=5). Применяя формулу (6.1) найдем:
Л = 2∙2 + 5 – 3∙2 = 3 , следовательно, рама 1 три раза статически неопределима, т.е. имеет три «лишние» связи.
Одноэтажная двухпролетная рама 2 (рис.7.1,б) состоит из трех дисков, двух простых цилиндрических шарниров (один двукратный шарнир) и 9 простых одиночных опорных связей (три защемляющие опоры). Тогда, по формуле (7.1) находим:
Л = 2∙2 + 9 – 3∙3 = 4, следовательно, рама 2 имеет четыре «лишние» связи, т.е. четыре раза статически неопределима.
Двухэтажная однопролетная рама 3 (рис.7.1,в) состоит из одного диска, имеющего один замкнутый контур, и пяти простых опорных связей. Тогда по формуле (7.3) найдем:
Л = 5 – 3(1-1) = 5, следовательно, рама 3 имеет пять «лишних» связей и является пять раз статически неопределимой..
Напомним, что для определения числа дисков необходимо отбросить мысленно все опорные и все шарнирные связи. Если, при этом, рама разделится (распадется) на отдельные части, то каждая из них будет являться отдельным диском. Если рама не делится на части, то она состоит из одного диска.
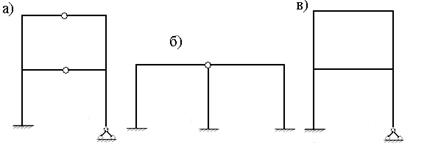
Рис.7.1
Любая связь рамы имеет две характеристики: статическую и кинематическую. Статическая характеристика определяет величину и направление реакции рассматриваемой связи, а кинематическая характеристика величину и направление перемещения, которое допускает данная связь.
Статическая и кинематическая характеристики связей находятся в определенной математической зависимости, устанавливаемой физическим законом деформирования упругих систем. Поэтому расчет рамы всегда состоит в определении статических и кинематических характеристик.
Если за независимые неизвестные принимают усилия в связях рамы, то метод расчета называют методом сил. Если же за независимые неизвестные принимают кинематические характеристики связей, то метод расчета называют методом перемещений.
В настоящей главе рассматривается метод сил, являющийся одним из основных методов расчета рам, а также других стержневых систем.
7.2. Основная система метода сил.
При использовании метода сил за неизвестные принимаются усилия в тех связях заданной рамы, которые приняты «лишними». За лишние связи могут приниматься любые связи рамы при условии, что после их освобождения полученная система будет статически определимой, геометрически неизменяемой и неподвижной. Такая система называется основной системой метода сил (ОС). Для любой статически неопределимой рамы можно образовать несколько вариантов основной системы. Чем выше степень статической неопределимости рамы, тем больше вариантов основной системы возможно образовать.
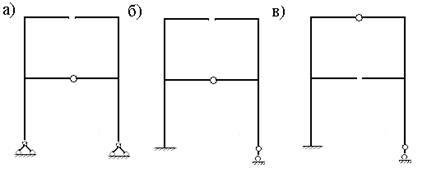
Рис.7.2
На рис.6.2 показаны три варианта основной системы метода сил, которые могут быть приняты при расчете рамы, представленной на рис.7.1,а. Они образуются освобождением трех связей заданной рамы.
Первый вариант ОС образуем путем удаления одного шарнира (удобнее шарнира второго этажа заданной рамы) и замены защемляющей опоры шарнирно неподвижной опорой (рис.7.2,а). Второй вариант ОС можно образовать путем удаления того же шарнира и замены правой шарнирно неподвижной опоры шарнирно подвижной опорой (рис.7.2,б). В третьем варианте ОС удаляем шарнир первого этажа и заменяем защемляющую опору шарнирно неподвижной опорой (рис.7.2,в).
Для расчета рамы можно использовать любой вариант основной системы, но удачный её выбор позволяет упростить решение задачи. Если удается образовать основную систему, имеющую геометрическую и жесткостную симметрии, то достигается упрощение уравнений относительно неизвестных метода сил. Этим условиям удовлетворяет первый вариант ОС и его следует пронять для расчета заданной рамы.
Для образования основной системы метода сил при расчете рамы (рис.7.1,б) необходимо удалить четыре связи.
В первом варианте можно освободить связи двукратного шарнира.
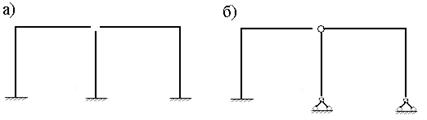
Рис.7.3
В результате ОС метода сил будет состоять из трех дисков с защемляющими опорами (оис.7.3,а). Во втором варианте освобождаем связи одного шарнира и заменяем две защемляющие опоры шарнирно неподвижными опорами (рис.7.3,б).
Для образования основной системы метода сил при расчете рамы (рис.7.1,в) необходимо удалить пять связей. Три из них освобождаем, рассекая один из ригелей рамы (лучше верхний), одну связь освобождаем введением шарнира в сечение другого ригеля, и одну связь освобождаем на одной из опор. В результате получаем три варианта ОС, представленные на рис.7.2.
7.3. Эквивалентная система метода сил.
Если основную систему метода сил загрузить заданными нагрузками и неизвестными усилиями в освобожденных связях, то полученная система будет называться эквивалентной системой (ЭС). Неизвестные усилия в освобожденных связях обозначают буквой  независимо от того, является ли неизвестное усилие сосредоточенной силой или сосредоточенным моментом. Индекс усилия обозначает порядковый номер освобожденной связи.
независимо от того, является ли неизвестное усилие сосредоточенной силой или сосредоточенным моментом. Индекс усилия обозначает порядковый номер освобожденной связи.
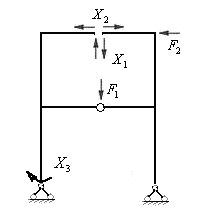
Рис.7.4
Образуем эквивалентную систему для рамы (рис.7.1,а), приняв для расчета первый вариант основной системы. Для этого загрузим ОС заданными нагрузками (например, двумя сосредоточенными силами 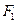 и
и  ) и тремя неизвестными усилиями, компенсирующими влияние удаленных связей заданной рамы. Усилия
) и тремя неизвестными усилиями, компенсирующими влияние удаленных связей заданной рамы. Усилия  и
и  , которые удаленный шарнир передает от одного диска к другому, прикладываем к разъединенным концам ригеля. Вертикальные силы
, которые удаленный шарнир передает от одного диска к другому, прикладываем к разъединенным концам ригеля. Вертикальные силы  являются поперечными силами в ригеле. Они равны по величине и противоположны по направлению. Горизонтальные силы
являются поперечными силами в ригеле. Они равны по величине и противоположны по направлению. Горизонтальные силы  являются продольными силами в ригеле и также равны по величине и противоположны по направлению. Усилие
являются продольными силами в ригеле и также равны по величине и противоположны по направлению. Усилие  , компенсирующее влияние освобожденной опорной связи, которая препятствовала повороту опорного сечения левой стойки рамы, является реактивным моментом. Его направляем по ходу часовой стрелки (или против часовой стрелки). В результате получаем эквивалентную систему, показанную на рис.7.4
, компенсирующее влияние освобожденной опорной связи, которая препятствовала повороту опорного сечения левой стойки рамы, является реактивным моментом. Его направляем по ходу часовой стрелки (или против часовой стрелки). В результате получаем эквивалентную систему, показанную на рис.7.4
В эквивалентной системе под действием всех нагрузок могут возникать перемещения по направлению реакций удаленных опор или взаимные перемещения разъединенных точек отдельных стержней, в которых освобождены внутренние связи рамы, по направлению их реакций. При некоторых определенных значениях неизвестных усилий в освобожденных связях, зависящих от характера и величины внешнего загружения рамы, а также от геометрических размеров стержней и величин их изгибных жесткостей, указанные перемещения обращаются в нуль.
Условия равенства нулю перемещений точек эквивалентной системы по направлению неизвестных усилий, компенсирующих влияние освобожденных связей заданной рамы, называются условиями эквивалентности или условиями неразрывности перемещений в точках, где освобождены связи. Число условий эквивалентности всегда равно степени статической неопределимости рамы или числу неизвестных сил сопротивления, компенсирующих влияние освобожденных связей заданной рамы. Для ЭС показанной на рис.7.4 должны выполняться три условия эквивалентности:

 (7.4)
(7.4)

7.4. Канонические уравнения метода сил.
Канонические уравнения метода сил вытекают из условий эквивалентности (7.4) при использовании принципа независимости действия нагрузок, приложенных к эквивалентной системе (ЭС).
Составим первое каноническое уравнение, используя условие эквивалентности  системы (рис.7.4).
системы (рис.7.4).
Под действием всех нагрузок, приложенных к эквивалентной системе, точки приложения сил  могут получить взаимное смещение в вертикальном направлении на величину
могут получить взаимное смещение в вертикальном направлении на величину 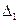 . Используя принцип независимости действия нагрузок, найдем:
. Используя принцип независимости действия нагрузок, найдем:
 (7.5)
(7.5)
Т.е. взаимное перемещение по направлению сил  в эквивалентной системе (из рисунка 7.4 следует, что это взаимное вертикальное перемещение) равно сумме взаимных перемещений по направлению силы
в эквивалентной системе (из рисунка 7.4 следует, что это взаимное вертикальное перемещение) равно сумме взаимных перемещений по направлению силы  , вызванных действием всех неизвестных усилий
, вызванных действием всех неизвестных усилий  ,
,  ,
,  и всех заданных внешних нагрузок. Перемещение по направлению любого неизвестного усилия не равного единице, равно произведению модуля этого усилия на единичное перемещение, т.е.
и всех заданных внешних нагрузок. Перемещение по направлению любого неизвестного усилия не равного единице, равно произведению модуля этого усилия на единичное перемещение, т.е.
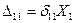 ,
,  ,
, 
Подставим эти значения в равенство (7,5 ) и приравняем к нулю 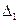 , в результате получим первое каноническое уравнение метода сил для рамы с тремя лишними связями.
, в результате получим первое каноническое уравнение метода сил для рамы с тремя лишними связями.
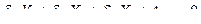
Используя аналогично два последующих условия эквивалентности (7.4), получим второе и третье канонические уравнения метода сил. Все три уравнения составляют систему канонических уравнений метода сил.
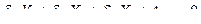
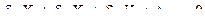 (7.6)
(7.6)
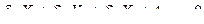
Любое каноническое уравнение метода сил является отрицанием наличия перемещения по направлению соответствующего неизвестного усилия в эквивалентной системе. В этом состоит физический смысл канонических уравнений метода сил.
В общем случае, когда заданная рама имеет n «лишних» связей, система канонических уравнений метода сил имеет вид:


 (7.7)
(7.7)
.……………………………………………
……………………………………………

7.5. Анализ коэффициентов и свободных членов канонические уравнения метода сил.
Коэффициенты канонических уравнений метода сил являются единичными перемещениями точек основной системы (ОС), где освобождены связи. Они возникают по направлению неизвестного усилия, индекс которого совпадает с первым индексом перемещения, от действия единичного значения неизвестного усилия, индекс которого совпадает со вторым индексом искомого перемещения. Так, например, коэффициент δ ik есть единичное перемещение в основной системе по направлению усилия Xi от действия усилия Xk=1.
Свободные члены канонических уравнений являются грузовыми перемещениями в основной системе по направлению неизвестных усилий, индексы которых совпадают с первыми индексами искомых перемещений.
Все коэффициенты канонических уравнений метода сил делятся на две группы: главные и побочные. Главные коэффициенты имеют одинаковые индексы и всегда имеют положительные значения. Они расположены по главной диагонали канонических уравнений (7.6) или (7.7).
Побочные коэффициенты имеют разные индексы и могут быть положительными, отрицательными или равными нулю. При этом побочные коэффициенты, расположенные симметрично главной диагонали обладают свойством взаимности, т.е. равны по величине и знаку на основании теоремы о взаимности возможных перемещений. Например, 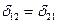 ,
, 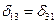 и т.д. Это свойство позволяет сократить количество коэффициентов, подлежащих определению. Например, система уравнений (7.6) девять неизвестных коэффициентов: три главных и шесть побочных. Вычислению подлежат главные коэффициенты и половина побочных, т.е. три. Всего необходимо вычислить шесть коэффициентов и три грузовые перемещения.
и т.д. Это свойство позволяет сократить количество коэффициентов, подлежащих определению. Например, система уравнений (7.6) девять неизвестных коэффициентов: три главных и шесть побочных. Вычислению подлежат главные коэффициенты и половина побочных, т.е. три. Всего необходимо вычислить шесть коэффициентов и три грузовые перемещения.
7.6. Способы вычисления коэффициентов и свободных членов канонические уравнения метода сил.
Все известные способы (методы) определения упругих перемещений могут быть использованы для вычисления коэффициентов и грузовых перемещений канонических уравнений метода сил. Основными из них являются: метод начальных параметров, метод упругих грузов, метод Мора-Максвелла, правило Верещагина.
Остановимся подробнее на использовании двух последних методов.
Метод Мора-Максвелла состоит в использовании универсальной формулы упругих перемещений стержневых систем. Например, при расчете балочных и рамных статически неопределимых стержневых систем, коэффициенты и грузовые перемещения вычисляются по формулам:
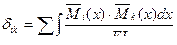 (7.8)
(7.8)
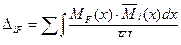 (7.9)
(7.9)
В этих формулах содержаться уравнения изгибающих моментов на каждом участке основной системы:
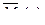 - уравнение изгибающих моментов на произвольном участке основной системы, загруженной силой
- уравнение изгибающих моментов на произвольном участке основной системы, загруженной силой 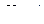 ;
;
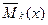 - уравнение изгибающих моментов на том же участке основной системы, загруженной силой
- уравнение изгибающих моментов на том же участке основной системы, загруженной силой 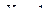 ;
;
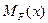 - уравнение изгибающих моментов на том же участке основной системы, загруженной всеми внешними нагрузками.
- уравнение изгибающих моментов на том же участке основной системы, загруженной всеми внешними нагрузками.
При расчете статически неопределимых рам рекомендуется вычислять коэффициенты и грузовые перемещения по правилу Верещагина путем перемножения эпюр изгибающих моментов, построенных в основной системе метода сил.
Для этого необходимо построить единичные и грузовую эпюры изгибающих моментов в основной системе. Если загрузить основную систему силой  , определить реакции опор, вычислить изгибающие моменты на концах каждого стержня, отложить их от оси стержня в сторону растянутой зоны и соединить прямыми линиями, то получим единичную эпюру
, определить реакции опор, вычислить изгибающие моменты на концах каждого стержня, отложить их от оси стержня в сторону растянутой зоны и соединить прямыми линиями, то получим единичную эпюру 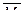 .
.
При вычислении изгибающих моментов в характерных сечениях стержней рамы необходимо придерживаться следующего порядка их рассмотрения:
- сначала рассматривают стержни от опор, реакции которых вычислены, к жестким узлам рамы;
- затем рассматривают консольные части стержней от их свободных концов к жестким узлам рамы;
- стержни рамы, объединяющие жесткие узлы, рассматривают в последнюю очередь.
При этом каждый жесткий узел рамы должен находиться в равновесии под действием узловых изгибающих моментов. Это свойство используется как для проверки правильности построения эпюр, так и для определения изгибающего момента в узловом сечении одного из стержней, если изгибающие моменты в узловых сечениях остальных стержней уже известны.
Аналогично осуществляют построение единичных эпюр изгибающих моментов 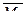 ,
, 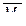 и
и
Для построения грузовой эпюры изгибающих моментов 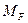 в основной системе метода сил следует загрузить эту систему заданными нагрузками, определить реакции опор, разделить раму на участки и вычислить изгибающие моменты на концах каждого из них. Если участок загружен распределенной нагрузкой, то необходимо дополнительно вычислить изгибающий момент посредине этого участка.
в основной системе метода сил следует загрузить эту систему заданными нагрузками, определить реакции опор, разделить раму на участки и вычислить изгибающие моменты на концах каждого из них. Если участок загружен распределенной нагрузкой, то необходимо дополнительно вычислить изгибающий момент посредине этого участка.
После построения единичных и грузовой эпюр изгибающих моментов в основной системе, вычисляют по правилу Верещагина коэффициенты и грузовые перемещения по формулам:
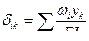 ,
, 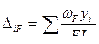 (7.10)
(7.10)
Где: ω i – площадь эпюры 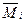 на произвольном участке;
на произвольном участке;
ωF - площадь эпюры 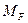 на произвольном участке;
на произвольном участке;
yi - ордината эпюры 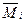 , взятая под центром тяжести эпюры
, взятая под центром тяжести эпюры 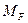 ;
;
yk - ордината эпюры 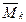 , взятая под центром тяжести эпюры
, взятая под центром тяжести эпюры 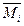 .
.
Учитывая, что единичные эпюры изгибающих моментов на каждом участке основной системы прямолинейные и чаще всего имеют форму треугольника или прямоугольника, коэффициенты канонических уравнений легко вычисляются. Грузовая эпюра изгибающих моментов может иметь криволинейное очертание на отдельных участках, которые несут распределенную нагрузку. Такая эпюра всегда может быть разделена на составные части, площади и положения центров тяжести которых, легко определяются.
Таким образом, всегда есть возможность вычислить единичные и грузовые перемещения по формулам (7.10).
7.7. Способы решения канонические уравнения метода сил.
Канонические уравнения метода сил являются линейными алгебраическими уравнениями с постоянными коэффициентами.
Решение системы канонических уравнений метода сил (7.6) или (7.7) можно получить методом последовательного исключения неизвестных (уравнивания коэффициентов при неизвестных), либо методом определителей (детерминантов).
При использовании первого метода каждое уравнение делят на коэффициент при одном из неизвестных усилий (например, на коэффициент при неизвестной силе 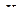 ), т.е. уравнивают коэффициенты при неизвестной силе
), т.е. уравнивают коэффициенты при неизвестной силе 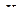 в каждом уравнении. Вычитая, затем, из первого уравнения второе, из второго уравнения третье и т.д., получаем новую систему уравнений, не содержащую неизвестной силы
в каждом уравнении. Вычитая, затем, из первого уравнения второе, из второго уравнения третье и т.д., получаем новую систему уравнений, не содержащую неизвестной силы 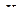 . Число уравнений новой системы будет на одно меньше числа уравнений исходной системы.
. Число уравнений новой системы будет на одно меньше числа уравнений исходной системы.
Аналогично исключают из уравнений неизвестные 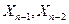 и так далее, пока не получим одно уравнение с одной неизвестной
и так далее, пока не получим одно уравнение с одной неизвестной  . Вычислив значение
. Вычислив значение  , вычисляют последовательно, обратным ходом, значения
, вычисляют последовательно, обратным ходом, значения  ,
, 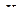 и т.д.
и т.д.
При этом рекомендуется осуществлять поэтапную проверку найденных значений искомых усилий. Усилие определяется из одного уравнения системы, а левые части остальных уравнений должны быть равными нулю при подстановке вычисленных усилий.
При использовании второго метода любое неизвестное усилие определяется отношением определителя неизвестного к определителю системы уравнений, т.е. по формуле:
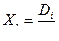 (7.11)
(7.11)
Определитель системы формируется из коэффициентов системы канонических уравнений. Число строк и число столбцов этого определителя равно числу канонических уравнений. При n неизвестных метода сил он имеет следующий вид:
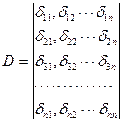 (7.12)
(7.12)
Определитель неизвестного формируется из определителя системы уравнений путем замены в нем столбца коэффициентов при определяемом неизвестном усилии свободными членами канонических уравнений, перенесенными в их правые части.
Например, определитель неизвестного усилия  имеет вид:
имеет вид:
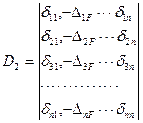 (7.13)
(7.13)
Метод определителей позволяет вычислить неизвестные усилия метода сил с использованием функции «МОПРЕД» программы Microsoft Excel. Для этого достаточно сформировать определитель системы и определители каждого неизвестного, применить указанную функцию и найти отношения матриц определителей по формуле (7.11).
7.8. Приемы определения внутренних усилий в заданной раме. Построение эпюр 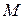 ,
,  ,
, 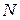 .
.
После вычисления неизвестных усилий в освобожденных «лишних» связях заданной рамы, можно определить изгибающие моменты, поперечные и продольные силы для каждого стержня и построить эпюры этих усилий.
При этом можно использовать два приёма:
1) Приём, основанный на применении метода сечений для построения эпюр внутренних усилий в статически определимых системах.
При его использовании необходимо основную систему метода сил загрузить заданными нагрузками и найденными из решения канонических уравнений значениями «лишних» неизвестных усилий в освобожденных связях. Разделить эту систему на участки, выбрать в пределах каждого из них произвольные сечения на переменных расстояниях от принятых начал координат, составить уравнения изгибающих моментов, поперечных и продольных сил и построить их графики, т.е эпюры соответствующих усилий.
Таким образом, определение внутренних усилий (изгибающих моментов, поперечных и продольных сил) и построение эпюр этих усилий осуществляется одновременно.
2) Приём, основанный на применении принципа независимости действия нагрузок.
Сначала осуществляется построение эпюры изгибающих моментов в заданной статически неопределимой раме.
Для этого следует построить исправленные эпюры изгибающих моментов в основной системе метода сил. Исправленные эпюры получают умножением ординат единичных эпюр на найденные значения соответствующих «лишних» неизвестных. Затем вычисляют ординаты эпюры изгибающих моментов в характерных сечениях заданной рамы. Они равны алгебраической сумме ординат грузовой эпюры и всех исправленных эпюр в тех же сечениях основной системы.
Таким образом, ординаты эпюры изгибающих моментов в произвольном сечении заданной рамы вычисляется по формуле:
 (7.14)
(7.14)
После построения эпюры изгибающих моментов вычисляют поперечные силы и строят эпюру 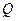 .
.
При вычислении поперечных сил на отдельных участках стержней заданной рамы следует использовать дифференциальные зависимости между изгибающим моментом, поперечной силой и интенсивностью внешней нагрузки. Из этих зависимостей следует, что на участках заданной рамы, где эпюра изгибающих моментов прямолинейная, поперечная сила имеет постоянное значение, равное тангенсу угла наклона эпюры изгибающих моментов к оси стержня, т.е.
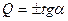 (7.15)
(7.15)
Верхний знак формулы (7.15) принимается в том случае, когда до совмещения с осью стержня эпюру изгибающих моментов следует повернуть против часовой стрелки. Нижний знак той же формулы принимается в том случае, когда до совмещения с осью стержня эпюру изгибающих моментов следует повернуть по часовой стрелке.
На рис.7.5 показан участок рамы 1-2, на котором эпюра изгибающих моментов прямолинейна. Вычислим поперечную силу на этом участке, используя формулу (7.15) и построим эпюру 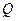 .
.
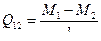 (7.16)
(7.16)
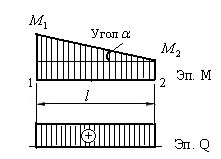
Рис.7.5
На участках рамы, загруженных равномерно распределенной нагрузкой, поперечные силы непрерывно меняются по длине, следуя линейной зависимости. Эпюра поперечных сил на таких участках может быть построена по двум ординатам, вычисленным для концевых сечений участка стержня по методу равновесия дисков. Для этого вырезают диск, загружают его распределенной нагрузкой 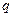 ,
,
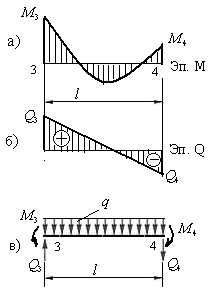
Рис.7.6
изгибающими моментами 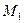 и
и 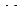 , величины и направления которых устанавливают по эпюре
, величины и направления которых устанавливают по эпюре 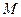 , а так же неизвестными поперечными силами в граничных сечениях участка. Эти силы направляют так, чтобы они вращали стержень по часовой стрелке. В этом случае поперечные силы будут иметь истинные знаки.
, а так же неизвестными поперечными силами в граничных сечениях участка. Эти силы направляют так, чтобы они вращали стержень по часовой стрелке. В этом случае поперечные силы будут иметь истинные знаки.
Используя два условия равновесия диска, составляют уравнения равновесия и вычисляют неизвестные поперечные силы, позволяющие построить эпюру 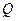 . На рис.7.6,а показана возможная эпюра изгибающих моментов на участке 3-4 рамы, загруженном распределенной нагрузкой
. На рис.7.6,а показана возможная эпюра изгибающих моментов на участке 3-4 рамы, загруженном распределенной нагрузкой 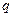 .
.
На рис.7.6,в показаны все нагрузки, действующие на участок 3-4 стержня рамы. Составим уравнения его равновесия:


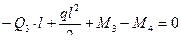

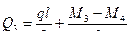 (7.17)
(7.17)


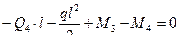

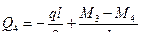 (7.18)
(7.18)
Продольные силы в стержнях заданной рамы определяются по методу равновесия узлов. Для этого сначала вырезают узлы, объединяющие два стержня, загружают их заданными сосредоточенными силами (если они приложены к узлам рамы), неизвестными продольными силами в рассеченных стержнях и поперечными силами в тех же стержнях.
Величины и направления поперечных сил устанавливаются по эпюре поперечных сил. Если поперечная сила имеет знак плюс, то её направляют так, чтобы она вращала узел по часовой стрелке. Если же поперечная сила имеет знак минус, то её направляют так, чтобы она вращала узел против часовой стрелки. Для каждого узла составляют два уравнения равновесия, используя рациональные условия (аналогично как при определении усилии в стержнях ферм).
Затем вырезают узлы рамы, объединяющие три стержня, усилие в одном из которых уже вычислено, загружают аналогично предыдущим узлам, составляют уравнения равновесия и вычисляют неизвестные продольные усилия.
При построении эпюры продольных усилий принято откладывать ординаты перпендикулярно к осям стержней в обе стороны от них. Таким образом, оси стержней будут являться средними линиями эпюры 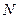 .
.
7.8. Проверки, осуществляемые при расчете рам методом сил.
В процессе расчета рам методом сил рекомендуется осуществлять следующие проверки:
а) построчную и суммарную проверки правильности вычисления коэффициентов и проверки грузовых перемещений канонических уравнений. Для этого следует построить суммарную единичную эпюру изгибающих моментов 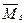 в основной системе путем алгебраического сложения ординат всех единичных эпюр. Затем перемножить по правилу Верещагина каждую единичную эпюру и грузовую эпюру на суммарную эпюру
в основной системе путем алгебраического сложения ординат всех единичных эпюр. Затем перемножить по правилу Верещагина каждую единичную эпюру и грузовую эпюру на суммарную эпюру 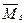 , а также суммарную эпюру изгибающих моментов саму на себя.
, а также суммарную эпюру изгибающих моментов саму на себя.
Результат перемножения эпюры 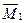 на эпюру
на эпюру 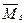 должен быть равным сумме всех коэффициентов первого канонического уравнения, т.е.
должен быть равным сумме всех коэффициентов первого канонического уравнения, т.е.
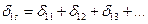 ;
;
Результат перемножения эпюры 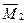 на эпюру
на эпюру 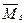 должен быть равным сумме всех коэффициентов второго канонического уравнения, т.е.
должен быть равным сумме всех коэффициентов второго канонического уравнения, т.е.
 ; и т.д.
; и т.д.
Результат перемножения эпюры 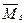 на ту же эпюру
на ту же эпюру 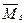 должен быть равным сумме всех коэффициентов системы канонических уравнений, т.е.
должен быть равным сумме всех коэффициентов системы канонических уравнений, т.е.

В скобках последнего равенства содержится сумма всех побочных коэффициентов, расположенных по одну сторону от главной диагонали системы уравнений.
Результат перемножения грузовой эпюры 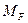 на эпюру
на эпюру 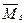 должен быть равным сумме свободных членов всех канонических уравнений, т.е.
должен быть равным сумме свободных членов всех канонических уравнений, т.е.

б) Проверка правильности решения системы канонических уравнений.
Если вычисленные значения усилий в освобожденных связях подставить в исходные канонические уравнения, то они должны обратиться в тождества  .
.
в) Проверки правильности построения эпюры изгибающих моментов: статическую и деформационную.
Статическая проверка состоит в том, что сумма изгибающих моментов в жестких узлах рамы должна быть равной нулю. В методе сил эта проверка является формальной, так как жесткие узлы рамы на единичных эпюрах и грузовой эпюре в основной системе, всегда находятся в равновесии.
Деформационная проверка состоит в том, что перемещение в заданной раме по направлению любой освобожденной связи должно быть равным нулю.
Для определения перемещения необходимо построить одну из единичных эпюр в новом варианте основной системы и перемножить её по правилу Верещагина на эпюру изгибающих моментов в заданной раме. Результат перемножения должен быть равным нулю (или близким к нулю).
г) Проверка равновесия заданной рамы в целом. Для выполнения этой проверки необходимо заданную раму освободить от всех опорных связей и загрузить заданными нагрузками и реакциями опорных связей. Величины и направления этих реакций легко установить по эпюрам изгибающих моментов, поперечных сил и продольных сил в заданной раме.
Загруженная таким образом рама должна удовлетворять трем условиям равновесия:
 ;
;  ;
;  .
.
Уравнения равновесия, составленные из этих условий, должны обратиться в тождества  .
.
Примеры расчета статически неопределимых рам методом сил
Пример 7.1: для рамы с заданными размерами и нагрузками (рис.2) требуется:
а) построить эпюры изгибающих моментов, поперечных и продольных сил;
б) проверить правильность построенных эпюр.
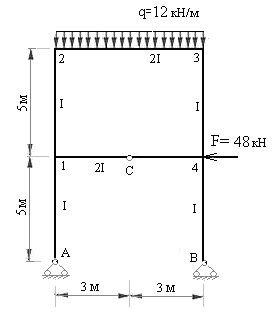
Рис.7.7
Последовательность решение задачи:
1) Устанавливаем степень статической неопределимости рамы по формуле: 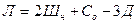 . Для заданной рамы имеем:
. Для заданной рамы имеем: 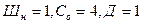 , тогда
, тогда 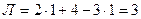 , т.е. рама три раза статически неопределима.
, т.е. рама три раза статически неопределима.
2) Выбираем основную систему метода сил путем освобождения трех лишних связей. За лишние связи можно принимать любые связи заданной рамы при условии, что после их освобождения (удаления) основная система будет статически определимой и неподвижной на плоскости.
Для любой статически неопределимой рамы можно образовать несколько вариантов основной системы. Чем выше степень статической неопределимости рамы, тем больше вариантов основной системы возможно предложить. На рисунках 7.8,а; 7.8,б; 7.8,в; 7.8,г показаны четыре варианта основной системы, которые могут быть приняты при расчете заданной рамы методом сил.
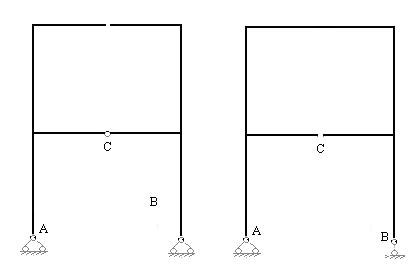
Рис.7.8,а Рис.7.8,б
Первый вариант основной системы (рис.7.8,а) образуем рассечением ригеля второго этажа заданной рамы (рассечь ригель можно в любом месте, как посредине пролета, так и вблизи одного из жестких узлов). Рассекая стержень на две части, освобождаем три связи:
- связь, препятствующую взаимному горизонтальному перемещению разъединенных частей стержня;
- связь, препятствующую взаимному вертикальному перемещению разъединенных частей стержня;
- связь, препятствующую взаимному повороту торцов, проведенного поперечного сечения стержня.
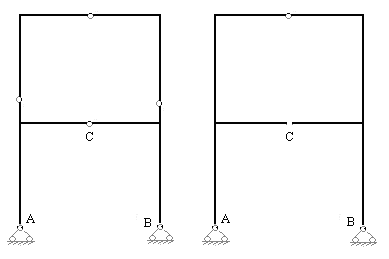
Рис.7.8.в Рис.7.8,г
Второй вариант основной системы (рис.7.8,б) выбираем путем удаления связей шарнира С заданной рамы (шарнир имеет две связи) и одной опорной связи на горизонтальное перемещение.
Третий вариант основной системы (рис.7.8,в) образуем введением трех цилиндрических шарниров в сечения ригеля и стоек второго этажа заданной рамы. Напомним, что введением шарнира в произвольное сечение стержня освобождается одна связь на взаимное угловое перемещение поперечных сечений, объединяемых шарниром.
Четвертый вариант основной системы (рис.7.8,г) образуем освобождением двух связей шарнира С и введение шарнира в среднее сечение ригеля второго этажа заданной рамы.
Примечание: при образовании основной системы вводить шарниры или рассекать стержни можно в произвольных местах. Однако, если заданная рама имеет ось геометрической и жесткостной симметрий, то упрощение расчета будет достигнуто при выборе симметричной основной системы. Все четыре варианта основной системы выбраны симметричными относительно вертикальной оси, проходящей через шарнир С заданной рамы.
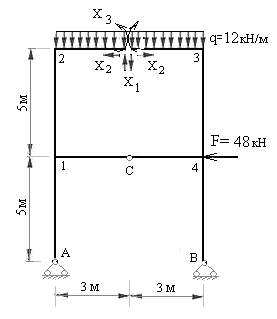
Рис.7.9
Принимаем для расчета рамы первый вариант основной системы (рис.7.8,а).
3) Образуем эквивалентную систему. Для этого основную систему загружаем заданными нагрузками и неизвестными усилиями 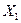 ,
,  и
и  , которые компенсируют действие на раму освобожденных связей в поперечном сечении ригеля второго этажа (рис.7.9).
, которые компенсируют действие на раму освобожденных связей в поперечном сечении ригеля второго этажа (рис.7.9).
4) Записываем систему канонических уравнений метода сил:
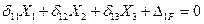
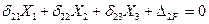 (7.19)
(7.19)
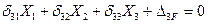
5) Строим единичные эпюры, а также грузовую эпюру изгибающих моментов в основной системе метода сил (рис.7.10,7.11, 7.12 и 7.13).
Для построения эпюр изгибающих моментов необходимо:
- определить реакции опор (величины и направления этих реакций от каждого вида нагрузки определяются из условий равновесия рамы в целом и отдельных дисков);
- вычислить изгибающие моменты в характерных сечениях каждого стержня;
- отложить их от оси каждого стержня в сторону растянутой зоны и соединить прямыми или кривыми линиями.
На рисунках 7.10-7.13 показаны направления и величины реакций опор и построены единичные эпюры и грузовая эпюра изгибающих моментов. Предлагаем изучающим курс составить необходимые уравнения равновесия и проверить найденные значения реакций и их направления.
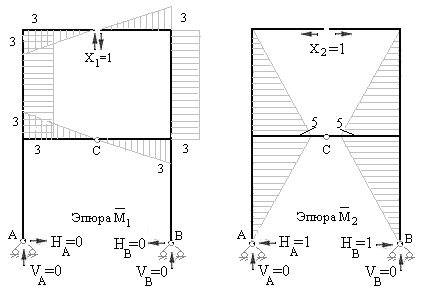
Рис.7.10 Рис.7.11
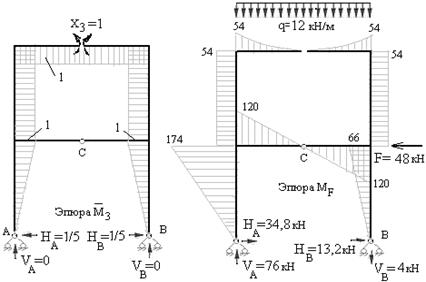
Рис.7.12 Рис.7.13
6) Определяем коэффициенты и грузовые перемещения канонических уравнений метода сил, пользуясь правилом Верещагина. Напомним, что перемножение эпюр изгибающих моментов осуществляется на каждом участке рамы, в пределах которого одна из двух перемножаемых эпюр прямолинейна, а вторая может иметь произвольное очертание и может быть разделена на части, площади и положения центров тяжести которых, легко определяются.
Единичные эпюры изгибающих моментов всегда имеют прямолинейное очертание в пределах отдельных стержней рамы. Поэтому коэффициенты канонических уравнений легко вычисляются по правилу Верещагина.
Вычислим, к примеру, коэффициент δ11. Для этого необходимо перемножить эпюру 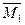 саму на себя, т.е. на каждом участке вычислить площадь эпюры, найти её ординату под собственным центром тяжести, перемножить эти величины и разделить на жесткость рассматриваемого участка рамы. Результаты перемножения на каждом участке алгебраически сложить.
саму на себя, т.е. на каждом участке вычислить площадь эпюры, найти её ординату под собственным центром тяжести, перемножить эти величины и разделить на жесткость рассматриваемого участка рамы. Результаты перемножения на каждом участке алгебраически сложить.
Как видно из рисунка 7.10 эпюра 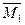 состоит из четырех одинаковых треугольников (жесткость рамы на этих участках также одинакова и равна 2EI) и двух одинаковых прямоугольников (жесткость рамы на этих участках также одинакова и равна EI). Тогда, применяя правило Верещагина, найдем:
состоит из четырех одинаковых треугольников (жесткость рамы на этих участках также одинакова и равна 2EI) и двух одинаковых прямоугольников (жесткость рамы на этих участках также одинакова и равна EI). Тогда, применяя правило Верещагина, найдем:
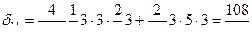 ;
;
Перемножая аналогично эпюры 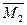 и
и 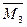 , найдем главные коэффициенты δ22 и δ33:
, найдем главные коэффициенты δ22 и δ33:
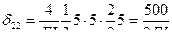 ;
;
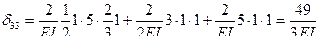 .
.
Необходимо помнить, что главные коэффициенты канонических уравнений всегда имеют положительные значения, так как площади и ординаты перемножаемых эпюр имеют один и тот же знак.
Вычисляем побочные коэффициенты канонических уравнений. Для этого перемножаем по правилу Верещагина единичные эпюры, имеющие разные индексы. Например, коэффициенты δ12=δ21 определяем перемножением единичных эпюр: 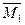 и
и 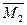 . Побочные коэффициенты могут иметь положительные, отрицательные или нулевые значения. Анализируя указанные эпюры, устанавливаем, что их перемножение следует выполнить на двух верхних стойках рамы.
. Побочные коэффициенты могут иметь положительные, отрицательные или нулевые значения. Анализируя указанные эпюры, устанавливаем, что их перемножение следует выполнить на двух верхних стойках рамы.
На левой стойке эпюры 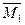 и
и 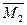 расположены по одну сторону от оси (справа), а на правой стойке эти эпюры расположены по разные стороны от её оси. Результат перемножения эпюр
расположены по одну сторону от оси (справа), а на правой стойке эти эпюры расположены по разные стороны от её оси. Результат перемножения эпюр 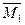 и
и 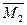 по правилу Верещагина на левой стойке будет иметь знак плюс, а результат перемножения этих эпюр на правой стойке будет иметь такую же величину и знак минус. Алгебраическая сумма указанных результатов перемножения будет равной нулю.
по правилу Верещагина на левой стойке будет иметь знак плюс, а результат перемножения этих эпюр на правой стойке будет иметь такую же величину и знак минус. Алгебраическая сумма указанных результатов перемножения будет равной нулю.
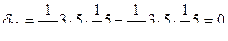
Следовательно, единичные перемещения 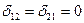 .
.
Примечание: Эпюра 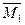 имеет косую симметрию относительно вертикальной оси, проведенной через середины ригелей рамы, а эпюра
имеет косую симметрию относительно вертикальной оси, проведенной через середины ригелей рамы, а эпюра 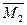 является симметричной относительно той же оси. Результат перемножения таких эпюр всегда равен нулю.
является симметричной относительно той же оси. Результат перемножения таких эпюр всегда равен нулю.
Напомним, что результат перемножения двух эпюр на любом участке имеет положительный знак, если они расположены с одной стороны от оси стержня и отрицательный знак, если они расположены по разные стороны от оси стержня.
Эпюра 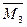 является симметричной, аналогично эпюре
является симметричной, аналогично эпюре 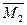 . Поэтому результат перемножения её на эпюру
. Поэтому результат перемножения её на эпюру 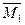 будет равным нулю, т.е.
будет равным нулю, т.е.  .
.
Вычислим побочные коэффициенты δ23=δ32, перемножая единичные эпюры 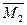 и
и 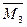 :
:
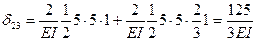
Определяем грузовые перемещения, перемножением грузовой эпюры на каждую из единичных эпюр. При этом используем свойство прямой и косой симметрии эпюр на отдельных участках.
Перемножаем эпюру 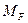 на эпюру
на эпюру 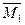 в пределах нижнего ригеля:
в пределах нижнего ригеля:
 ;
;
Перемножаем эпюру 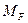 на эпюру
на эпюру 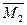 на всех стойках:
на всех стойках:
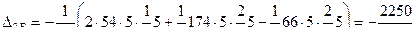 .
.
Перемножаем эпюру 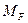 на эпюру
на эпюру 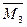 на всех стойках и верхнем ригеле:
на всех стойках и верхнем ригеле:
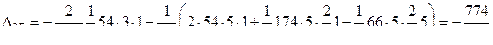 .
.
7) Определяем значения неизвестных усилий в освобожденных связях заданной рамы из решения канонических уравнений:
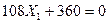
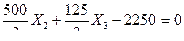 (7.20)
(7.20)
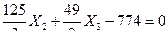
Из первого уравнения системы (7.20) находим 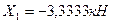
Из решения второго и третьего уравнений системы (7.20), находим:
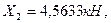
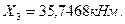
.
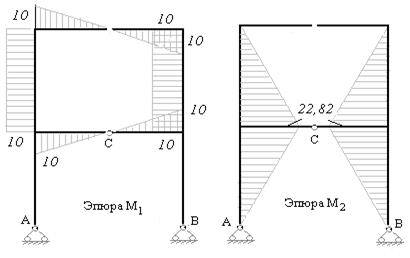
Рис.7.14 Рис.7.15
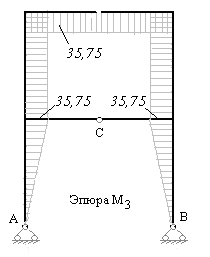
Рис.7.16
8) Строим исправленные эпюры изгибающих моментов в основной системе. Для этого умножаем ординаты единичных эпюр на найденные (из решения канонических уравнений) значения неизвестных усилий. На рис.7.14 – 7.15 построены исправленные эпюры изгибающих моментов (используем второй приём построения эпюры изгибающих моментов).
9) Строим эпюру изгибающих моментов в заданной статически неопределимой раме. Для этого в характерных сечениях рамы алгебраически суммируем ординаты трех эпюр изгибающих моментов, построенных в основной системе: грузовой эпюры 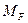 и трех исправленных эпюр
и трех исправленных эпюр 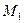 ,
, 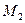 и
и 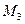 . На рис.7.17 построена эта эпюра.
. На рис.7.17 построена эта эпюра.
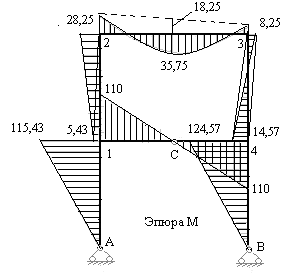
Рис.7.17
10) Проверяем правильность построенной эпюры изгибающих моментов в заданной раме:
а) статическая проверка по условиям равновесия жестких узлов рамы от действия узловых моментов. По эпюре видно, что все четыре жесткие узлы рамы 1.2.3 и 4 находятся в равновесии, т.е. сумма узловых изгибающих моментов в каждом жестком узле равна нулю;
б) деформационная проверка состоит в том, что перемещение в раме по направлению любой неизвестной метода сил должно быть равным нулю
Найдем, например, перемещение по направлению 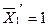 (рис.7.18), во втором варианте основной системы. Для этого построим единичную эпюру изгибающих моментов
(рис.7.18), во втором варианте основной системы. Для этого построим единичную эпюру изгибающих моментов 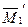 и перемножим по правилу Верещагина эпюру
и перемножим по правилу Верещагина эпюру 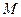 на единичную эпюру
на единичную эпюру 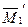 . Предварительно сложные эпюры расчленяем на простые так, чтобы их площади и положения центров тяжести легко определялись. На рис.7.17 и 7.18 показано разделение сложных эпюр на простые эпюры. Криволинейная эпюра на верхнем ригеле разделена на параболический сегмент, имеющий ординату 54 по середине ригеля и трапецию. На стойках трапеции разделены на два треугольника. Тогда:
. Предварительно сложные эпюры расчленяем на простые так, чтобы их площади и положения центров тяжести легко определялись. На рис.7.17 и 7.18 показано разделение сложных эпюр на простые эпюры. Криволинейная эпюра на верхнем ригеле разделена на параболический сегмент, имеющий ординату 54 по середине ригеля и трапецию. На стойках трапеции разделены на два треугольника. Тогда:
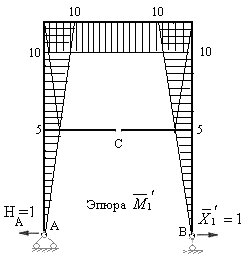
Рис.7.18
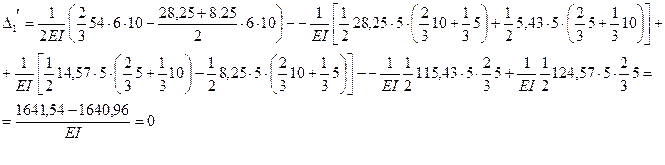 Таким образом, деформационная проверка выполняется. Следовательно, эпюра изгибающих моментов в заданной раме построена правильно.
Таким образом, деформационная проверка выполняется. Следовательно, эпюра изгибающих моментов в заданной раме построена правильно.
11) Используя правило Журавского, определяем поперечные силы на участках рамы, где эпюра М прямолинейна. Рама имеет пять таких участков:
Участок А-1. 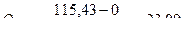 кН.
кН.
Участок 1-2. 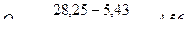 кН.
кН.
Участок 1-4. 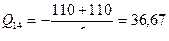 кН.
кН.
Участок 3-4. 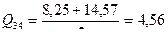 кН.
кН.
Участок 4-В. 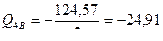 кН.
кН.
Определяем поперечные силы на концах участка 2-3, загруженного равномерно распределенной нагрузкой. Для этого используем формулы (7.17) и (7.18):
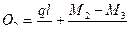 ,
,
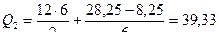 кН.
кН.
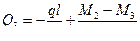
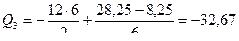 кН.
кН.
На рис.7.19 построена эпюра поперечных сил. Поперечные силы со знаком плюс отложены вверх от осей каждого ригеля рамы, и влево от осей каждой стойки. Поперечные силы со знаком минус откладываются противоположно.
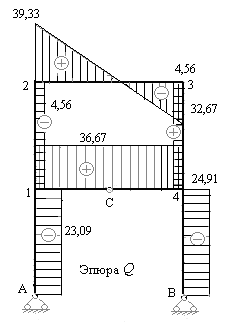
Рис.7.19
12) Определяем продольные силы в стержнях рамы, пользуясь методом равновесия узлов. Вырезаем сначала узлы 2 и 3, а затем узлы 1 и 4. Эти узлы загружаем неизвестными продольными усилиями, направленными от узлов, и известными поперечными силами в рассеченных стержнях. Величины и направления поперечных сил устанавливаются по эпюре поперечных сил (рис.13). Поперечная сила, имеющая знак плюс должна вращать узел по часовой стрелке, а поперечная сила, имеющая знак минус должна вращать узел против часовой стрелки. На рис.14 показаны все силы, действующие на каждый узел рамы.
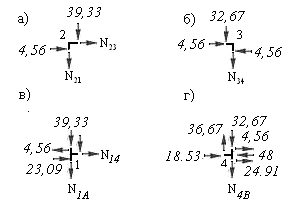
Рис.7.20
Для каждого узла рамы составляем два уравнения равновесия, используя следующие два условия:
 и
и 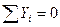 .
.
Узел 2 (рис.7.20,а):
 ,
, 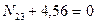 ,
, 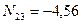 кН.
кН.
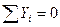 ,
, 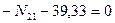 ,
, 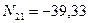 кН.
кН.
Узел 3 (рис.7.20,б):
 ,
, 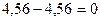 ,
, 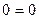 (проверка).
(проверка).
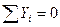 ,
, 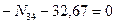 ,
, 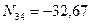 кН.
кН.
Узел 1 (рис.7.20,в):
 ,
, 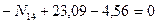 ,
, 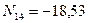 кН.
кН.
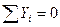 ,
, 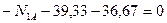 ,
, 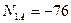 кН.
кН.
Узел 4 (рис.7.20,г):
 ,
, 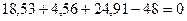 ,
, 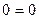 (проверка).
(проверка).
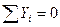 ,
, 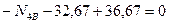 ,
, 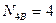 кН.
кН.
Эпюра продольных сил построена на рис.7.21.
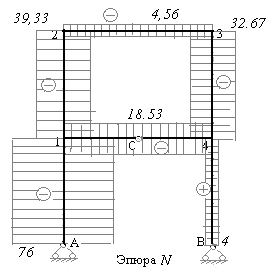
Рис.7.21
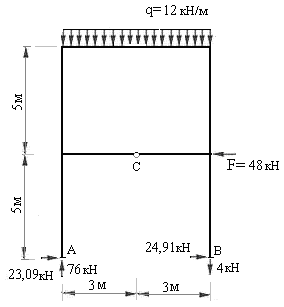
Рис.7.22
13) Проверяем равновесие рамы в целом. Освобождаем раму от опор и загружаем её заданными нагрузками и реакциями освобожденных опорных
связей (рис.7.22)
Величины и направления этих реакций устанавливаем по эпюрам поперечных и продольных сил (рис.7.19 и 7.21).
Составляем три уравнения равновесия рамы, используя условия:
 ,
, 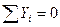 ,
, 
1) 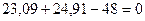 ;
; 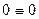
2) 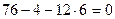 ;
; 
3) 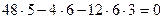 ,
, 
Таким образом, все уравнения равновесия удовлетворяются. Расчет рамы методом сил выполнен без ошибок.
Пример 7.2: Построить эпюры внутренних усилий для статически неопределимой рамы с наклонным ригелем и вертикальными стойками, защемленными у основания (рис.7.23). Жесткости стоек принять равными 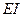 , жесткость ригеля равной
, жесткость ригеля равной 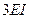 .
.
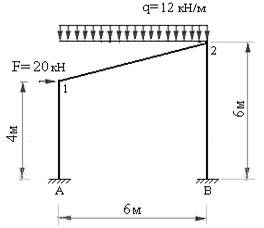
Рис.7.23
Последовательность расчета:
1. Устанавливаем степень статической неопределимости заданной рамы, используя формулу (1.1).
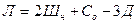 ;
; 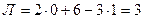 .
.
Таким образом, заданная рама имеет три независимых неизвестных метода сил.
2. Образуем основную систему метода сил. Из всех возможных основных систем, которые предлагаем образовать самостоятельно, выберем расчетную основную систему путем вертикального разреза ригеля в узле 1 заданной рамы (рис.7.24,а). Эта система является статически определимой и состоит из двух неподвижных и геометрически неизменяемых частей: левой стойки А-1 и ломаного стержня 1-2-В.
3. Создаем эквивалентную систему метода сил. Для этого основную систему загружаем заданными нагрузками и неизвестными усилиями 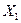
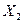 и
и 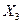 (рис. 7.24,б)
(рис. 7.24,б)
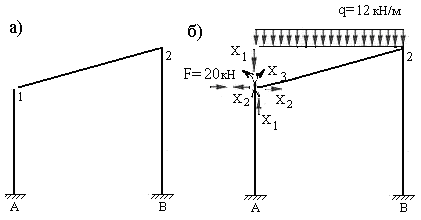
Рис.7.24
4. Записываем систему канонических уравнений метода сил:
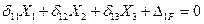
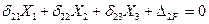 (7.21)
(7.21)
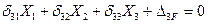
5. Строим единичные эпюры и грузовую эпюру изгибающих моментов в основной системе.
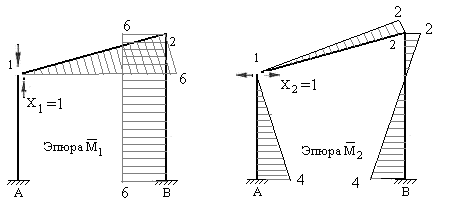
Рис.7.25 Рис.7.26
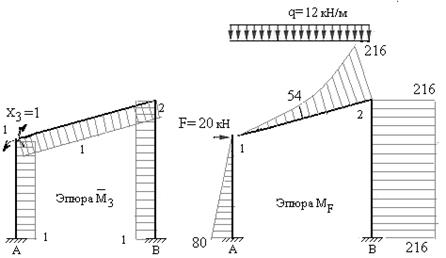
Рис.7.27 Рис.7.28
В отличие от рамы, рассмотренной в примере 1, эти эпюры можно построить, не определяя реакции, которые возникают в защемляющих опорах от заданных нагрузок. Изгибающие моменты определяются по участкам, рассматриваемым от проведенного сечения (разреза) рамы к опорам. На рисунках 7.25-7.28 построены единичные эпюры и грузовая эпюра изгибающих моментов в основной системе. При этом ординаты эпюр отложены перпендикулярно осям стержней со стороны растянутых волокон.
6. Определяем коэффициенты и грузовые перемещения канонических уравнений, пользуясь правилом Верещагина.
Примечание: При перемножении эпюр изгибающих моментов по правилу Верещагина учитывается истинная длина каждого стержня или каждого участка.
Вычислим предварительно длину наклонного ригеля.
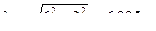 . Тогда найдем:
. Тогда найдем:
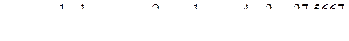
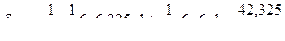
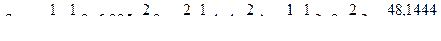
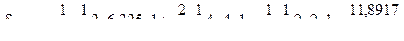
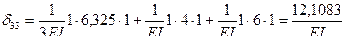
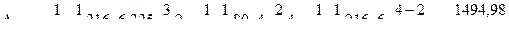
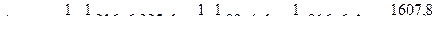
7. Подставляем эти значения в канонические уравнения, переносим грузовые перемещения в правые части и решаем полученную систему уравнений методом уравнивания коэффициентов при неизвестных:
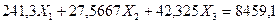
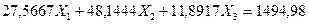 (7.22)
(7.22)
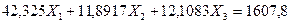
Разделим каждое уравнение на коэффициенты при неизвестном усилии 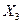 :
:
аждое уравнение на коэффициенты при 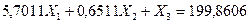 ий авнивания коэффициентов при неовые перемещения в правые части и
ий авнивания коэффициентов при неовые перемещения в правые части и
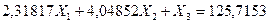 (7.23)
(7.23)
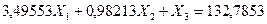
Вычитаем из первого уравнения системы (7.23) второе, а затем третье, получаем новую систему двух уравнений с двумя неизвестными:
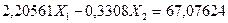 (7.24)
(7.24)
Уравниваем коэффициенты при неизвестном усилии 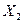 и вычитаем первого полученного уравнения второе:
и вычитаем первого полученного уравнения второе:
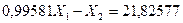
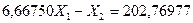 (7.25)
(7.25)
Вычитаем из второго уравнения системы (7.25), первое, находим неизвестное усилие 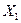 :
: 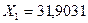 кН. Из первого уравнения системы (7.25) определяем величину неизвестного усилия
кН. Из первого уравнения системы (7.25) определяем величину неизвестного усилия 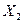 :
: 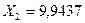 кН. Для проверки правильности вычислений следует подставить во второе уравнения системы (7.25) и убедиться, что оно обращается в тождество
кН. Для проверки правильности вычислений следует подставить во второе уравнения системы (7.25) и убедиться, что оно обращается в тождество 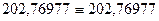 .
.
Из первого уравнения системы (7.23) определяем величину усилия 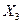 :
:
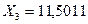 кНм. При подстановке всех найденных значений неизвестных усилий во второе и третье уравнения системы (7.23) они должны тождественно удовлетворяться, аналогично предыдущему.
кНм. При подстановке всех найденных значений неизвестных усилий во второе и третье уравнения системы (7.23) они должны тождественно удовлетворяться, аналогично предыдущему.
8. Строим исправленные эпюры изгибающих моментов в основной системе путем умножения ординат единичных эпюр на значения усилий, полученные из решения канонических уравнений метода сил (рис.7,29 – 7.31).
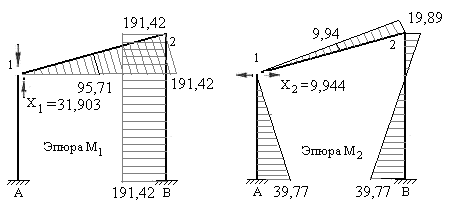
Рис.7.29 Рис.7.30
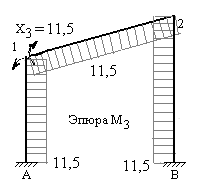
Рис.7.31
Так как все три усилия имеют знак плюс, то их направления, принятые предварительно, верны и исправленные эпюры будут полностью совпадать по виду с единичными эпюрами. Ординаты исправленных эпюр получаем умножением ординат единичных эпюр на значения соответствующих усилий.
9. Строим эпюру изгибающих моментов в заданной статически неопределимой раме. Для этого суммируем ординаты грузовой эпюры и трех исправленных эпюр, построенных в основной системе метода сил, т.е. эпюр, построенных на рис. 7.28 – 7.31. На рис.7.32 построена эпюра изгибающих моментов в заданной раме. Легко подсчитать величины ординат этой эпюры и убедиться в правильности её построения.
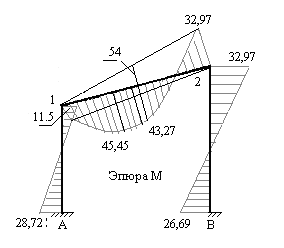
Рис.7.32
10. Осуществим статическую и деформационную проверки эпюры изгибающих моментов.
Рис.7.33
а) Статическая проверка состоит в том, что жесткие узлы рамы 1 и 2 должны находиться в равновесии под действием узловых изгибающих моментов.
Вырезаем жесткие узлы рамы 1 и 2. На эти узлы действуют изгибающие моменты, величины и направления которых, определяем по эпюре изгибающих моментов (моменты действуют из растянутой зоны в сторону сжатой зоны стержней). На рис.7.33 показано загружение узлов узловыми изгибающими моментами. Легко убедиться, что алгебраическая сумма моментов, действующих на каждый узел равна нулю.
б) Деформационная проверка. Выбираем новый вариант основной системы путем замены защемляющих опор рамы шарнирно неподвижными и введения шарнира в узел 2 заданной рамы. В результате получаем трехшарнирную раму (рис.7.34).
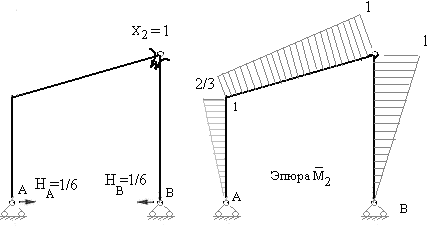
Рис. 7.34 Рис.7.35
Загрузим её единичными моментами 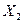 =1, вычислим горизонтальные реакции опор и построим единичную эпюру
=1, вычислим горизонтальные реакции опор и построим единичную эпюру 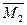 в этой системе (рис.7.35).
в этой системе (рис.7.35).
При перемножении эпюр (рис.7,32) и (рис.7.35) рассматриваем три стержня. На стойках А-1 и В-2 эпюры прямолинейные и их перемножение не вызывает трудностей. На ригеле 1-2 эпюра (рис.7.32) криволинейная, но она может быть разделена на три простые фигуры, площади и положения центров тяжести которых, легко определяются. Этими фигурами являются:
1) квадратичная парабола, имеющая основанием ригель длиною 6,325 м. и максимальную ординату посредине его длины. Эта ордината равна 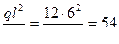 кНм. Площадь такой эпюры равна 2/3 произведения длины на максимальную ординату, а центр тяжести располагается посредине длины ригеля (ордината эпюры
кНм. Площадь такой эпюры равна 2/3 произведения длины на максимальную ординату, а центр тяжести располагается посредине длины ригеля (ордината эпюры 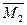 под центром тяжести эпюры М равна половине суммы её ординат на концах ригеля);
под центром тяжести эпюры М равна половине суммы её ординат на концах ригеля);
2) треугольника, расположенного сверху ригеля;
3) треугольника, расположенного снизу ригеля. Площади этих треугольников и положения их центров тяжести легко определяются, а следовательно, легко вычисляются необходимые ординаты единичной эпюры. Вычислим перемещение 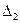 .
.
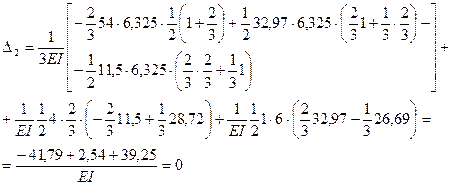
Таким образом, деформационная проверка выполняется. Эпюра изгибающих моментов в заданной раме построена правильно.
11. Определяем поперечные силы в каждом стержне рамы и строим эпюру этих сил.
На стойках рамы эпюра изгибающих моментов ограничена прямыми линиями, наклоненными к оси стержня. Тангенсы углов наклона этих прямых равны поперечным силам, т.е.
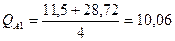 кН,
кН, 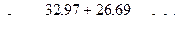 кН
кН
На ригеле 1-2 эпюра изгибающих моментов имеет криволинейное очертание по квадратичной зависимости, поэтому эпюра поперечных сил будет ограничена прямой, наклоненной к оси ригеля.
Для построения такой эпюры достаточно вычислить две её ординаты в сечениях 1 и 2 ригеля. Воспользуемся методом равновесия дисков. Вырезаем ригель 1-2 из рамы и загружаем его: заданной равномерно распределенной нагрузкой интенсивностью 12 кн/м, известными изгибающими моментами в сечениях 1 и 2 (их величины и направления устанавливаем по эпюре изгибающих моментов), а также неизвестными поперечными силами в сечениях 1 и 2 ригеля. Эти силы направляем перпендикулярно оси ригеля так, чтобы они вращали вырезанный стержень по часовой стрелке (рис.7.36).
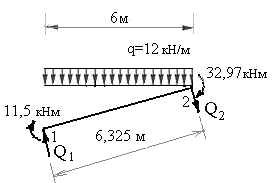
Рис.7.36
Составляем два уравнения равновесия стержня 1-2, используя рациональные условия равновесия:


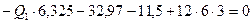

 кН.
кН.
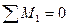

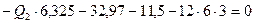

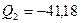 кН.
кН.
На рис.7.37 построена эпюра поперечных сил.
12. Определяем продольные силы в стержнях заданной рамы, пользуясь методом равновесия узлов.
Вырезаем узлы 1 и 2 рамы и загружаем их заданными нагрузками (к узлу 1 приложена сила 20 кн, направленная вправо), известными поперечными силами (величины и направления этих сил устанавливаем по эпюре поперечных сил), а также неизвестными продольными силами, которые
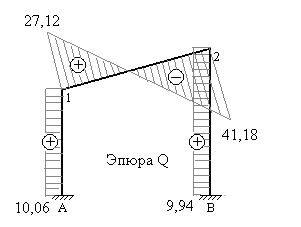
Рис.7.37
направляем от узлов (в соответствии с предполагаемым растяжением стержней). На рис.7.38 показано загружение узлов 1 и 2 заданной рамы.
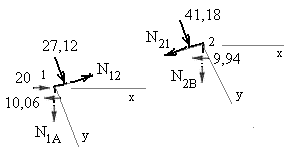
Рис.7,38
Выбираем для каждого узла систему координат так, чтобы одна из осей была перпендикулярной к одному неизвестному усилию, а другая ось перпендикулярна к другому неизвестному усилию. В этом случае уравнения равновесия будут разделенными относительно неизвестных.
Составляем уравнения равновесия узла 1:
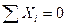

 ,
,
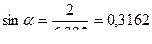
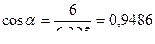 , тогда
, тогда
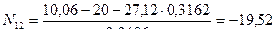 кН
кН
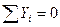

 , тогда:
, тогда:
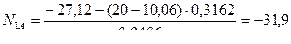 кН.
кН.
Составляем уравнения равновесия узла 2:
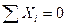

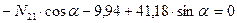 ,
,
откуда
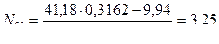 кН.
кН.
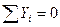

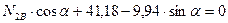 ,
,
откуда
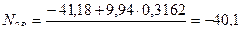 кН.
кН.
На рис.7.39 построена эпюра продольных сил для заданной рамы.
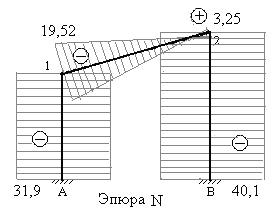
Рис.7.39
13. Проверяем равновесие рамы в целом.
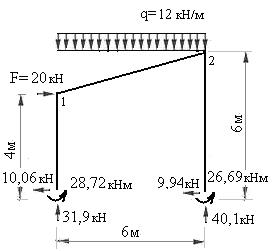
Рис.7.40
Для этого освобождаем её от опор и загружаем заданными нагрузками и реакциями опорных связей. Величины и направления реакций опор устанавливаем по эпюрам изгибающих моментов, поперечных и продольных сил. На рис.7.40 показано загружение рамы, при котором она должна удовлетворять трем условиям равновесия статики.
Составим уравнения равновесия и убедимся, что они тождественно удовлетворяются:
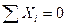

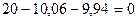

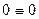
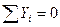

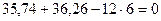

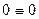



Таким образом, расчет заданной статически неопределимой рамы выполнен правильно.
Пример 7.3. Построить эпюры изгибающих моментов, поперечных и продольных сил для двухпролетной одноэтажной рамы при заданных нагрузках (рис.7.41).
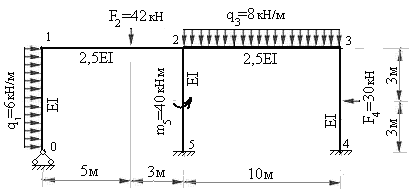 Рис.7.41
Рис.7.41
Последовательность расчета:
1. Устанавливаем степень статической неопределимости заданной рамы, используя формулу (1.1).
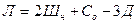 ;
; 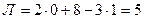 .
.
Таким образом, заданная рама имеет пять независимых неизвестных метода сил, т.е. она является пять раз статически неопределимой.
2. Образуем основную систему метода сил путем освобождения 5-ти лишних связей. На рис.7.42 показан расчетный вариант основной системы. 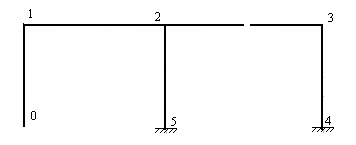
Рис.7.42
Чем выше степень статической неопределимости рамы, тем больше вариантов основной системы метода сил может быть образовано. Предлагаем образовать самостоятельно четыре варианта основной системы, а расчетный вариант основной системы образуем путем вертикального разреза ригеля 2-3 рамы посередине второго пролета и удаления шарнирно-неподвижной опоры 0 (рис.7.42). Эта система является статически определимой и состоит из двух неподвижных и геометрически неизменяемых частей: левого ломаного стержня, защемленного у основания 5 средней стойки и ломаного правого стержня, защемленного у основания 4 правой стойки.
3. Создаем эквивалентную систему метода сил. Для этого основную систему загружаем заданными нагрузками и неизвестными усилиями 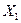 ,
, 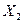 ,
, 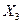 ,
, 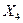 и
и 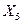 (рис 7.43).
(рис 7.43).
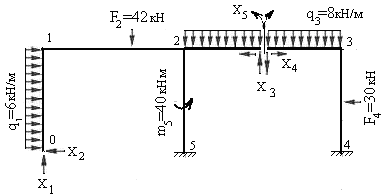
Рис.7.43
4. Записываем систему канонических уравнений метода сил:
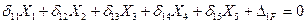
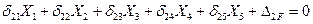
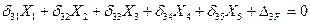 (7.25)
(7.25)
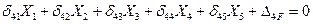
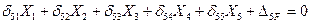
5. Строим единичные эпюры изгибающих моментов и грузовую эпюру в основной системе. Как в примере 2, эти эпюры можно построить, не определяя реакции, которые возникают в защемляющих опорах от заданных нагрузок. Изгибающие моменты определяются по участкам, рассматриваемым от свободных (не закрепленных) концов стержней к опорам.
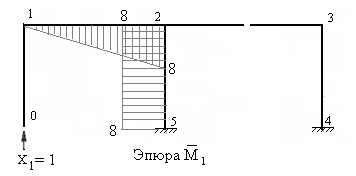
Рис.7.44
На рисунках 7.44 – 7.49 построены единичные эпюры и грузовая эпюра изгибающих моментов в основной системе. Напоминаем, что ординаты эпюр изгибающих моментов должны быть отложены перпендикулярно осям стержней со стороны растянутых волокон.
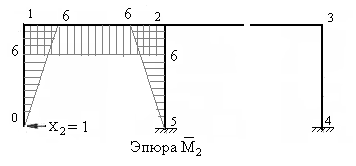
Рис.7.45
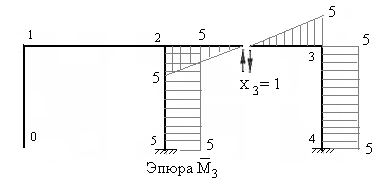
Рис.7.46
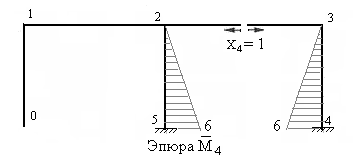
Рис.7.47
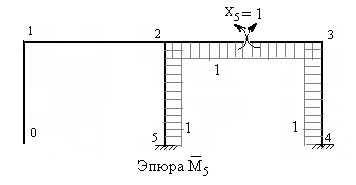
Рис.7.48
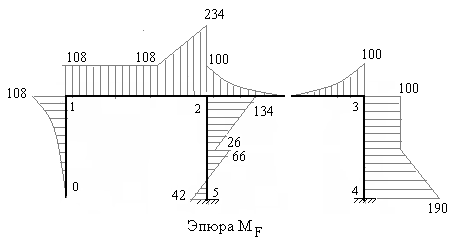
Рис.7.49
6. Определяем коэффициенты и грузовые перемещения канонических уравнений, пользуясь правилом Верещагина:
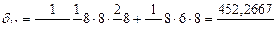 ,
,
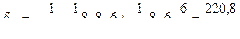 ,
,
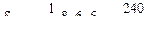 ,
, 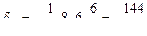 ,
,
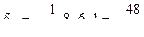 ;
;
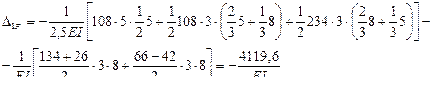
 ,
,  ,
,
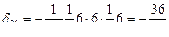 ,
, 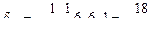 ;
;
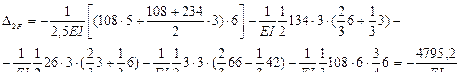
 ,
,
 ,
,
 ;
;

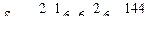 ,
,
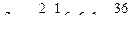 ;
;
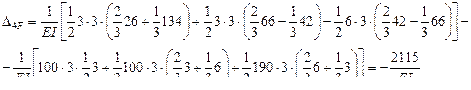
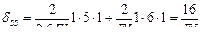
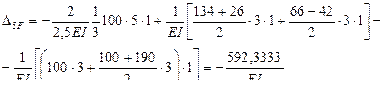
7. Подставляем эти значения в канонические уравнения, умножаем на жесткость 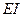 , переносим грузовые перемещения в правые части и решаем полученную систему уравнений методом уравнивания коэффициентов при неизвестных:
, переносим грузовые перемещения в правые части и решаем полученную систему уравнений методом уравнивания коэффициентов при неизвестных:
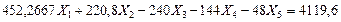
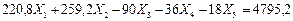
 (7.26)
(7.26)
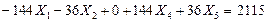

Уравниваем коэффициенты при неизвестном усилии 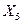 . Для этого первое уравнение делим на -48, второе уравнение делим на -18, четвертое и пятое уравнения делим соответственно на 36 и 16. Третье уравнение разделим на 333,3333. В результате получим систему уравнений (7.27):
. Для этого первое уравнение делим на -48, второе уравнение делим на -18, четвертое и пятое уравнения делим соответственно на 36 и 16. Третье уравнение разделим на 333,3333. В результате получим систему уравнений (7.27):

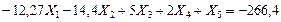
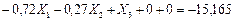 (7.27)
(7.27)


Вычитаем последовательно из первого уравнения системы (7.27) второе, четвертое и пятое уравнения и сохраняем третье уравнение без пятого слагаемого левой части, в результате получим:
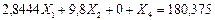
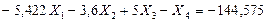
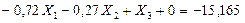 (7.28)
(7.28)
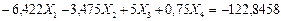
Исключаем в этой системе неизвестное усилие 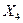 и получаем систему трех уравнений с тремя неизвестными:
и получаем систему трех уравнений с тремя неизвестными:
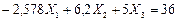
 (7.29)
(7.29)
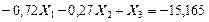
Уравниваем коэффициенты при неизвестном усилии 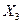 :
:
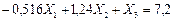
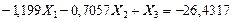 (7.30)
(7.30)
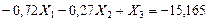
Вычитаем последовательно из первого уравнения второе и третье, получаем:
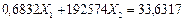
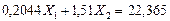 (7.31)
(7.31)
Уравниваем коэффициенты при неизвестном усилии 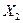 :
:
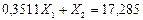
 (7.32)
(7.32)
Вычитаем из первого уравнения второе, получаем:
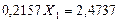 , откуда
, откуда 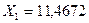 кН. Из первого уравнения системы (7.31) определяем величину усилия
кН. Из первого уравнения системы (7.31) определяем величину усилия 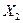 :
: 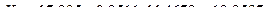 кН. Второе уравнение системы (7.31) используем для проверки выполненных вычислений:
кН. Второе уравнение системы (7.31) используем для проверки выполненных вычислений: 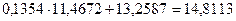 , откуда
, откуда 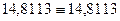 .
.
Из первого уравнения системы (7.30) определяем величину неизвестного усилия 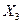 :
:  кН.
кН.
После подстановки величин трех найденных усилий во второе и третье уравнения системы (7.30) получаем тождественное равенство их левых и правых частей:
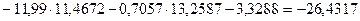 , откуда
, откуда 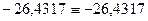 .
.
 , откуда
, откуда 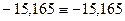 .
.
Величину неизвестного усилия 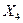 определяем из первого уравнения системы (7.28):
определяем из первого уравнения системы (7.28):
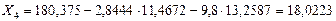 кН.
кН.
Остальные три уравнения системы (2.11) обращаются в тождества при подстановке значений найденных усилий.
Величину неизвестного усилия 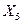 определяем из первого уравнения системы (7.27):
определяем из первого уравнения системы (7.27):
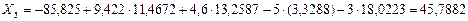 кНм.
кНм.
Остальные четыре уравнения системы (7.27) обращаются в тождества при подстановке значений найденных усилий.
8. Строим исправленные эпюры изгибающих моментов в основной системе. Для этого ординаты единичных эпюр умножаем на соответствующие значения найденных усилий с учетом их знаков. Если усилие имеет знак плюс, то исправленная эпюра совпадает по виду с единичной эпюрой, но имеет другие ординаты. Если же усилие имеет знак минус, то исправленная эпюра имеет зеркальное изображение
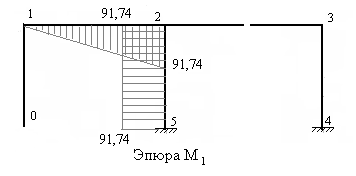
Рис.7.50
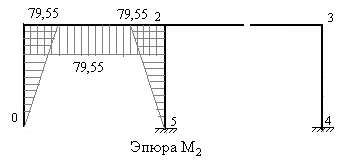
Рис.7.51
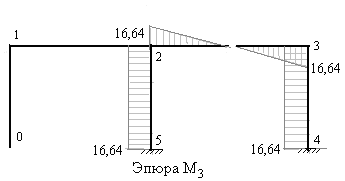
Рис.7.52
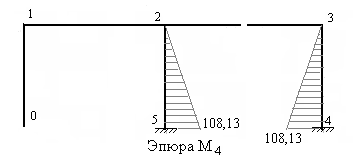
Рис.7.53
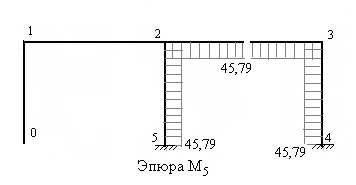
Рис.7.54
единичной эпюры, т.е. единичную эпюру необходимо повернуть вокруг оси каждого стержня на угол равный 1800 и её ординаты умножить на модуль усилия. В рассматриваемом примере ординаты исправленной эпюры М3 откладываем от оси каждого стержня, противоположно ординатам единичной эпюры. На рис.7.50 – 7.54 построены исправленные эпюры.
9. Строим эпюру изгибающих моментов в заданной статически неопределимой раме. Ордината эпюры изгибающих моментов в любом сечении заданной рамы равна алгебраической сумме ординат, взятых в том же сечении грузовой эпюры и всех исправленных эпюр. На рис 7.55 построена эпюра изгибающих моментов в заданной раме. Рекомендуем проверить правильность вычисления ординат этой эпюры в характерных сечениях каждого стержня заданной рамы, а также осуществить статическую и деформационную проверки, как было выполнено в примерах 1 и 2.
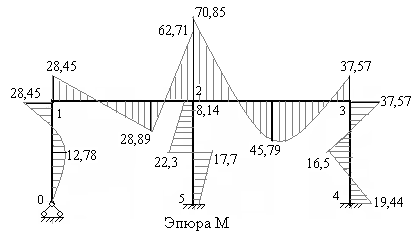
Рис.7.55
10. Вычисляем поперечные силы на отдельных участках рамы по формуле Журавского (на участках, где эпюра М прямолинейна) или по методу равновесия дисков (на участках, где эпюра М криволинейна). На рис.7.56 построена эпюра поперечных сил. Предлагаем проверить правильность вычисления ординат этой эпюры.
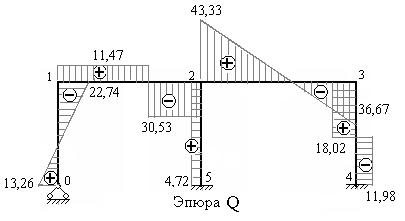
Рис.7.56
11. Вычисляем продольные силы в стержнях заданной рамы, пользуясь методом равновесия узлов, и строим эпюру N (рис.7.57).
Предлагаем проверить ординаты эпюры продольных сил и выполнить проверку равновесия рамы в целом, как было выполнено в примерах 1 и 2.
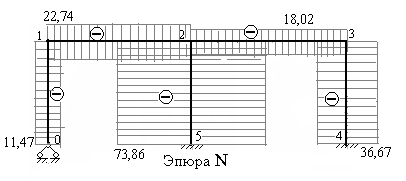
Рис.7.57
Вопросы для самоконтроля полученных знаний.
1. Какая система является статически неопределимой?
2. Как степень статической неопределимости связана с числом степеней свободы?
3. Какова степень статической неопределимости замкнутого бесшарнирного. контура?
4. Как определить степень статической неопределимости системы, исходя из понятия о замкнутом контуре?
5. Какие системы относят к внутренне статически неопределимым?
6. Назовите три основных метода расчета статически неопределимых систем.
7. Что принимается в качестве неизвестных метода сил?
8. Что представляет собой основная система метода сил?
9. В чем различие между абсолютно необходимыми и условно необходимыми связями?
10. Могут ли абсолютно необходимые связи считаться лишними?
11. Приведите возможные способы отбрасывания связей.
12. Что представляют собой канонические уравнения метода сил?
13. Что представляют собой коэффициенты и свободные члены канонических уравнений метода сил?
14. Какой метод положен в основу определения коэффициентов и свободных членов канонических уравнений?
15. Каково свойство главных коэффициентов канонических уравнений?
16. Как можно определить усилия в заданной системе после определения лишних неизвестных?
17. Как проверить правильность вычисления коэффициентов и свободных членов канонических уравнений?
18. Как проверить правильность расчета статически неопределимой системы методом сил?
19. Какие способы применяются для упрощения расчета симметричных систем методом сил?
20. Какие преимущества дает выбор симметричной системы метода сил при расчете на: а) произвольную нагрузку, б) симметричную и в) кососимметричную нагрузку?
21. Как определить перемещение в статически неопределимой системе?
Дата: 2019-02-02, просмотров: 1260.