Элементы трехшарнирных арок, очертание их оси и характеристики оси в сечениях арки.
Трехшарнирной аркой называют стержневую систему, состоящую из двух криволинейных дисков, объединенных между собой ключевым шарниром, и закрепленных на концах шарнирно неподвижными опорами.
На рис.4.1 показана трехшарнирная арка. Её элементами являются:
- криволинейные диски АС и ВС, которые называют полуарками;
- ключевой шарнир С и опорные (пятовые) шарниры А и В;
- опорная прямая АВ, которая проходит через центры опорных шарниров;
- пролет арки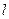 
и горизонтальные проекции полуарок 
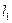и 
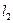, называемые полупролетами арки;
стрела подъема арки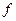 
, равная расстоянию от ключевого шарнира до опорной прямой.
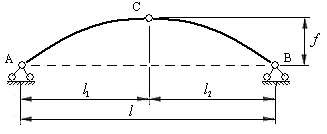
Рис.4.1
Опорные шарниры арки, как правило, располагаются в одном уровне, т.е. опорная прямая является горизонтальной прямой. С этой прямой совмещается горизонтальная ось системы координат. Начало системы координат принимается в центре левого опорного шарнира.
Очертание оси арки может быть задано уравнением квадратичной параболы или уравнением окружности. В первом случае арку называют параболической, а во втором – циркульной.
Рассмотрим трехшарнирную арку, отнесенную к системе осей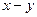 
(рис.4.2).
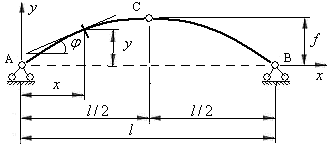
Рис.4.2
Любое сечение оси арки, взятое на расстоянии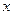 
от начала координат будет иметь ординату 
, определяемую из уравнения, принятого для очертания оси арки.
При параболическом очертании арки ордината 
вычисляется из уравнения:
(4.1)
При циркульном очертании арки ордината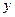 
вычисляется из уравнения:
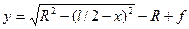, (4.2)
где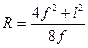 
(4.3)
Проведем касательную к оси арки в заданном сечении и обозначим через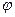 
угол её наклона к горизонтальной оси 
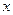. Тогда при параболическом очертании оси арки тангенс этого угла будет определяться по формуле:
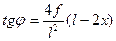(4.4)
Синус и косинус того же угла находят по известным формулам тригонометрии:
, 
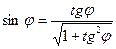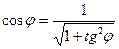(4.5)
При очертании оси арки по окружности тригонометрические функции угла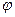 
вычисляются по формулам:
, 
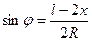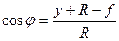(4.6)
Опоры трехшарнирных арок могут располагаться в разных уровнях (рис.4.3).
Для таких арок ось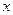 
совмещается с опорной прямой АВ , а ось 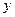направляется перпендикулярно к оси 
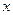. Характеристики сечений оси арки определяются по приведенным выше формулам, при замене в них длины пролета арки длиной опорной прямой, т.е величиной 
.
Расчет таких арок сложнее, чем арок с опорами в одном уровне и в данном пособии не приводится.
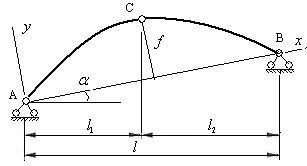
Рис.4.3
Трехшарнирные рамы.
Трехшарнирные рамы отличаются от трехшарнирных арок тем, что их диски являются прямолинейными на отдельных участках. На рис.4.4 представлена наиболее применяемая трехшарнирная рама. Вертикальные стержни рамы называются стойками, а горизонтальные – ригелями. Стойки объединяются жестко с ригелями в узлах 1 и 2, образуя Г – образные диски (полурамы). Эти диски объединяются между собой ключевым шарниром С и закрепляются при помощи шарнирно неподвижных опор А и В.
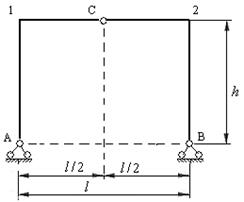
Рис.4.4
Опоры трехшарнирных рам могут располагаться в разных уровнях (рис.4.5).
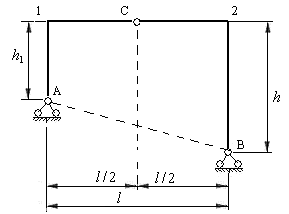
Рис.4.5
При строительстве инженерных сооружений могут быть использованы рамы с наклонными стойками и горизонтальным ригелем, а также рамы с вертикальными стойками и наклонными ригелями (рис.4.6 и 4.7).
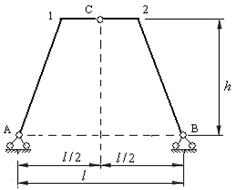
Рис.4.6
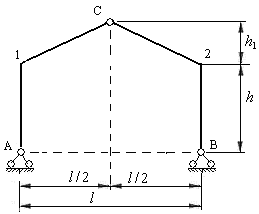
Рис.4.7
4.3 Аналитический метод определения реакций опор трехшарнирной арки.
Рассмотрим трехшарнирную арку, загруженную системой вертикальных сосредоточенных сил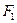 
, 
,… 
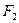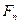(рис.4.8,а) и однопролетную балку на двух шарнирных опорах, имеющую тот же пролет и загруженную теми же нагрузками, что и арка (рис.4.8,б).
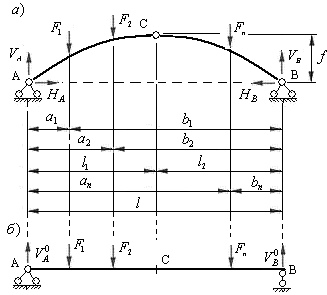
Рис.4,8
Обе опоры трехшарнирной арки шарнирно неподвижные и в них возникают по две составляющие реакций: вертикальные и горизонтальные. Обозначим вертикальные составляющие буквам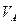и 
и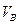 
, а горизонтальные составляющие буквам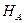и 
и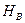 
.
В опорах балки при вертикальных нагрузках возникают только вертикальные реакци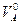и, 
и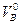 
. Определим сначала вертикальные реакции опор балки из условий её равновесия относительно опорных шарниров:
,
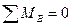
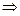
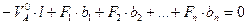Откуда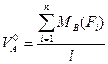 
(4.7)
,
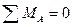
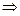
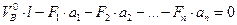Откуда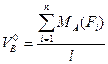 
(4.8)
Определим внутренние усилия в сечении С балки, расположенном под ключевым шарниром арки. Эти усилия будем называть балочными усилиями, т.е балочной поперечной силой в сечении балки под ключевым шарниром арки:
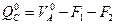(4.9)
и балочным изгибающим моментом в том же сечении:
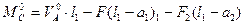(4.10)
Перейдем к определению реакций опор трехшарнирной арки.
Для определения четырех неизвестных реакций опор арки, показанных на рис.4.8,а необходимо составить четыре уравнения. Три из них составляем из условий равновесия арки в целом, а четвертое – из условия равновесия одной полуарки по отношению к другой. Такое равновесие возможно, если изгибающий момент в ключевом шарнире арки равен нулю. Запишем условия равновесия, составим уравнения равновесия и найдем все составляющие реакций опор арки из их решения:
1) 
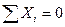
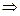
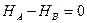
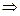
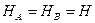(1.11)
Из равенства (1.11) следует, что при загружении арки вертикальными нагрузками горизонтальные составляющие реакций опор равны по модулю и противоположно направлены внутрь пролета арки. Они называются распором арки. Эти силы удерживают опоры арки на заданном расстоянии.
2) 
,
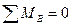
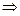
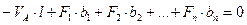Откуда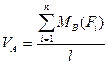 
(4.12)
3) 
,
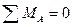
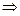
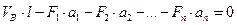Откуда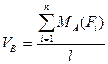 
(4.13)
Сопоставляя выражения (4.7) с (4.12) и (4.8) с (4.13) легко заметить, что вертикальные составляющие реакций опор арки и балки одинаковы, если балка имеет тот же пролет и несет те же нагрузки, что и арка.
4) 
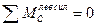
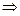
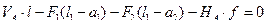(4.14)
Учитывая, что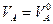 
, а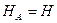 
и используя выражение (4.10), равенство (4.14) приведем к виду:
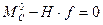, откуда
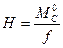(4.15)
Таким образом, распор арки равен отношению балочного изгибающего момента в сечении, взятом под ключевым шарниром арки к стреле подъема арки.
4.4 Аналитический метод определения внутренних усилий в сечениях трехшарнирной арки.
Рассмотрим трехшарнирную арку, загруженную вертикальными силами (рис.4.9,а), а также балку на двух шарнирных опорах, имеющую тот же пролет и загруженную теми же силами, что и арка (рис.4.9,б). Реакции опор и распор арки определяем по формулам (4.12), (4.13) и (4.15).
Проведем нормальные сечения 
арки и балки с абсциссой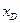 
. В сечении арки проведем касательную к оси и обозначим угол её наклона к горизонтальной прямой, через 
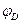. Ордината сечения арки 
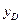определяется из уравнения очертания оси арки, а тангенс угла 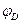из производной от этого уравнения по абсциссе .
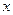Рис.4.9
Отбросим правые отсеченные части арки и балки, а их действие на левые части, заменим внутренними усилиями в сечении. В сечении балки действуют две составляющие: поперечная сила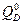 
и изгибающий момент 
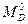(рис.4.10,б), а в сечении арки действуют три составляющие внутренних усилий: поперечная сила 
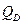, продольная сила 
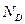и изгибающий момент 
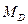(рис.4.10,а). На рис.4.10 показаны направления усилий, соответствующие их положительным знакам.
Определим балочные усилия в сечении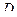 
, используя два условия равновесия левой отсеченной части балки (рис.4.10,б):
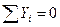
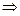
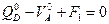откуда 
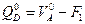(4.16)
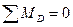
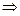
, откуда:
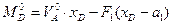(4.17)
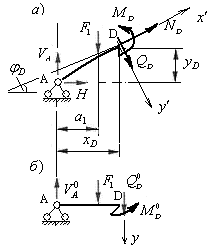
Рис.4.10
Определим арочные усилия в сечении 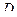, используя три условия равновесия левой отсеченной части арки (рис.4.10,а):
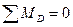
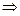
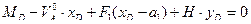
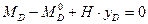, откуда:
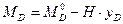(4.18)
Итак, изгибающий момент в произвольном сечении трехшарнирной арки равен разности между балочным изгибающим моментом в соответствующем сечении и произведением распора арки на ординату её оси в заданном сечении.
Изгибающий момент принимается со знаком плюс, если он растягивает нижние волокна арки, т.е. если он стремится повернуть левую отсеченную часть против часовой стрелки, а правую отсеченную часть по часовой стрелке. При противоположных направлениях действия, изгибающий момент принимается со знаком минус.
Из формулы (4.18) следует, что изгибающий момент в любом сечении арки имеет значительно меньшее значение, чем балочный изгибающий момент.
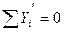
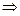
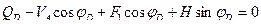
Откуда: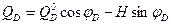 
(4.19)
Итак, поперечная сила в произвольном сечении арки равна разности произведений балочной поперечной силы на косинус угла наклона касательной и распора арки на синус того же угла.
Поперечная сила в сечении принимается со знаком плюс, если она стремится повернуть любую отсеченную часть арки по часовой стрелке и со знаком минус, если она стремится повернуть любую часть арки против часовой стрелки.
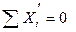
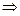
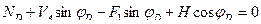
Откуда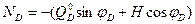 
(4.20)
Дата: 2019-02-02, просмотров: 419.
