Многопролетные статически определимые балки относятся к плоским стержневым системам, образованным по первому варианту и состоящих из прямолинейных дисков, объединенных между собой цилиндрическими шарнирами и закрепленных с помощью опорных устройств.
Диски многопролетных балок могут иметь одинаковую изгибную жесткость, либо разную. Это не влияет на распределение усилий в статически определимых системах.
Один из дисков балки должен быть закреплен тремя опорными связями (при помощи одной защемляющей опоры, либо двух шарнирных опор, одна из которых неподвижна, а друга подвижна в направлении оси диска). Такой диск многопролетной балки называют главным. Главный диск может являться балкой-консолью, либо двухопорной балкой с одной, или двумя консолями. Длины консолей влияют на распределение усилий и устанавливаются расчетом.
К главному диску присоединяется другой диск при помощи шарнира и одной шарнирно подвижной опоры. Напомним, что шарнир имеет две связи и эквивалентен шарнирно неподвижной опоре. Этот диск называют передаточным, если к нему присоединяется следующий диск, или подвесным, если он является крайним диском балки.
На рис.2.1 показана балка, имеющая три диска. Диск АС является главным, диск СЕ – передаточным, диск ЕК – подвесным. Такую балку называют регулярной или балкой Семиколенова.
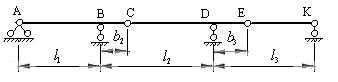
Рис.2.1
Расстояния между соседними опорами называют пролетами балки. Их длины обозначают 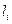 и измеряют в метрах.
и измеряют в метрах.
Расстояния от шарниров до ближних опор принимают в пределах (1/3 – 1/4) длин соответствующих пролетов, т.е.
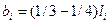
Многопролетные балки могут иметь несколько главных дисков, несколько передаточных дисков и несколько подвесных дисков. Если балка имеет несколько главных дисков, то один из них должен иметь три опорные связи, а остальные по две шарнирно подвижные опоры. Передаточные диски всегда имеют одну шарнирно подвижную опору, а подвесные диски могут объединять два диска при помощи двух шарниров и не иметь наземных опор. На рис.2.2 представлена балка, состоящая из двух главных дисков (AB и CK) и двух подвесных дисков (BC и KL), а на рис.2.3 показана балка, имеющая главный диск AB, два передаточных диска (BD и DK) и подвесной диск KL.
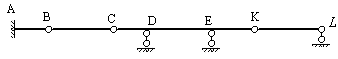
Рис.2.2
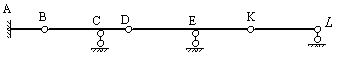
Рис.2.3
Многопролетные статически определимые балки имеют простые конструктивные решения, позволяют использовать простые методы определения реакций опор и внутренних усилий в произвольных сечениях, а также регулировать усилия путем смещения шарниров в пролетах.
Поэтажной схемой многопролетной балки называют схему взаимодействия отдельных дисков балки, каждый их которых представляет отдельную однопролетную балку с одной или двумя консолями. Для образования поэтажной схемы необходимо установить главные диски и вычертить их в масштабе длин на уровне первого этажа. Затем трансформировать цилиндрические шарниры, объединяющие диски в шарнирно неподвижные опоры и вычертить на уровне второго и последующих этажей передаточные и подвесные диски.
Образуем, к примеру, поэтажную схему балки, показанной на рис.2.1. Эта балка состоит из главного диска АС, передаточного диска СЕ и подвесного диска ЕК.
Вычерчиваем диск АС на уровне первого этажа рис.2.4. На этот диск в точке С устанавливаем шарнирно неподвижную опору передаточного диска СЕ и вычерчиваем этот диск на уровне второго этажа. Аналогично в точке Е передаточного диска устанавливаем шарнирно неподвижную опору подвесного диска ЕК и вычерчиваем этот диск на уровне третьего этажа.
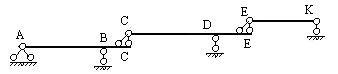
Рис.2.4
На рис.2.5 и 2.6 показаны поэтажные схемы балок, представленных на рис.2.2 и 2.3 соответственно. Рекомендуем установить категории дисков этих балок и обосновать образованные поэтажные схемы.
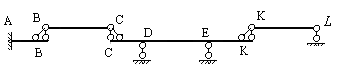
Рис.2.5
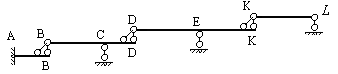
Рис.2.6
2.2 Аналитические методы определения реакций опор многопролетных балок
Для определения реакций, возникающих в опорах загруженной многопролетной балки, используют два метода:
- метод равновесия дисков;
- метод неполного освобождения связей.
При определении опорных реакций методом равновесия дисков освобождают все связи заданной балки (опорные связи и шарниры, объединяющие диски). В результате получаем D изолированных дисков. Каждый диск загружаем заданными нагрузками и неизвестными реакциями удаленных связей. Цилиндрический шарнир передает от одного диска к другому вертикальные и горизонтальные составляющие реакции. Эти составляющие равны по величине и противоположно направлены. В защемляющей опоре возникают три составляющие реакции (опорный момент, вертикальная и горизонтальная силы), в шарнирно неподвижной опоре возникают вертикальная и горизонтальная составляющие реакции, в шарнирно подвижной опоре возникает только вертикальная реакция.
Таким образом, общее число неизвестных реактивных сил, подлежащих определению, будет равно сумме:
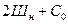 ,
,
где Шн – число цилиндрических шарниров, а
Со - число простых опорных связей балки.
Для определения этих неизвестных составляем 3D уравнений равновесия (по 3 уравнения равновесия для каждого диска). Эти уравнения можно составлять, рассматривая диски в произвольном порядке.
Если число уравнений равновесия равно числу неизвестных сил сопротивления, возникающих в освобожденных связях балки, т.е., если соблюдается равенство:
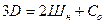 , то рассматриваемая балка статически определима и все неизвестные определяются из решения системы уравнений равновесия. Если число уравнений окажется больше числа неизвестных, то заданная балка геометрически изменяемая или подвижна, а если число уравнений меньше числа неизвестных, балка имеет лишние связи и является статически неопределимой.
, то рассматриваемая балка статически определима и все неизвестные определяются из решения системы уравнений равновесия. Если число уравнений окажется больше числа неизвестных, то заданная балка геометрически изменяемая или подвижна, а если число уравнений меньше числа неизвестных, балка имеет лишние связи и является статически неопределимой.
Примечание. При загружении балки только вертикальными и моментными нагрузками, в шарнирах, а также в неподвижных опорах горизонтальные составляющие реакций равны нулю. В этом случае для каждого диска составляют по два уравнения равновесия, используя рациональные условия.
Таким образом, по методу равновесия дисков определяются одновременно опорные реакции и реакции шарниров.
Рассмотрим пример определения реакций опор и шарниров для балки, представленной на рис.2.7,а.
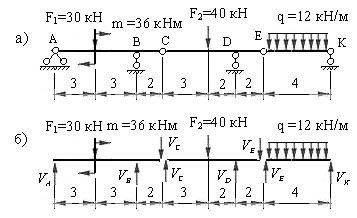
Рис.2.7
Нагрузки и размеры балки в метрах показаны на расчетной схеме балки.
Заданная балка состоит из трех дисков (АС, СЕ и ЕК), объединенных между собой шарнирами С и Е. Опора А шарнирно неподвижная, а опоры В, D и К – шарнирно подвижные в направлении оси балки.
Освободим балку от всех опор и шарниров. В результате получим три изолированных диска (рис.2.7,б). Загружаем каждый диск заданными нагрузками и реакциями удаленных связей. В опорах возникают только вертикальные реакции, которые направляем вверх. Реакции шарниров С и Е действуют на два объединяемых диска. Они равны по величине и направлены вертикально в противоположные стороны. Напомним, что при отсутствии горизонтальных или наклоненных к оси балки нагрузок, горизонтальные реакции шарниров равны нулю. Составляем по два уравнения равновесия для каждого диска, используя условия равенства нулю суммы моментов всех сил приложенных к отдельным дискам относительно двух произвольных точек.
Диск АС.
Условия равновесия: 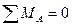 ,
, 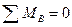
Уравнения равновесия:
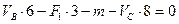 , или
, или 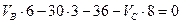 (2.1)
(2.1)
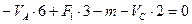 ,или
,или 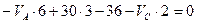 (2.2)
(2.2)
Диск СЕ.
Условия равновесия: 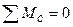 ,
, 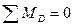
Уравнения равновесия:
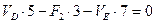 , или
, или 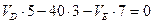 (2.3)
(2.3)
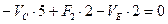 ,или
,или 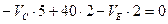 (2.4)
(2.4)
Диск ЕК.
Условия равновесия: 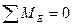 ,
, 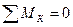
Уравнения равновесия:
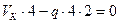 , или
, или 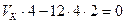 (2.5)
(2.5)
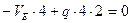 ,или
,или 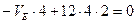 (2.6)
(2.6)
Уравнения (2.1)-(2.4) содержат по 2 неизвестные реакции, уравнения (2.5) и (2.6) по одной неизвестной. Из этих уравнений находим: 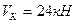 и
и 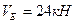
Подставляем значение 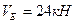 в уравнения (2.3) и (2.4) и находим из их решения
в уравнения (2.3) и (2.4) и находим из их решения 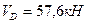 и
и 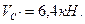
Подставляем значение 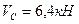 в уравнения (2.1) и (2.2) и находим из их решения
в уравнения (2.1) и (2.2) и находим из их решения 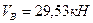 и
и 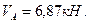
Для проверки правильности решения уравнений равновесия используем условие равенства нулю суммы проекций всех сил, приложенных к балке на вертикальную ось. Эту проверку выполняют для балки в целом. При этом реакции шарниров не учитывают, так как они самоуравновешиваются.

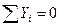
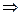
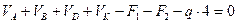 ,
,
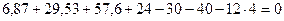
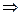
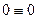
При использовании поэтажной схемы многопролетной балки определение реакций связей упрощается, так как она позволяет установить рациональный порядок рассмотрения дисков и составления уравнений равновесия. Например, для рассмотренной выше балки, поэтажная схема которой представлена на рис.2.4, сначала составляют уравнения равновесия подвесного диска ЕК (смотрите уравнения (2.5) и (2.6)). Из этих уравнений определяют реакции 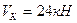 и
и 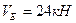 . Затем составляют уравнения равновесия передаточного диска СЕ (уравнения (2.3) и (2.4)), из этих уравнений определяют реакции
. Затем составляют уравнения равновесия передаточного диска СЕ (уравнения (2.3) и (2.4)), из этих уравнений определяют реакции 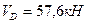 и
и 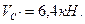 Последним рассматривают равновесие главного диска АС, составляют и решают уравнения (2.1) и (2.2). Получают величины реакций
Последним рассматривают равновесие главного диска АС, составляют и решают уравнения (2.1) и (2.2). Получают величины реакций 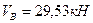 и
и 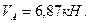
Рассмотрим определение реакций опорных связей методом неполного освобождения связей. При использовании этого метода освобождают только опорные связи заданной балки. В результате получают геометрически изменяемую систему дисков, объединенных между собой шарнирами. Степень её геометрической изменяемости равна числу шарниров балки. Затем загружают балку заданными нагрузками и неизвестными реакциями удаленных опор. Для такой геометрически изменяемой системы необходимо составить три уравнения равновесия в целом (или два уравнения, если нагрузки перпендикулярны к оси балки) и дополнительные уравнения равновесия отдельных частей балки относительно шарниров, объединяющих эти части. Нетрудно заметить, что условия равновесия отдельных частей относительно шарниров, эквивалентны условиям равенства нулю изгибающих моментов в шарнирах балки. Число дополнительных уравнений всегда равно числу шарниров балки. Таким образом, по методу неполного освобождения связей реакции шарниров не определяются, а, следовательно, число неизвестных реакций меньше чем по методу равновесия дисков.
Но уравнения для их определения более сложные, чем в методе равновесия дисков, особенно при большом числе дисков балки. Поэтому метод неполного освобождения связей не рекомендуется применять, если балка имеет более трех дисков.
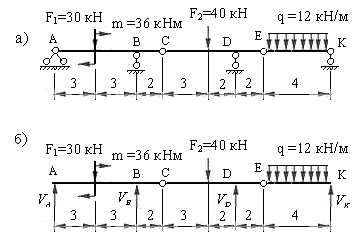
Рис.2.8
Определим реакции опор балки, рассмотренной выше (рис.2.8,а), методом неполного освобождения связей.
Освободим опорные связи заданной балки, а их действие на балку компенсируем приложением вертикальных реакций (рис.2.8,б). Напомним, что при вертикальных нагрузках, горизонтальная реакция неподвижной опоры А не возникает. Для определения четырех неизвестных реакций составляем два уравнения равновесия балки в целом, используя условия: 1) 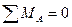 , 2)
, 2) 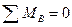 и два дополнительных уравнения, используя условия равенства нулю изгибающих моментов в шарнирах С и Е балки: 3)
и два дополнительных уравнения, используя условия равенства нулю изгибающих моментов в шарнирах С и Е балки: 3) 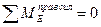 , 4)
, 4) 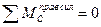 .
.
Составляем четыре уравнения, используя приведенные условия:
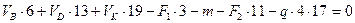 (а)
(а)
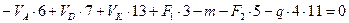 (б)
(б)
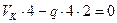 (в)
(в)
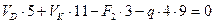 (г)
(г)
Выбираем рациональный порядок решения составленных уравнений:
Из уравнения (в) определяем 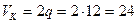 кН.
кН.
Из уравнения (г) определяем
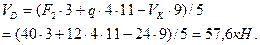
Затем из уравнений (а) и (б) определяем 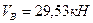 и
и 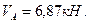
Для проверки вычисленных реакций используем условие: 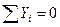
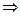
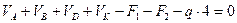 ,
,
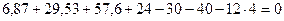
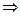
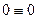
2.3 Методы определения внутренних усилий и построения их эпюр для многопролетных балок
В сечениях многопролетных балок, загруженных поперечными нагрузками, возникают две составляющие внутренних усилий: поперечные силы и изгибающие моменты. Поперечные силы являются равнодействующими касательных сил, распределенных по площади сечения. Они направлены вдоль главной вертикальной оси инерции поперечного сечения. Изгибающие моменты являются равнодействующими моментов нормальных сил относительно оси, направленной перпендикулярно к грузовой плоскости. Напомним правило знаков внутренних усилий в произвольном сечении балки.
Поперечная сила имеет знак + (плюс), если она вызвана силами, направленными вверх слева от сечения, или силами, направленными вниз справа от сечения.
Изгибающий момент имеет знак + (плюс), если он вызван силами направленными вверх независимо от их расположения по отношению к сечению, или моментами, направленными слева от сечения по ходу часовой стрелки, или справа от сечения против хода часовой стрелки.
Усилия принимаются со знаком минус, если нагрузки направлены противоположно.
На рис.2,9 показаны направления нагрузок, при которых в заданном сечении возникают усилия со знаком плюс или минус.
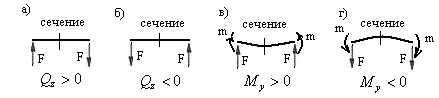
Рис.2.9
Определение внутренних усилий и построение их эпюр для многопролетных балок может быть выполнено методом сечений или методом площадей.
Напомним последовательность построения эпюр указанными методами.
При использовании метода сечений необходимо:
- определить реакции опор заданной балки методом равновесия дисков или методом неполного освобождения связей;
- каждый диск или всю балку разбить на участки, ограниченные точками приложения сосредоточенных сил и моментов, а также границами распределенных нагрузок;
- в пределах каждого участка наметить произвольное сечение на переменном расстоянии xi от начала координат и составить уравнения поперечных сил и изгибающих моментов для каждого участка. В зависимости от характера загружения балки эти уравнения могут быть линейными, квадратичными, или третьей степени относительно переменной xi;
- вычислить необходимое число ординат внутренних усилий и построить их эпюры, т.е. графики изменения поперечных сил и изгибающих моментов по длине балки.
Примечание: если реакции опор балки определяются методом равновесия дисков, используя поэтажную схему заданной балки, то построение эпюр методом сечений целесообразно осуществлять последовательно для каждого диска в одинаковом масштабе, а затем объединить их вдоль оси заданной балки. Если же реакции опор определяются по методу неполного освобождения связей, то построение эпюр осуществляется для всей балки.
При использовании метода площадей построение эпюр поперечных сил и изгибающих моментов осуществляется для всей балки сразу, независимо от метода определения реакций опор. Для этого заданную балку делят на участки и их границы нумеруют слева на право цифрами 0,1,2,3…n. Интервалы загружения балки распределенными нагрузками следует разделить на несколько участков, имеющих равные длины.
Используя известные правила и формулы метода площадей, вычисляют поперечные силы в начале и в конце каждого участка и строят эпюру Qz. Затем вычисляют изгибающие моменты и строят эпюру My.
Напомним правила и формулы метода площадей.
Поперечная сила и изгибающий момент в начале крайнего левого участка всегда известны по условиям закрепления и загружения балки. Они равняются соответственно сосредоточенной силе и сосредоточенному моменту в этом сечении с соответствующими знаками.
2 ) Поперечная сила в конечном сечении произвольного участка 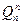 равняется алгебраической сумме поперечной силы в начальном сечении этого участка
равняется алгебраической сумме поперечной силы в начальном сечении этого участка 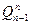 и площади распределенной нагрузки в пределах этого участка.
и площади распределенной нагрузки в пределах этого участка.
Или: 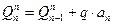 (2.7)
(2.7)
Произведение q·a n равняется площади распределенной нагрузки в пределах участка.
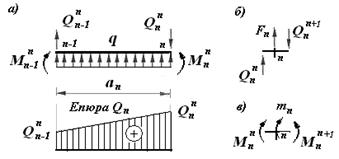
Рис.2.10
Распределенная нагрузка принимается со знаком плюс, если действует вверх и со знаком минус, если действует вниз. На рис.2.10 показаны направления нагрузок и усилий, имеющих знак плюс.
3) Поперечная сила в начальном сечении любого последующего участка 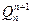 равняется алгебраической сумме поперечной силы в конечном сечении предыдущего участка
равняется алгебраической сумме поперечной силы в конечном сечении предыдущего участка 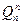 и сосредоточенной силы F n, которая действует на границе этих участков.
и сосредоточенной силы F n, которая действует на границе этих участков.
Или: 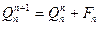 (2.8)
(2.8)
Если на границе двух участков отсутствует сосредоточенная сила, то поперечные силы в конечном сечении предыдущего участка и в начальном сечении последующего участка имеет одинаковое значение, то есть 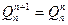 .
.
4) Изгибающий момент в конечном сечении произвольного участка 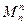 равняется алгебраической сумме изгибающего момента в начальном сечении этого участка
равняется алгебраической сумме изгибающего момента в начальном сечении этого участка 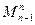 и площади э пюры поперечных сил в пределах этого участка.
и площади э пюры поперечных сил в пределах этого участка.
Или: 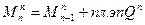 (2.9)
(2.9)
5) Изгибающий момент в начальном сечении любого последующего участка 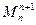 равняется алгебраической сумме изгибающего момента в конечном сечении предыдущего участка,
равняется алгебраической сумме изгибающего момента в конечном сечении предыдущего участка, 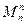 и сосредоточенного момента, который действует на границе этих участков.
и сосредоточенного момента, который действует на границе этих участков.
Или: 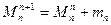 (2.10)
(2.10)
Если на границе двух участков отсутствует внешний сосредоточенный момент, то изгибающие моменты в конечном сечении предыдущего участка и в начальном сечении последующего участка имеет одинаковое значение, то есть 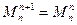 .
.
Пример 2.1. Последовательность построения эпюр поперечных сил и изгибающих моментов методом площадей проследим на примере балки, размеры и нагрузки которой показаны на рис.2.7,а.
Дата: 2019-02-02, просмотров: 527.