Следует иметь в виду, что только неподвижные и геометрически неизменяемые стержневые системы могут воспринимать и удерживать в устойчивом равновесии внешние нагрузки.
Существуют два метода исследования геометрической неизменяемости и неподвижности стержневых систем: кинематический и статический.
Кинематический метод исследования состоит в определении общего числа степеней свободы стержневой системы. Если стержневая система без опорных связей имеет в пространстве 6 степеней свободы, а на плоскости – 3, то она является геометрически неизменяемой. Если стержневая система с опорными связями не имеет степеней свободы, то она является неподвижной.
Используя приведенные определения и формулы (1.2)-(1.5) получаем следующие кинематические условия геометрической неизменяемости и неподвижности систем:
а) Условия геометрической неизменяемости пространственных и плоских систем, образованных по первому варианту:
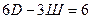 (1.6)
(1.6)
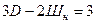 (1.7)
(1.7)
б) Условия геометрической неизменяемости пространственных и плоских систем, образованных по второму варианту:
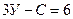 (1.8)
(1.8)
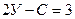 (1.9)
(1.9)
в) Условия неподвижности пространственных и плоских систем, образованных по первому варианту:
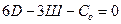 (1.10)
(1.10)
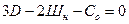 (1.11)
(1.11)
г) Условия неподвижности пространственных и плоских систем, образованных по второму варианту:
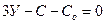 (1.12)
(1.12)
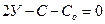 (1.13)
(1.13)
Если при исследовании стержневых систем условия (1.6) – (1.13) выполняются, т.е. левые их части равны правым, то стержневая система является геометрически неизменяемой или неподвижной.
Если же левые части этих условий окажутся большими чем правые, то исследуемая система геометрически изменяема либо подвижна.
Если же левые части этих условий окажутся меньшими чем правые, то исследуемая система имеет лишние связи, т.е. является статически неопределимой.
Следует иметь в виду, что условия (1.6) – (1.13) являются необходимыми, но недостаточными условиями геометрической неизменяемости и неподвижности стержневых систем, так как они не учитывают качественного расположения связей систем. Поэтому кинематический метод необходимо использовать совместно со структурным анализом образования стержневых систем. Структурный анализ базируется на следующих правилах:
1) Два диска на плоскости, объединенные между собой тремя шарнирно стержневыми связями, образуют геометрически неизменяемую систему, если они не параллельные и не пересекаются в одной точке. На рис.1.13,а показано правильное расположение связей в системе двух дисков, а на рис.1.13,б и рис.1.13,в – не правильное их расположение. В первом случае система геометрически неизменяемая, а в двух других случаях она геометрически изменяемая.
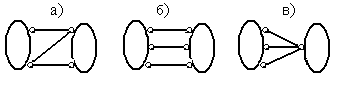
Рис.1.13
2) Шарнирный треугольник является геометрически неизменяемой системой, а шарнирный четырехугольник – геометрически изменяемой. Поэтому всякая сложная система, составленная из шарнирных треугольников, является геометрически неизменяемой, а система, содержащая шарнирный четырехугольник, является геометрически изменяемой. На рис.1.14,а показан пример геометрически неизменяемой системы, а на рис.1.14,б пример геометрически изменяемой системы.
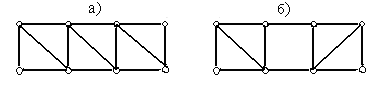
Рис.1.14
3) Сплошной или решетчатый диск на плоскости, закрепленный с помощью трех опорных связей является неподвижным, если указанные связи не параллельны между собой и не пересекаются в одной точке. На рис.1.15,а показана неподвижная система, а на рис.1.15,б и 1.15,в) – подвижные системы.

Рис.1.15
Статический метод исследования геометрической неизменяемости и неподвижности стержневых систем состоит в определении реактивных сил сопротивления, возникающих в связях от любых нагрузок. Если эти силы сопротивления имеют единственные определенные и конечные значения, то исследуемая стержневая система геометрически неизменяемая или неподвижна. Если же указанные силы сопротивления принимают неопределенные или бесконечные значения, то исследуемая система геометрически изменяемая или подвижна.
При исследовании стержневой системы статическим методом не всегда следует определять реакции связей. Если из условий равновесия составлена система уравнений и определитель этой системы не равен нулю, то такая система является геометрически неизменяемой или неподвижной.
На рис.1.16 показано тело, шарнирно закрепленное двумя стержнями и загруженное вертикальной силой. От действия этой силы в стержнях возникнут продольные усилия 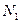 и
и 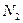 .
.
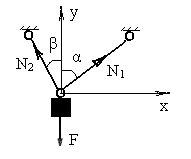
Рис.1.16
Для определения этих усилий составляем два уравнения из условий равновесия загруженного тела:
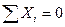 и
и 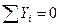
Получаем систему уравнений равновесия:
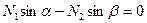
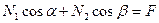
Составим определитель этой системы, раскроем его и установим, в каких случая он может быть равным нулю (только в этих случаях усилия могут принимать неопределенные либо бесконечные значения).
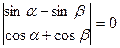 , откуда
, откуда 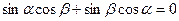
Или 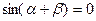 . Это равенство возможно в двух случаях: 1) когда
. Это равенство возможно в двух случаях: 1) когда 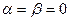 , т.е. когда стержни совмещаются и образуют мгновенно изменяемую систему; 2) когда
, т.е. когда стержни совмещаются и образуют мгновенно изменяемую систему; 2) когда 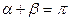 , т.е. когда стержни располагаются на одной горизонтальной или наклонной прямой и также образуют мгновенно изменяемую систему. Во всех иных случаях рассматриваемая стержневая система неподвижна и способна удерживать заданную нагрузку.
, т.е. когда стержни располагаются на одной горизонтальной или наклонной прямой и также образуют мгновенно изменяемую систему. Во всех иных случаях рассматриваемая стержневая система неподвижна и способна удерживать заданную нагрузку.
Следует иметь в виду, что статический метод всегда позволяет получить точный ответ на вопрос является ли исследуемая система геометрически неизменяемой или неподвижной, либо относится к другой категории.
1.5 Классификация стержневых систем, нагрузок и состояний.
Все стержневые системы делятся на плоские и пространственные. В плоских системах все стержни и их связи располагаются в одной плоскости, а в пространственных системах они располагаются в разных плоскостях. На рис.1.17,а показана расчетная схема простой пространственной рамы, а на рис.1.17,б – расчетная схема одноэтажной двухпролетной плоской рамы.
Плоские и пространственные системы в свою очередь делятся на статически определимые и статически неопределимые. Реакции опорных связей и внутренние усилия в элементах статически определимых систем вычисляются по методам равновесия дисков или узлов. Реакции опорных связей и внутренние усилия в элементах статически неопределимых систем вычисляются с использованием специальных методов расчета таких систем. В дальнейшем будут рассмотрены два основных метода определения усилий в статически неопределимых системах: метод сил и метод перемещений.
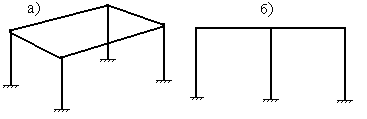
Рис.1.17
Плоские и пространственные системы могут быть сплошными, решетчатыми и комбинированными. Сплошные системы образуются по первому варианту, решетчатые системы образуются по второму варианту, а комбинированные системы образуются по двум вариантам одновременно в разных частях.
К сплошным системам относятся различного рода балки (статически определимые и статически неопределимыеого рода балки ()ыть сосредоточенными, распределенными или моментными. ых методов их расчета.
не, так ), трехшарнирные арки и рамы, многошарнирные и бесшарнирные рамы.
К решетчатым системам относятся плоские и пространственные, статически определимые и статически неопределимые фермы.
К комбинированным системам относятся висячие и шпренгельные системы.
Нагрузки, действующие на стержневые системы, делятся на два класса: статические и динамические. Статические нагрузки нарастают постепенно и не приводят к появлению сил инерции масс системы, а динамические нагрузки непрерывно меняются во времени как по величине, так и по направлению, вызывая при этом появление дополнительных сил инерции масс системы. Такое коренное различие между нагрузками приводит к необходимости разработки и применения различных методов их расчета.
Статические и динамические нагрузки могут быть сосредоточенными, распределенными или моментными. Такое деление нагрузок не приводит к необходимости создания различных методов расчета стержневых систем.
В процессе эксплуатации элементы стержневых систем проходят различные стадии напряженно деформированных состояний в зависимости от возможных изменений действующих нагрузок и условий эксплуатации. Главными из них являются два состояния: эксплуатационное состояние и предельное состояние системы.
Эксплуатационное состояние характеризуется проектными величинами усилий, напряжений и деформаций, которые определяют несущую способность сооружения.
Предельное состояние системы может наступить при появлении дополнительных нагрузок, не предусмотренных проектом. Например, при действии на сооружение землетрясения, урагана, морских волн (цунами). В предельном состоянии системы возникают предельные усилия, напряжения и деформации, которые приводят к разрушению зданий и сооружений.
Вопросы для самоконтроля полученных знаний.
1. Что такое строительная механика и в чем ее отличие от сопротивления материалов и других смежных дисциплин?
2. Что характерно для развития строительной механики на современном этапе?
3. Какова задача строительной механики и в чем ее важность?
4. Что такое расчетная схема сооружения? Какими соображениями руководствуются при ее выборе?
5. Из каких элементов может быть составлено сооружение?
6. Как соединяются между собой отдельные стержни плоского сооружения?
7. Как различаются сооружения в зависимости от способов соединения стержней?
8. Что такое кратный шарнир?
9. Назовите виды опор плоских сооружений. Каковы их кинематические и статические свойства?
10. Приведите классификацию нагрузок. Какие другие воздействия может испытывать сооружение?
11. Что называют числом степеней свободы сооружения?
12. Как определить количество связей в соединении дисков или в опоре?
13. Как геометрическая неизменяемость сооружения связана с числом степеней свободы?
14. Какая система называется статически определимой?
15. Как статическая определимость сооружения связана с числом степеней свободы?
16. В каком случае и почему для проверки геометрической неизменяемости сооружения необходимо выполнить анализ его геометрической структуры
17. Перечислите основные способы образования геометрически неизменяемых систем.
18. Какие системы называют мгновение изменяемыми?
19. Почему мгновенно изменяемые системы не применяют в сооружениях?
20. Каковы статические признаки мгновенной изменяемости сооружения?
21. Какие допущения о свойствах материалов принимают в строительной механике?
22. Какие системы называют линейно деформируемыми? Каковы следствия допущения о линейной деформируемости системы?
23. В каком случае можно выполнять расчет сооружения по недеформируемой схеме?
Дата: 2019-02-02, просмотров: 428.