 |
Почему же в промежуточных реакциях могут быть более высокие константы скорости? Прежде чем ответить на этот вопрос, для произвольной двусубстратной реакции вида
| |
запишем уравнение скорости, используя формулу Эйринга (18.40):
Отсюда можно сформулировать три принципиальных способа ускорения реакций
1. Первый из них — увеличение эффективной концентрации реагентов.
а) Данный механизм явно отсутствует в приведенных двух примерах катализа низкомолекулярными веществами (ионами Fe2+ и молекулами I2).
Но он может играть важную роль, когда поверхность катализатора достаточно велика и на ней предварительно связываются молекулы реагентов. Такая ситуация имеет место при гетерогенном катализе, а также при ферментативном катализе, осуществляемом макромолекулами (каковыми являются белки).
в) Так вот, при связывании молекул реагентов с катализатором могут происходить их сильное сближение друг с другом и правильная ориентация друг относительно друга, что и означает повышение эффективной концентрации.
2. Второй принципиальный способ ускорения касается энергии активации.
 |
а) Вспомним её определение (п. 18.2):
т.е. это разница между средней и барьерной (в отношении реакционной активности) энергией вещества.
б) Отсюда второй способ ускорения — это уменьшение энергии активации
«снизу», т.е. за счет увеличения средней энергии реагентов (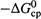 
; рис. 20.1).
Этот способ тоже возможен лишь в случае катализаторов с достаточно
большой поверхностью (ферменты; гетерогенный катализ).
в) Можно представить, что связывание реагента с катализатором сопровождается созданием напряжения в молекуле реагента. Из-за взаимодействия с химическими группами катализатора, определенная связь в реагенте как бы растягивается» (ослабевает), что означает переход реагента в возбуждённое состояние.
г) Когда же превращение молекулы реагента в продукт завершается, часть высвобождающейся в реакции энергии идёт на восстановление прежней структуры катализатора. Таким образом, повышение энергии реагента катализатором совершается как бы «в долг» – в счёт части энергии последующей реакции.
 |
3. а) И, наконец, третий способ ускорения — уменьшение энергии активации «сверху», т.е. путем снижения энергетического барьера (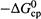 
; рис. 20.2).
б) Этого можно достичь путем разбиения исходной реакции на несколько других с меньшими значениями барьерной энергии.
 |
Действительно, допустим, что реакция (20.23) заменяется на две другие:
Если соответствующие группы катализатора уже находятся в реакционно-
активном состоянии, то на первой стадии необходимо активирование лишь
реагента S1, а на второй — реагента S2.
в) В исходной же реакции требуется одновременная активация сразу обоих реагентов. Следовательно, энергия активации каждой промежуточной реакции ниже (за счет более низкого барьера) энергии активации исходной реакции. И наиболее высокое из этих небольших значений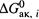 
определяет константу скорости результирующего превращения.
г) Очевидно, именно данный способ реализуется при катализе неорганическими веществами. В случае же ферментов могут использоваться все три способа (хотя, конечно, не обязательно, что все способы — сразу).
4. Продемонстрируем, насколько эффективно влияет снижение ∆G0ак на константу скорости. Пусть под влиянием катализатора ∆G0ак уменьшается от 109 кДж/моль до 74,5 кДж/моль.
 |
Тогда, согласно формуле Эйринга (18.44), при t = 37°С
т.е. скорость реакции увеличивается в миллион раз.
Уравнение Михаэлиса-Ментен
Теперь обратимся к кинетике каталитических реакций. Для определенности, будем иметь в виду ферментативные реакции, хотя многое из нижеследующего справедливо и для прочих каталитических процессов.
 |
1. Как и для цепных реакций, уравнение скорости ферментативного процесса зависит от его конкретного механизма. Рассмотрим простейший случай: односубстратныв необратимые реакции вида
протекающие в две стадии:
 |
На первой (обратимой) стадии образуется фермент-субстратный комплекс ES , а на второй он необратимо распадается на фермент и продукт реакции.
2. Вывод уравнения скорости производится по тому же принципу, что и для
цепных реакций (п. 20.2).
а) Так, тоже исходят из условия стационарности. В данном случае оно означает постоянство концентрации комплекса ES :
 |
б) Заметим, что концентрация свободного фермента равна
 |
где c E,0 — общая концентрация фермента — и в свободном состоянии, и в составе комплекса ES .
 |
в) Подставляя c E в (20.29), можно найти стационарную концентрацию комплекса:
 |
Здесь введена константа Михаэлиса:
 |
г) Скорость же образования конечного продукта, а значит и скорость реакции в целом, очевидно, такова:
 |
д) Подставляя c ES, получаем искомое выражение:
Величина Vmax — это максимальная скорость реакции; формула же (20.34, а) — уравнение Михаэлиса—Ментен, являющееся основным в ферментативной кинетике.
3. Проанализируем это уравнение.
 |
а) При малых концентрациях субстрата S (когда c S « KM) имеем:
т.е. фермент работает в линейном режиме, а реакция имеет первый порядок.
б) Если же, напротив, концентрация субстрата очень велика, получаем режим насыщения:
Здесь скорость перестает зависеть от концентрации субстрата, не поднимаясь выше Vmax, т.е. реакция приобретает нулевой порядок.
в) Отсюда — та гипербола, которой описывается зависимость v от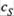 
для ферментативной реакции (рис. 20.3). По мере же расходования субстрата порядок реакции изменяется от нулевого до первого.
Дата: 2019-02-02, просмотров: 274.
