Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Сделаем еще несколько замечаний по поводу основного уравнения фер-
ментативной кинетики.

1. Параметры уравнения — V_max и K_M.

а) Смысл величины V_max  мы уже отмечали.

Это максимальная скорость, достигаемая при насыщающих концентрациях
субстрата. Согласно (20.34,б) и (20.39,б),

т.е. V_max зависит от концентрации фермента и максимального числа оборотов отдельных молекул фермента.

б) Смысл K_M таков.

I . Положим c_S = K_M; тогда из уравнения (20.34, а) вытекает:

 

Следовательно, K_M — такая концентрация субстрата, при которой достигается скорость реакции, равная половине максимальной.

II . Несколько упрощая, можно сказать, что K _M отражает сродство фермента к
субстрату: чем это сродство выше, тем K_M меньше, т.е. тем круче идет кривая
зависимости υ от c _S на рис. 20.3.

в) Итак, K_M  характеризует сродство фермента к субстрату, а V_max — активность фермента, уже связавшего субстрат.

2. Определение  V_max и K_M.

а) Эти параметры обычно определяют экспериментальным путем, для чего измеряют скорость реакции при разных концентрациях субстрата.

б) Но непосредственно по графику υ(c _S) трудно заключить, чему равна V_max: не всегда ясно, к какому пределу стремится кривая. Поэтому преобразовывают уравнение Михаэлиса—Ментен к линейной форме.

в) Наиболее часто используется метод Лануйивера—Берка (или метод обратных величин):

Здесь получается линейная зависимость 1/υ от 1/c _S.

г) Итак, по экспериментальным данным строят график для обратных величин (рис. 20.4). И, продолжая его, находят точки пересечения с осями координат. Как видно из рис. 20.4, эти точки отсекают на оси абсцисс величину –1/K_M, а на оси ординат – 1/V_max.

3. Решение уравнения Михаэлиса–Ментен.

а) Если учесть, что

то уравнение Михаэлиса–Ментен — это дифференциальное уравнение относительно c _S:

 

б) Здесь можно разделить переменные и проинтегрировать:

откуда

 

Два первых члена правой части — это постоянная интегрирования, опре-
деляемая из начального условия (при t = 0 c _S = 0).

в) Но полученное алгебраическое уравнение является трансцендентным, и в явном виде выразить из него 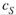нельзя. Тем не менее, видно, что при росте t c _S уменьшается, что примерно отражается графиком на рис. 20.5. Начальная часть графика близка к линейной зависимости {нулевой порядок реакции), а
конечная — к экспоненциальной {первый порядок).

 

Краткое содержание главы 20

 

В главе рассмотрены цепные и каталитические реакции.

1. а) Особенностью ЦЕПНЫХ реакций является то, что среди их продуктов образуются СВОБОДНЫЕ РАДИКАЛЫ, которые вовлекают в процесс новые молекулы реагентов.

В самом процессе различают три стадии – зарождение, продолжение и обрыв цепи. Стадия продолжения состоит из повторяющихся циклов реакций (т.н. звеньев), инициирующих друг друга.

б) Были приведены примеры цепных реакций, в т.ч.:

в) Кинетические уравнения скорости зависят от механизма цепного процесса. В частности, для первой из приведенных реакций уравнение таково:

 

По мере расходования брома порядок реакции по нему возрастает от 1/2 до 3/2.

 

2. а) Что касается КАТАЛИТИЧЕСКИХ процессов, то даны краткие представления о ПОЛОЖИТЕЛЬНОМ и отрицательном, ГОМОГЕННОМ и ГЕТЕРОГЕННОМ катализе, АВТОКАТАЛИТИЧЕСКИХ процессах, ФЕРМЕНТАХ – биологических катализаторах белковой природы.

б) Принципиальная особенность катализа состоит в том, что катализатор не входит в суммарное уравнение реакции и увеличивает в равной степени скорость как прямой, так и обратной реакции.

в) Возможные способы действия катализаторов таковы:

- увеличение эффективной концентрации реагентов,

- повышение энергии реагентов (создание напряжения в их молекулах),

- понижение энергетического барьера (путём разбиения исходной реакции на промежуточные стадии с меньшими барьерами).

г) Для ферментативных реакций, протекающих по простейшему механизму:

скорость описывается УРАВНЕНИЕМ МИХАЭЛИСА-МЕНТЕН:

 

д) При этом КОНСТАНТА МИХАЭЛИСА, К_М , численно равна концентрации субстрата, при которой скорость реакции составляет половину максимальной (0,5 V_max).

Значения параметров К_М  и V_max  можно определить по графику зависимости  1/ v от 1/ c_S  (метод Лануйивера-Берка).

е) Интегрирование же уравнения Михаэлиса-Ментен приводит к трансцендентному алгебраическому уравнению относительно концентрации субстрата:

                                     c_S + K_M∙ ln c_S = c^o_S + K_M∙ ln c^o_S – V_max .

 

Глава 21. КИНЕТИКА ГЕТЕРОГЕННЫХ ПРОЦЕССОВ

 

Введение

До сих пор речь шла о кинетике лишь гомогенных процессов.

1. Теперь же обратимся к гетерогенным процессам, где реагирующие вещества находятся в разных фазах. Следовательно, в таких процессах реакция происходит на границах раздела фаз.

2. Конкретным примером являются электродные процессы (главы 14–15) —
электролиз и генерация ЭДС в гальванических элементах.

В частности, возьмем элемент из двух редокс-электродов (рис.14.3).
В левом полуэлементе взаимодействуют растворенное вещество AH₂ и платина в составе твердого электрода: эти вещества обмениваются электронами.

Очевидно, сама полуреакция происходит на поверхности электрода.
То же можно сказать о правом полуэлементе.

3. Реакции на границе раздела фаз имеют определенные особенности кинетики. Эти особенности мы обсудим вначале с общих позиций (т.е. применительно к любым гетерогенным процессам), а в следующей главе — в отношении конкретных электрохимических процессов.

а) В гетерогенной реакции различают обычно не менее трех стадий:

I. перенос реагирующих веществ к поверхности раздела фаз,

II. собственно реакцию,

III. отвод продуктов реакции от поверхности.

б) Причём в основе первой и третьей стадий лежат не химические, а физико-химические процессы. Как правило, это диффузия и движение частиц в электрическом поле.

4. В частности, для приведенного выше примера стадии левой полуреакции отражаются схемой:

5. а) Результирующая же скорость гетерогенной реакции определяется, очевидно, самой медленной стадией. Чаще всего такой стадией является именно диффузия.

б) Следовательно, диффузия играет очень важную роль в кинетике гетерогенных процессов. В связи с этим, остановимся на ней подробнее.

Общие сведения о диффузии

1. а)Диффузия — это самопроизвольное перемещение частиц {молекул) из области с более высокой в область с более низкой концентрацией. В основе ее — хаотичное тепловое движение данных частиц.

б) В п. 4.8 мы давали практически такое же определение для осмотических
процессов. И находили, что при переходе п молей вещества от концентрации c₁
 к меньшей концентрации c₂ уменьшение энергии Гиббса системы равно

 

в) Отсюда следуют два обстоятельства.

I . Во-первых, диффузия — это те же осмотические процессы, но рассматриваемые на уровне частиц и молекул.

II . Во-вторых, в результате диффузии, как и в осмотических процессах, теплота не поглощается и не выделяется, а все изменение ∆G обусловлено изменением только энтропии системы.

г) Причем, видимо, в ходе диффузии энтропия возрастает, т.к. частицы переходят к менее упорядоченному расположению. Таким образом, диффузия — одно из проявлений второго начала термодинамики.

2. а) Важнейшей характеристикой является поток диффузии в каком-либо на-
правлении, j_диф. Это количество вещества (в молях), диффундирующего в единицу времени через единичное поперечное сечение, перпендикулярное данному направлению:

 

3. Для диффузии характерны следующие три закона.

I . Первый закон Фика (в одномерном варианте):

 

а) Суть этого закона в том, что поток диффузии в определенном направлении
пропорционален градиенту концентрации вещества в данном направлении.

Иными словами, чем больше разница концентраций между точками пространства, тем сильней диффузия.

б) Знак минус в формуле (21.2, а) обусловлен тем, что диффузия происходит в сторону снижения градиента концентрации (дс/д x < 0), тогда как величина j_диф должна быть положительной.

в) Что касается D , то это — коэффициент диффузии.

II . Второе соотношение — уравнение непрерывности:

а) Чтобы понять его, выделим на направлении диффузии небольшой интервал dx , ограниченный сечениями I и II (рис. 21.2).

Ввиду малости интервала можно полагать, что во
всех его точках концентрация одинакова и равна с.

б) Так вот, уравнение (21.3) констатирует довольно очевидную вещь.

Концентрация вещества в интервале dx изменяется со временем (д c /д t ≠ 0) в том случае, если на границах этого интервала различен диффузионный поток (д j_диф /д x ≠ 0).

в) Действительно, чтобы, например, концентрация убывала со временем, необходимо, чтобы приток вещества в интервал был меньше оттока вещества из интервала:

 

г) Таким образом, положительный градиент потока диффузии (∂ j_диф/∂х > 0) вызывает снижение концентрации в точках интервала (∂с/∂ t < 0), а отрицательный градиент потока – возрастание концентрации.

III . Наконец, третье соотношение — второй закон Фика. Он следует из первых двух законов, если коэффициент диффузии одинаков во всех точках пространства:

откуда

б) Итак, скорость изменения со временем концентрации вещества в некоторой точ ке пространства пропорциональна второй производной концентрации вещества по направлению диффузии.

4. Завершая краткое изложение сведений о диффузии, отметим также свойст-
ва стационарной диффузии.

а) Диффузия называется стационарной, если концентрация вещества в точках пространства, несмотря на диффузию, не меняется:

 

б) Исходя из законов диффузии, можно установить ещё три признака стационарной диффузии.

I . Первый признак. Так, из второго закона Фика следует: если д c /д t = 0, то

 

Иначе говоря, убывание концентрации по направлению диффузии происходит линейно.

II . Второй признак. Из уравнения непрерывности получаем: если д c /д t = 0, то

III . Третий признак. И, наконец, используем первый закон Фика:

 

Два последних свойства означают: при стационарной диффузии поток диффузии не меняется ни со временем, ни по мере перехода от одной точки пространства к другой.