Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Такие реакции могут быть одно- и двусубстратными.

1. Односубстратные реакции.

а-б) В этом случае реагируют две молекулы одного вещества:

 

 

Записано и дифференциальное уравнение скорости (где с — концентрация
вещества А). Теперь скорость зависит уже от второй степени концентрации.

в) I . Разделяем переменные и интегрируем:

 

II. Из начального условия (при t = 0   с = с⁰) следует:

III . Отсюда — линейная форма интегрального уравнения:

т.е. здесь зависимость является линейной в координатах время — обратная концентрация.

г) Поскольку сама концентрация со временем убывает, то обратная величина
увеличивается (рис. 17.5). В явном же виде зависимость c ( t ), как нетрудно
найти, такова:

По сравнению с экспоненциальным снижением концентрации в реакциях
первого порядка, здесь уменьшение концентрации (при том же численном
значении k) происходит более плавно (рис. 17.6).

д) Период полупревращения —

 

Как видим, этот период зависит от того, какую концентрацию вещества А
мы выбираем за начальную: чем меньше концентрация, тем больше период
полупревращения.

2. Двусубстратные реакции:

а) Если начальные концентрации реагентов одинаковы ( 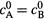), то, очевидно, в любой момент будут равны и текущие концентрации веществ (c_A = c_B). Тогда уравнение скорости сводится к предыдущему (17.22,б). И мы получим для концентрации каждого из двух реагентов те же самые формулы (17.25—17.26).

б) В общем же случае начальные концентрации различны. Но убыль обоих веществ за некоторое произвольное время одинакова.

I . Поэтому можно выразить c_B через c_A и через начальные концентрации (считающиеся известными):

II. Подставляя в (17.28,б), получаем дифференциальное уравнение относительно c_A:

 

III . Для его решения надо сделать замену:

откуда

 

IV . Подстановка в уравнение (17.30) дает:

 

или

 

V . Получили уравнение, аналогичное уравнению (17.13, г). Соответственно, решение тождественно формуле (17.16):

 

VI . Тогда для обратной величины (концентрации вещества А) приходим, с учетом вида а и b , к такому выражению:

или

 

в) Пусть, для определенности, 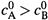. Тогда экспонента в знаменателе формулы (17.35) — убывающая, и

 

I . Следовательно, данная формула описывает убывание концентрации вещества А до того, пока не
израсходуется вещество В (рис. 17.7). Такой график
был приведен в п. 16.4 (рис. 16.1,б). Теперь получена
конкретная математическая формула, описывающая ход кривой. .

II . Нетрудно убедиться, что падение концентрации второго вещества (В) будет описываться в этом случае ( 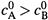) параллельной кривой, лежащей ниже первой на расстоянии  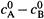 и потому стремящейся к нулю.

г) Период полупревращения в том же случае ( 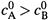) находим, полагая в левой части формулы (17.35), что

 

Решая уравнение относительно времени, находим:

 

Одновременно это период полуисчезновения вещества В.