Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

и давле­нию

Выше шла речь об энергии Гиббса применительно только к изотермо- изобарным процессам в закрытых системах, где данная функция является термодинамическим потенциалом.

Однако величину ΔG можно рассматривать в любом процессе. От каких параметров и как тогда она зависит?

а) Согласно определению (4.7, а),

 

б) Отсюда изменение энергии Гиббса на микростадии произвольного процес­са таково:

 

в) Пусть процесс является обратимым (т. е. на каждой микростадии система находится в состоянии равновесия) и пусть возможная работа совершается только против давления. Тогда, в соответствии с (1.7) и (3.4),

 

 

г) С учетом этого в выражении (4.17,б) три подчеркнутые члена сокращаются, давая в сумме ноль. Остается следующее:

 

Отсюда вывод: энергия Гиббса равновесного процесса (и равновесной системы) зависит от двух независимых переменных — давления и температуры (чего, в общем, и следовало ожидать).

д) Соответствующие частные производные таковы:

 

 

 

т.е. температурная зависимость энергии Гиббса определяется энтропией си­стемы, а зависимость от давления — объемом системы.

 

Химический потенциал

1. а) Как известно, в химических процессах меняется и количество того или иного вещества. Поэтому энергия Гиббса системы в состоянии равновесия зависит также от количества ее компонентов:

 

Это означает, что выражение (4.19) следует расширить, добавляя члены, содержащие дифференциалы n_i :

 

 

б) Множители  μ_j  при данных дифференциалах называются химическими потенциалами компонентов системы.

Очевидно, каждый такой множитель — это частная производная энергии Гиббса по количеству соответствующего вещества:

2. а) Если условия являются изотермо-изобарными (т.е. когда dP = dT = 0), выражение (4.21,б) сводится к сумме парциальных энергий Гиббса, относя­щихся к отдельным химическим компонентам системы:

 

б) Отсюда вытекает простая интерпретация химического потенциала того или иного компонента. По существу, μ _j — это та часть энергии Гиббса системы, которая приходится на 1 моль данного вещества, т. е. это просто энергия Гиббса 1 моля вещества.

в) Следовательно, для изотермо-изобарных процессов химический потенци­ал компонента системы можно отождествлять с его молярной энергией Гиббса, а так как зависимость G_j от числа молей — линейная, то можно просто написать:

3. Соответственно, для изотермо-изохорного процесса

 

 

т. е. здесь 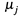— это энергия Гельмгольца 1 моля вещества.

Вышесказанное применимо и к физическим, и к химическим процессам. Далее же будет рассмотрена энергия Гиббса преимущественно химических систем, для которых мы получим ряд полезных соотношений.

Однако предварительно необходимо остановиться на осмотических про­цессах, поскольку химическую систему можно представить как совокупность осмотических систем.

 

Осмотические процессы

1. а) В осмотическом процессе все изменение системы состоит в изменении концентрации растворенного вещества.

б) В п. 3.4 отмечалось, что в таком процессе (в изотермических условиях) теплота не поглощается и не выделяется. Как там было сказано, разбавление раствора эквивалентно расширению газа в пустоту, а при таком расширении работа против давления не совершается, отчего не требуется и поглощение теплоты.

в) Итак, первое слагаемое энергии Гиббса равно нулю, и все изменение этой энергии обусловлено только изменением энтропии системы:

 

г) В том же п. 3.4 указано, что изменение энтропии в таких процессах рассчиты­вается (при не очень больших концентрациях) по формуле:

 

 

д) Подставляя это выражение в (4.26, б), получаем и формулу для расчета энергии Гиббса:

 

2. а) Обе эти формулы имеют строго определенную область применимости и относятся к переходу п молей вещества от концентрации 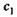к концентрации .

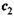Указанный переход может совершаться в следующих случаях:

I . при разбавлении или концентрировании вещества путем изменения
содержания растворителя,

II . в ходе переноса вещества через границу, разделяющую две среды с разными и постоянными концентрациями этого вещества (рис. 4.2).

б) Второй случай особо важен для биологических объектов — это, по суще­ству, трансмембранный транспорт веществ. А чтобы концентрации в отсеках оставались постоянными, отсеки надо считать неогра­ниченными. При этом совокупность растворенного ве­щества в обоих отсеках — закрытая система, так что критерием самопроизвольности переноса веществ через границу, действительно, является энергия Гиббса (при Т и Р – const).

3. Формула (4.27) показывает:

 

 

т.е. самопроизвольным может быть только переход вещества от состояния с большей концентрацией в состояние с меньшей концентрацией.