Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

термоди­намики

Согласно п. 3.1, термодинамическая осуществимость процесса определяется балансом двух критериев: теплоты процесса и изменения энтропии.

1. а) С учетом того, что энтропия имеет размер приведенной теплоты, для бес­конечно малой стадии процесса данное утверждение записывают так:

Это означает, что процесс может идти только в том случае, если величина слева — отрицательна или равна нулю.

б) Если теплота выделяется, то 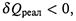что дает отрицательный вклад в баланс.

Аналогично, если энтропия увеличивается, то –T dS тоже меньше 0 (поэтому член T dS взят с обратным знаком). Оба эти изменения способствуют протеканию процесса.

в) Выше говорилось, что процесс может идти за счет и лишь одного стимула, если он «перевешивает» неблагоприятное воздействие второго критерия.

г) Поскольку 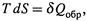 то второе начало термодинамики можно записать и так:

 

 

Следовательно, с учетом знака теплота реального процесса — не больше теплоты обратимого процесса, связывающего те же состояния системы.

2. Кроме того, можно объединить первое и второе начала термодинамики в одном выражении.

а) Запишем первое начало (1.7) в дифференциальной форме:

выразим отсюда 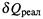и подставим в неравенство второго начала (3.31):

Это – так называемое основное неравенство термодинамики, объединяющее оба ее начала.

б) Из последнего неравенства, в частности, следует, какую предельную по величине работу может совершить система в процессе:

 

(Поскольку работа совершается системой, то 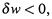так что слева — положительная величина.)

3. Нередко утверждают, что существование энтропийного фактора ограничивает возможность системы совершать работу.

а) В общем случае это неверно. Как видно из соотношения (3.35), если dS >0 (энтропия возрастает), то справа оказывается бóльшая величина, т.е. повышается верхний предел работы.

б) Действительно, в процессах жизнедеятельности работа часто совершается за счет только градиента концентраций; происхождение энергии здесь целиком обусловлено энтропийным фактором: внутренняя энергия при выравнивании концентраций разбавленных растворов не меняется.

4. а) В тепловых же машинах, с анализа которых зародилась термодинамика, происходит циклический процесс (как было показано на примере цикла Карно; п.3.2). Причём работа совершается за счёт подводимой извне теплоты (Q₁), часть которой (Q₂) отдаётся системой холодильнику.

б) Ранее (см. (3.8,а)) было найдено, что

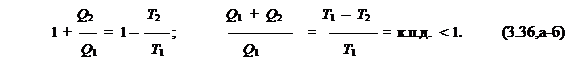Перевернём это равенство и прибавим к каждой его части единицу. Тогда получим:

Здесь учтено, что, в соответствии с (3.6,а-б),

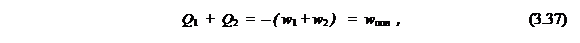где w _пол – результирующая полезная работа, совершённая машиной, а отношение w _пол к полученной теплоте (Q ₁ ) есть коэффициент полезного действия.

в) Неравенство к.п.д. < 1  следует из предположения, что абсолютный нуль температуры недостижим (т.е. Т₂ ≠ 0 ).

Действительно, из последнего вытекает, что в тепловой машине даже в обратимом процессе всё получаемое извне тепло трансформироваться в работу не может (что и означает: к.п.д. тепловой машины – меньше единицы).

г) Обычно это утверждение и выражающее его соотношение (3.36) рассматривают как одну из формулировок второго начала термодинамики. Однако суть такого постулата узка и специфична: она справедлива лишь для тепловых машин.

 

Краткое содержание главы 3

 

1. В главе дано определение ВТОРОГО НАЧАЛА ТЕРМОДИНАМИКИ: имеются ДВА СТИМУЛА для самопроизвольного изменения термодинамической системы – I.ВЫДЕЛЕНИЕ ТЕПЛОТЫ и II.УВЕЛИЧЕНИЕ ЭНТРОПИИ. Результирующий же критерий, определяющий возможность процесса, есть баланс действия данных стимулов.

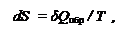2. Фигурирующая здесь ЭНТРОПИЯ – это мера энергетического беспорядка в системе. Но практические её расчёты основаны на соотношении

которое утверждает, что изменение энтропии в любом реальном процессе измеряется приведённой теплотой обратимого процесса, связывающего те же состояния системы.

3. Для доказательства того, что δQ_обр/ T –  ФУНКЦИЯ СОСТОЯНИЯ, был рассмотрен цикл Карно.

4. Получен ряд формул расчёта  Δ S и S .

I. Нагревание системы:

 

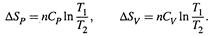
II. Абсолютная энтропия:

 

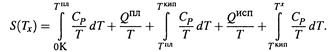
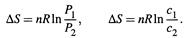III. Изотермическое расширение газа и изотермическое изменение концентрации раствора:

 

 

5. Рассмотрена также статистическая природа энтропии. Энтропия определяется через ВЕРОЯТНОСТЬ МИКРОСОСТОЯНИЙ (р_i) или (при равенстве р_i) через ЧИСЛО МИКРОСОСТОЯНИЙ (Ω = 1/ p ):

 

 

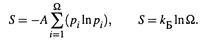
6. Дана также математическая формулировка второго начала термодинамики:

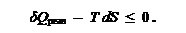Это – запись утверждения о том, что термодинамическая возможность процесса определяется балансом двух критериев – теплоты и изменения энтропии.