Числовой последовательностью называется занумерованное множество чисел, расположенных в порядке возрастания номеров.
В общем виде записывают: 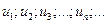 , где
, где 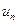 называется общим членом последовательности.
называется общим членом последовательности.
Последовательность 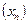 называется возрастающей,( убывающей) если каждый ее член начиная со второго, больше (больше или равен) предыдущего, т.е. если для любого n выполняется неравенство:
называется возрастающей,( убывающей) если каждый ее член начиная со второго, больше (больше или равен) предыдущего, т.е. если для любого n выполняется неравенство: 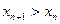 .(
.( 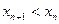 )
)
Переменная величина 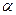 называется бесконечно малой, если она изменяется так, что, какое бы малое положительное число
называется бесконечно малой, если она изменяется так, что, какое бы малое положительное число 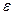 ни взять, абсолютная величина
ни взять, абсолютная величина 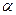 становится, и, при дальнейшем изменении величины
становится, и, при дальнейшем изменении величины 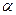 , остается, меньше
, остается, меньше 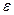 .
.
Если 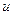 - бесконечно большая величина, то обратная ей величина
- бесконечно большая величина, то обратная ей величина 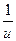 будет бесконечно малой.
будет бесконечно малой.
Если 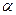 - бесконечно малая величина, то обратная ей величина
- бесконечно малая величина, то обратная ей величина 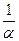 будет бесконечно большой.
будет бесконечно большой.
Постоянная 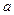 называется пределом переменной х , если х в некотором процессе стремится к конечному пределу и безгранично приближается к
называется пределом переменной х , если х в некотором процессе стремится к конечному пределу и безгранично приближается к 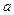 . Тогда пишут
. Тогда пишут 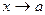 или
или 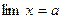 .
.
Число 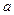 называется пределом последовательности
называется пределом последовательности 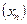 , если для любого положительного числа
, если для любого положительного числа 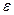 можно подобрать такой номер N0, что начиная с этого номера ( т.е. для всех n
можно подобрать такой номер N0, что начиная с этого номера ( т.е. для всех n 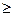 N0), будет выполнено неравенство:
N0), будет выполнено неравенство: 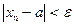
( 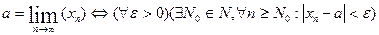 )
)
Если последовательность имеет конечный предел, то она называется сходящейся, если не имеет конечного предела, тогда расходящейся.
Свойства пределов:
1. Если последовательность имеет конечный предел, то только один.
2. Предел постоянной величины равен ей самой: 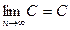
3. Предел суммы (разности) двух сходящихся последовательностей равен сумме (разности) их пределов: 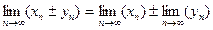 .
.
4. Предел произведения двух сходящихся последовательностей равен произведению их пределов: 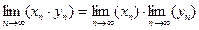
5. Постоянный множитель можно выносить за знак предела: 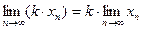 (
( 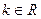 )
)
6. Предел частного двух сходящихся последовательностей равен частному их пределов:
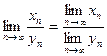 (
( 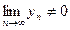 )
)
7. Предел корня k-ой степени от сходящейся последовате6льности равен корню этой же степени от предела последовательности: 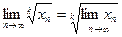
Важно знать некоторые пределы:
1. 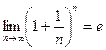 , где
, где 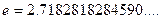 - второй замечательный предел
- второй замечательный предел
2. 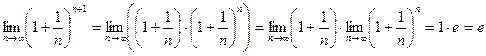
3. 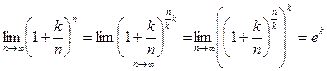
Определение предела функции по Гейне:
Число А называется пределом функции 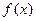 при
при 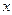 стремящимся к
стремящимся к 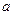 , если для любой последовательности
, если для любой последовательности 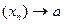 , все члены которой принадлежат области определения функции
, все члены которой принадлежат области определения функции 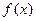 и не равны
и не равны 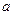 выполняется условие что последовательность
выполняется условие что последовательность 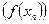 стремится к А.
стремится к А.
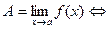
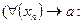
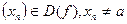 )
) 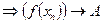
Определение предела функции по Коши:
Число А называется пределом функции 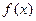 при
при 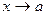 , если для любого числа
, если для любого числа 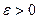 можно указать такое
можно указать такое 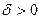 , что для всех
, что для всех 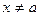 , удовлетворяющего неравенству
, удовлетворяющего неравенству 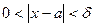 , выполняется неравенство
, выполняется неравенство 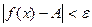 .
.
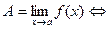
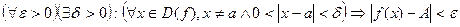
В этом случае пишут 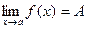 .
.
Если число А1 есть предел функции 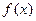 при х, стремящемся к а, так, что х принимает только значения, меньшие а, то А1 называется левым пределом функции
при х, стремящемся к а, так, что х принимает только значения, меньшие а, то А1 называется левым пределом функции 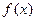 в точке а. При этом пишут
в точке а. При этом пишут 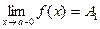 .
.
Если число А2 есть предел функции 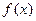 при х, стремящемся к а, так, что х принимает только значения, большие а, то А2 называется правым пределом функции
при х, стремящемся к а, так, что х принимает только значения, большие а, то А2 называется правым пределом функции 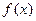 в точке а. При этом пишут
в точке а. При этом пишут 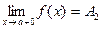 .
.
Эти пределы называются односторонними пределами функции.
Теорема: Для того, чтобы функция 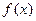 имела предел равный А в точке а, необходимо и
имела предел равный А в точке а, необходимо и
Достаточно, чтобы существовали односторонние пределы функции в этой точке и
были равны между собой.
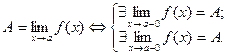
Теорема 1: Если существуют конечные пределы функций 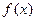 и
и 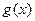 при
при 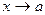 , то существует
, то существует
предел их суммы (разности), равный сумме (разности) пределов функций 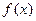 и
и 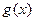 :
:
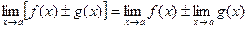
Теорема 2: Если существуют конечные пределы функций 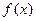 и
и 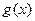 при
при 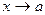 , то существует
, то существует
предел их произведения, равный произведению пределов функций 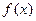 и
и 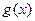 :
:
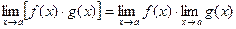
Теорема 3: Если существуют конечные пределы функций 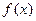 и
и 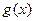 при
при 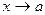 , то существует
, то существует
предел отношения 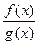 , равный отношению пределов функций
, равный отношению пределов функций 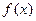 и
и 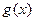 :
:
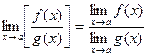 , где
, где 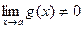
Следствия:
1. Постоянный множитель можно вынести за знак предела: 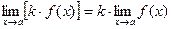 ,
, 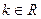 .
.
2. Если 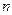 - натуральное число, то
- натуральное число, то 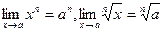 , при
, при 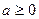 .
.
3. Предел многочлена 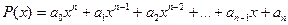 при
при 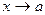 равен значению этого многочлена при
равен значению этого многочлена при 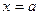 т.е.
т.е. 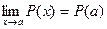 .
.
4. Предел дробно-рациональной функции 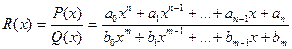 при
при 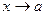 равен значению этой функции при
равен значению этой функции при 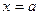 , если
, если 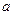 принадлежит области определения функции, т.е.
принадлежит области определения функции, т.е. 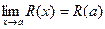 и
и 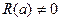 .
.
Важно знать некоторые пределы наизусть:
Первый замечательный предел- 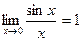
Следствия: 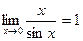
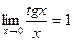
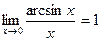
Второй замечательный предел - 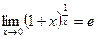
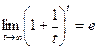
Следствия: 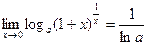
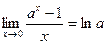
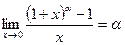
Функция 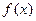 называется непрерывной в точке
называется непрерывной в точке 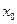 если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
Функция 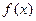 называется непрерывной в точке
называется непрерывной в точке 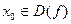 , если для любого
, если для любого 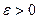 существует
существует 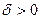 , такое, что для всех
, такое, что для всех 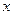 из области определения функции, удовлетворяющих условию
из области определения функции, удовлетворяющих условию 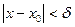 ,выполняется неравенство
,выполняется неравенство 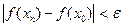 .
.
Функция 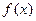 называется непрерывной в точке
называется непрерывной в точке 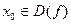 , если предел функции в этой точке существует и равен значению функции в этой точке.
, если предел функции в этой точке существует и равен значению функции в этой точке.
Условия непрерывности функции в точке:
1. 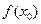 - определена.
- определена.
2. 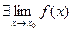
3. 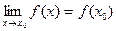
Теорема 1: Если функции 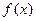 и
и 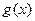 непрерывны в точке
непрерывны в точке 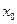 , то функция
, то функция 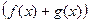 так же
так же
непрерывна в этой точке.
Теорема 2: Если функции 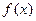 и
и 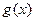 непрерывны в точке
непрерывны в точке 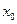 , то функция
, то функция 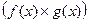 так же
так же
непрерывна в этой точке.
Теорема 3: Если функции 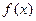 и
и 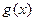 непрерывны в точке
непрерывны в точке 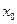 и
и 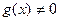 , то функция
, то функция
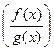 так же непрерывна в этой точке.
так же непрерывна в этой точке.
Свойства функций непрерывных на отрезке.
Теорема1: Больцано- Вейерштрасса об ограниченности непрерывной функции.
Если функция 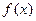 определена и непрерывна на отрезке
определена и непрерывна на отрезке 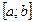 , то она ограничена на этом отрезке.
, то она ограничена на этом отрезке.
Теорема2: Больцано- Вейерштрасса о достижении верхней и нижней граней
Если функция 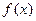 определена и непрерывна на отрезке
определена и непрерывна на отрезке 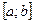 . Тогда эта функция принимает на отрезке
. Тогда эта функция принимает на отрезке 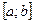 свои наибольшие и наименьшие значения, т.е. существуют такие точки
свои наибольшие и наименьшие значения, т.е. существуют такие точки 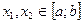 , что для любой точки
, что для любой точки 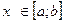 справедливы равенства
справедливы равенства 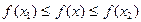 .
.
Теорема3: Больцано- Коши о нулях непрерывной функции
Если функция 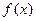 определена и непрерывна на отрезке
определена и непрерывна на отрезке 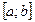 и на концах его принимает значения противоположных знаков, то существует точка
и на концах его принимает значения противоположных знаков, то существует точка  на этом отрезке в которой значение функции равно нулю
на этом отрезке в которой значение функции равно нулю 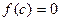 .
.
Теорема4: Больцано- Коши о промежуточных значениях непрерывной функции
Если функция 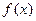 определена и непрерывна на отрезке
определена и непрерывна на отрезке 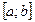 . Тогда для любого числа С, заключенного между числами
. Тогда для любого числа С, заключенного между числами 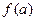 и
и 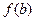 , найдется такая точка
, найдется такая точка 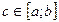 , что
, что 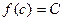
Если 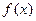 не является непрерывной в точке
не является непрерывной в точке 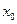 , то точка
, то точка 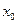 называется точкой разрыва функции.
называется точкой разрыва функции.
Условие непрерывности можно переписать следующим образом: 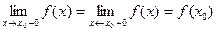 (*)
(*)
Если хотя бы одно из выражений в равенстве (*) не существует или не выполняется хотя бы одно из равенств, то точка 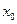 называется точкой разрыва функции.
называется точкой разрыва функции.
Точка 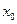 называется точкой разрыва устранимого режима, если односторонние пределы функции в этой точке существуют и равны между собой, но не равны значению функции в этой точке или функция в этой точке не определена.
называется точкой разрыва устранимого режима, если односторонние пределы функции в этой точке существуют и равны между собой, но не равны значению функции в этой точке или функция в этой точке не определена.
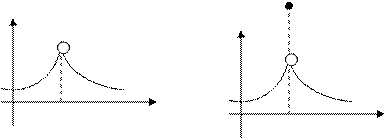
У у
0 х0 х 0 х0 х
Точка  называется точкой разрыва первого рода (скачок), если односторонние пределы функции в этой точке существуют но не равны между собой.
называется точкой разрыва первого рода (скачок), если односторонние пределы функции в этой точке существуют но не равны между собой.
у 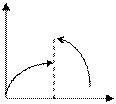
0 х0 х
 Точка
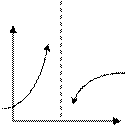
Точка  называется точкой разрыва второго рода, если хотя бы один из односторонних пределов функции в этой точке не существует или равен бесконечности.
называется точкой разрыва второго рода, если хотя бы один из односторонних пределов функции в этой точке не существует или равен бесконечности.
у
0 х0 х
Теорема: Если 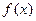 строго монотонна на
строго монотонна на 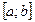 и
и 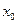 произвольная точка этого отрезка, то
произвольная точка этого отрезка, то
верхняя грань совпадает с левым пределом этой функции, не превосходит 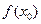 , не
, не
превосходит правого предела и не превосходит правой грани.
Утверждение1: Всякая строго монотонная на промежутке функция имеет односторонние пределы в
каждой точке этого промежутка.
Утверждение2: Если односторонние пределы строго монотонной функции в точке совпадают, то
функция непрерывна в этой точке.
Утверждение3: Если односторонние пределы строго монотонной функции в точке не совпадают, то
это точка разрыва первого рода (скачок).
Дата: 2019-02-02, просмотров: 364.