Тема 1.1. Лекция 1. Занятие 1.
Тема: Матрицы. Линейные операции над матрицами.
Матрицей называется прямоугольная таблица, составленная из чисел или каких-либо других объектов. У матрицы различают элементы, строки и столбцы. В общем виде:
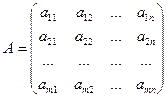
Первый индекс указывает номер строки, а второй номер столбца. Иногда коротко пишут: 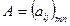 т.е. I меняется от 1 до m, а j от 1 до n.
т.е. I меняется от 1 до m, а j от 1 до n.
Пара чисел 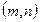 называется размерностью матрицы .
называется размерностью матрицы .
Если число строк равно числу столбцов, то матрица называется квадратной, тогда говорят о ее порядке.
Матрица, у которой всего один столбец называется столбцевой, или числовым вектором.
Матрица, у которой всего одна строка называется строчной.
Матрица, у которой все элементы равны нулю, называется нулевой. И обозначается 0.
Квадратная матрица, у которой равны нулю все элементы, кроме, быть может, стоящих на главной диагонали, называется диагональной.
Диагональная матрица, у которой все диагональные элементы равны единице, называется единичной
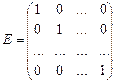
Иногда применяется транспонирование матрицы А, т.е. перемена ролями ее строк и столбцов, полученную матрицу обозначим 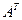 .
.
Действия над матрицами.
1. Матрицы одинакового размера можно складывать по формуле:
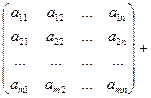
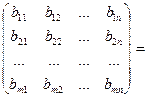
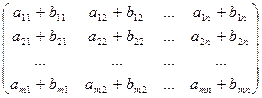 (1)
(1)
2. Матрицы можно умножать на число по формуле:
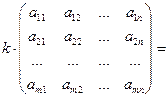
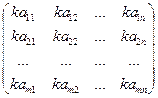 (2)
(2)
3. Если число столбцов в первой матрице равно числу строк во второй, то матрицы можно перемножать друг на друга по правилу:
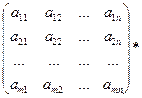
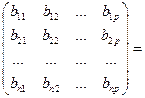
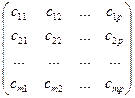 (3)
(3)
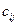 - получается путем умножения элементов I-той строки первой матрицы на элементы j-того столбца второй и результаты складываются.
- получается путем умножения элементов I-той строки первой матрицы на элементы j-того столбца второй и результаты складываются. 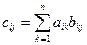
Схема умножения матриц: r

n
n
m
Квадратная матрица имеет определитель, который будем обозначать detА или 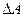 .
.
Тема 1.1 Лекция 2. Занятие 2
Обратная матрица.
Обратной к матрице А называется матрица 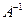 , такая, что
, такая, что 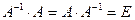 .
.
Квадратная матрица, для которой 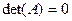 , называется вырожденной. Вырожденная матрица не имеет обратной, а всякая невырожденная матрица имеет обратную.
, называется вырожденной. Вырожденная матрица не имеет обратной, а всякая невырожденная матрица имеет обратную.
Возьмем невырожденную матрицу 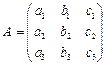 , тогда обратная будет
, тогда обратная будет 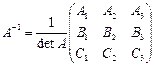 (7),
(7),
где большими буквами А1……С3 – обозначены алгебраические дополнения соответствующих элементов в матрице А.
Ранг матрицы.
Вычеркнем из матрицы А несколько строк и столбцов так, чтобы количество оставшихся строк равнялось количеству оставшихся столбцов. Если после этого заменить знак матрицы на знак определителя, то полученный определитель называется минором матрицы А Матрица имеет много миноров, причем некоторые из них могут равняться нулю, а другие отличны от нуля. Наивысший из порядков миноров, отличных от нуля, называется рангом матрицы А.
Ранг нулевой матрицы, у которой все миноры равны нулю, принимается равным нулю.
Ранг матрицы равен максимально возможному числу ее линейно независимых строк. Матрицу А с помощью элементарных преобразований сводят к ступенчатому виду и посчитают количество строк. Это и будет ранг матрицы.
Элементарные преобразования:
1. меняем местами строки.
2. прибавляем к одной строке другую, умноженную на какое либо число.
3. Отбрасываем нулевые строки.
Тема: Векторы на плоскости и в пространстве. Основные понятия.
Векторы на плоскости
Если началом вектора 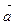 является точка А(
является точка А( 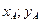 ), а концом В(
), а концом В( 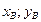 ) , то
) , то 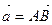 имеет координаты:
имеет координаты: 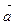 =
= 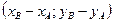 (1)
(1)
Над векторами, заданными своими координатами можно производить следующие действия: если 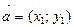 и
и 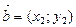 , то
, то 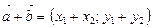 (2)
(2)
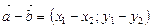 (3)
(3)
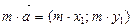 , где
, где 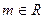 (4)
(4)
Вектор 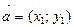 коллинеарен вектору
коллинеарен вектору 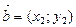 , если их координаты пропорциональны:
, если их координаты пропорциональны: 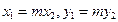 .
.
Расстояние между точками 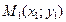 и
и 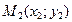 равно
равно 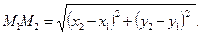 (5)
(5)
Следовательно длина вектора 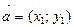 вычисляется по формуле
вычисляется по формуле 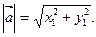 (6)
(6)
Если отрезок АВ разделен точкой С в отношении АС:СВ=λ. То координаты точки С находятся по формулам: 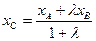 ;
; 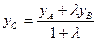 ; (7)
; (7)
Если λ=1, то получим формулы для середины отрезка: 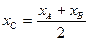 ;
; 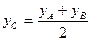 (8)
(8)
Скалярное произведение векторов, заданными своими координатами в пространстве вычисляется по формуле 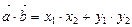 (10)
(10)
Косинус угла между векторами находится по формуле: 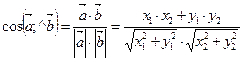 (11)
(11)
Условие перпендикулярности двух векторов: 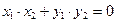
Векторы в пространстве
Если началом вектора 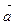 является точка А(
является точка А( 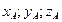 ), а концом В(
), а концом В( 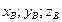 ) , то
) , то 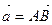 имеет координаты:
имеет координаты: 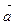 =
= 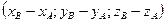 (12)
(12)
Над векторами, заданными своими координатами можно производить следующие действия: если 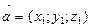 и
и 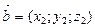 , то
, то 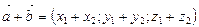 (13)
(13)
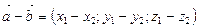 (14)
(14)
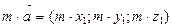 , где
, где  (15)
(15)
Вектор 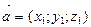 коллинеарен вектору
коллинеарен вектору 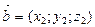 , если их координаты пропорциональны:
, если их координаты пропорциональны: 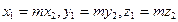 .
.
Расстояние между точками 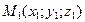 и
и 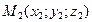 равно
равно 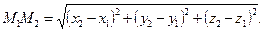 (16)
(16)
Следовательно длина вектора 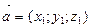 вычисляется по формуле
вычисляется по формуле 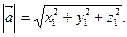 (17)
(17)
Если отрезок АВ разделен точкой С в отношении АС:СВ=λ. То координаты точки С находятся по формулам: 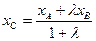 ;
; 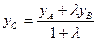 ;
; 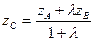 (18)
(18)
Если λ=1, то получим формулы для середины отрезка: 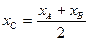 ;
; 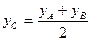 ;
;  (19) Направляющие косинусы вектора – это косинусы углов, которые он образует с осями координат.
(19) Направляющие косинусы вектора – это косинусы углов, которые он образует с осями координат.
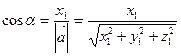 ;
; 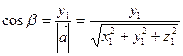 ;
;  (20)
(20)
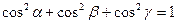 (21)
(21)
Скалярное произведение векторов, заданными своими координатами в пространстве вычисляется по формуле 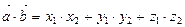 (22)
(22)
Косинус угла между векторами находится по формуле: 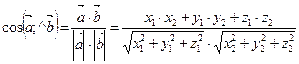 (23)
(23)
Условие перпендикулярности двух векторов: 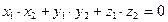
Прямая на плоскости.
Способы задания прямой основаны на аксиомах и теоремах школьного курса. Из школьного же курса известно общее уравнение прямой: 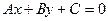 .
.
- Задание прямой проходящей через точку и имеющую данный угловой коэффициент.
Угловым коэффициентом прямой называется число, равное отношению второй координаты ее направляющего вектора к первой координате 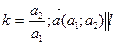
Замечание: Геометрический смысл углового коэффициента имеет смысл только в
ортонормированном базисе: 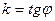 ,
, 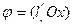
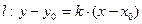
- Задание прямой проходящей через точку и имеющую данный нормальный вектор.
Всякий вектор, перпендикулярный прямой, называется нормальным вектором прямой.
Если прямая задана общим уравнением , то за нормальный вектор можно принять 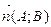 .
.
Дано: 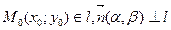 : .
: . 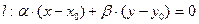
- Задание прямой через точку, принадлежащую этой прямой, и направляющий вектор.
Направляющим вектором 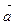 прямой
прямой 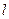 называется всякий вектор, параллельный этой прямой или лежащий на ней. Если прямая задана общим уравнением , то направляющим вектором является
называется всякий вектор, параллельный этой прямой или лежащий на ней. Если прямая задана общим уравнением , то направляющим вектором является 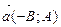 или
или 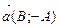 .
.
Дано: 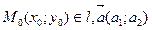 ||
|| 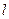 каноническое уравнение прямой будет:
каноническое уравнение прямой будет:
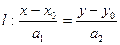 - . (13)
- . (13) 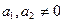
4. Задание прямой проходящей через две различные точки.
Дано: 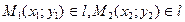 .
. 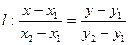
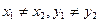
Условие перпендикулярности прямых: 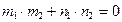
Угол между пересекающимися прямыми вычисляется по формуле: 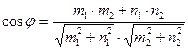
Условие параллельности прямых: 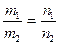
Понятие функции
Одним из основных математических понятий является понятие функции. Понятие функции связано с установлением зависимости (связи) между элементами двух множеств.
Пусть даны два непустых множества X и Y. Соответствие ƒ, которое каждому элементу хÎ X сопоставляет один и только один элемент уÎ Y, называется функцией и записывается у=ƒ(х), хÎ X или ƒ: X→Y. Говорят еще, что функция ƒ отображает множество X на множество Y.
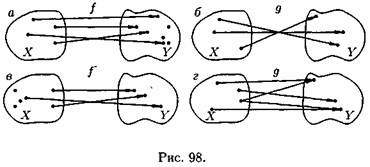
Например, соответствия ƒ и g, изображенные на рисунке 98 а и б, являются функциями, а на рисунке 98 в и г — нет. В случае в — не каждому элементу хÎX соответствует элемент уÎY. В случае г не соблюдается условие однозначности.
Множество X называется областью определения функции ƒ и обозначается D(f). Множество всех уÎY называется множеством значений функции ƒ и обозначается Е(ƒ).
Числовые функции. График функции. Способы задания функций
Пусть задана функция ƒ : X→Y.
Если элементами множеств X и Y являются действительные числа (т. е. XÌ R и YÌ R), то функцию ƒ называют числовой функцией. В дальнейшем будем изучать (как правило) числовые функции, для краткости будем именовать их просто функциями и записывать у=ƒ(х).
Переменная х называется при этом аргументом или независимой переменной, а у — функцией или зависимой переменной (от х). Относительно самих величин х и у говорят, что они находятся в функциональной зависимости. Иногда функциональную зависимость у от х пишут в виде у=у(х), не вводя новой буквы (ƒ) для обозначения зависимости.
Частное значение функции ƒ(х) при х=a записывают так: ƒ(a). Например, если ƒ(х)=2х2-3, то ƒ(0)=-3, ƒ(2)=5.
Графиком функции у=(х) называется множество всех точек плоскости Оху, для каждой на которых х является значением аргумента, а у — соответствующим значением функции.
Например, графиком функции у=√(1-х2) является верхняя полуокружность радиуса R=1 с центром в О(0;0) (см. рис. 99).
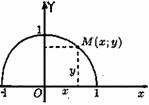
Чтобы задать функцию у=ƒ(х), необходимо указать правило, позволяющее, зная х, находить соответствующее значение у.
Наиболее часто встречаются три способа задания функции: аналитический, табличный, графический.
Аналитический способ: функция задается в виде одной или нескольких формул или уравнений.
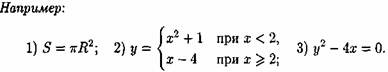
Если область определения функции у = ƒ(х) не указана, то предполагается, что она совпадает с множеством всех значений аргумента, при которых соответствующая формула имеет смысл. Так, областью определения функции у= √(1-х2)является отрезок [-1; 1].
Аналитический способ задания функции является наиболее совершенным, так как к нему приложены методы математического анализа, позволяющие полностью исследовать функцию у=ƒ(х).
Графический способ: задается график функции.
Часто графики вычерчиваются автоматически самопишущими приборами или изображаются на экране дисплея. Значения функции у, соответствующие тем или иным значениям аргумента х, непосредственно находятся из этого графика.
Преимуществом графического задания является его наглядность, недостатком — его неточность.
Табличный способ: функция задается таблицей ряда значений аргумента и соответствующих значений функции. Например, известные таблицы значений тригонометрических функций, логарифмические таблицы.
На практике часто приходится пользоваться таблицами значений функций, полученных опытным путем или в результате наблюдений.
Основные характеристики функции
1. Функция у=ƒ(х), определенная на множестве D, называется четной, если " xÎ D выполняются условия -хєD и ƒ(-х)=ƒ(х);нечетной, если " xєD выполняются условия -хєD и ƒ(-х)=-ƒ(х).
График четной функции симметричен относительно оси Оу, а нечетной — относительно начала координат.
Например, у=х2, у=√(1+х2), у=ln|х| — четные функции; а у=sinx, у=х3 — нечетные функции; у=х-1, у=√x — функции общего вида, т. е. не четные и не нечетные.
2. Пусть функция у=ƒ(х) определена на множестве D и пусть D1єD. Если для любых значений х 1;x2єD1 аргументов из неравенства x1<x2 вытекает неравенство: ƒ(x 1)<ƒ(х2), то функция называется возрастающей на множестве D 1; f(x1) ≤ ƒ(х2), то функция называется неубывающей на множестве D1; f(x1)>ƒ(х2), то функция называется убывающей на множестве D1; ƒ(х1)≥ƒ(x2), то функция называется невозрастающей на множестве D1.
Например, функция, заданная графиком (см. рис. 100), убывает на интервале (-2; 1), не убывает на интервале (1; 5), возрастает на интервале (3; 5).
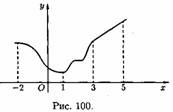
Возрастающие, невозрастающие, убывающие и неубывающие функции на множестве D1 называются монотонными на этом множестве, а возрастающие и убывающие — строго монотонными. Интервалы, в которых функция монотонна, называются интервалами монотонности. На рисунке (выше) функция строго монотонна на (-2; 1) и (3; 5); монотонна на (1;3).
3. Функцию у=ƒ(х), определенную на множестве D, называют ограниченной на этом множестве, если существует такое число М>0, что для всех хєD выполняется неравенство |ƒ(х)|≤М (короткая запись: у=ƒ(х), хєD, называется ограниченной на D, если $М>0: """xєD ==>|ƒ(х)|≤М). Отсюда следует, что график ограниченной функции лежит между прямыми у=-М и у=М (см. рис. 101).
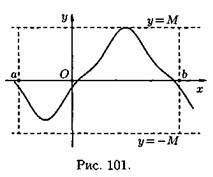
4. Функция у=ƒ(х), определенная на множестве D, называется периодической на этом множестве, если существует такое число Т>0, что при каждом хєD значение (х+Т)єD и ƒ(х+Т)=ƒ(х). При этом число Т называется периодом функции. Если Т— период функции, то ее периодами будут также числа m•Т, где m=±1;±2,... Так, для у=sinx периодами будут числа ±2π;±4π; ±6π,... Основной период (наименьший положительный) — это период Т=2π. Вообще обычно за основной период берут наименьшее положительное число Т, удовлетворяющее равенству ƒ(х+Т)=ƒ(х).
Обратная функция
Пусть задана функция у=ƒ(х) с областью определения D и множеством значений Е. Если каждому значению уєЕ соответствует единственное значение хєD, то определена функция х=φ(у) с областью определения Е и множеством значений D (см. рис. 102).
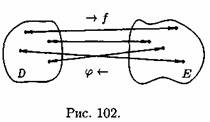
Такая функция φ(у) называется обратной к функции ƒ(х) и записывается в следующем виде: х=j(y)=f-1(y).Про функции у=ƒ(х) и х=φ(у) говорят, что они являются взаимно обратными. Чтобы найти функцию х=φ(у), обратную к функции у=ƒ (х), достаточно решить уравнение ƒ(х)=у относительно х (если это возможно).
Примеры:
1. Для функции у=2х обратной функцией является функция х=у/2;
2.Для функции у=х2 хє[0;1] обратной функцией является х=√у;заметим, что для функции у=х2, заданной на отрезке [-1; 1], обратной не существует, т. к. одному значению у соответствует два значения х (так, если у=1/4, то х1=1/2, х2=-1/2).
Из определения обратной функции вытекает, что функция у=ƒ(х) имеет обратную тогда и только тогда, когда функция ƒ(х) задает взаимно однозначное соответствие между множествами D и Е. Отсюда следует, что любая строго монотонная функция имеет обратную. При этом если функция возрастает (убывает), то обратная функция также возрастает (убывает).
Заметим, что функция у=ƒ(х) и обратная ей х=φ(у) изображаются одной и той же кривой, т. е. графики их совпадают. Если же условиться, что, как обычно, независимую переменную (т. е. аргумент) обозначить через х, а зависимую переменную через у, то функция обратная функции у=ƒ(х) запишется в виде у=φ(х).
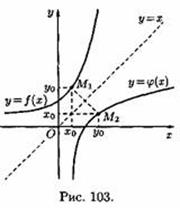
Это означает, что точка M1(xo;yo) кривой у=ƒ(х) становится точкой М2(уо;хо) кривой у=φ(х). Но точки M1 и М2 симметричны относительно прямой у=х (см. рис. 103). Поэтому графики взаимно обратных функции у=ƒ(х) и у=φ(х) симметричны относительно биссектрисы первого и третьего координатных углов.
Сложная функция
Пусть функция у=ƒ(u) определена на множестве D, а функция u= φ(х) на множестве D1, причем для " xÎ D1 соответствующее значение u=φ(х) є D. Тогда на множестве D 1 определена функция u=ƒ(φ(х)), которая называется сложной функцией от х (или суперпозицией заданных функций, или функцией от функции).
Переменную u=φ(х) называют промежуточным аргументом сложной функции.
Например, функция у=sin2x есть суперпозиция двух функций у=sinu и u=2х. Сложная функция может иметь несколько промежуточных аргументов.
Основные элементарные функции и их графики
Основными элементарными функциями называют следующие функции.
1) Показательная функция у=aх,a>0, а ≠ 1. На рис. 104 показаны графики показательных функций, соответствующие различным основаниям степени.
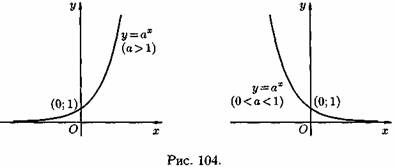
2) Степенная функция у=хα, αєR. Примеры графиков степенных функций, соответствующих различным показателям степени, предоставлены на рисунках
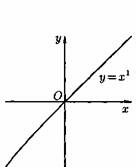
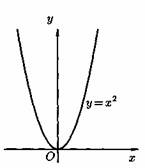
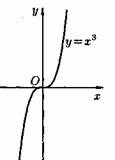
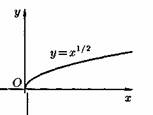
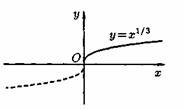
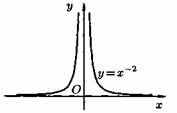
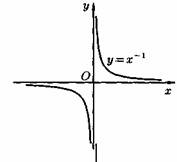
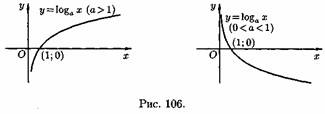
3)Логарифмическая функция y=logax, a>0,a≠1;Графики логарифмических функций, соответствующие различным основаниям, показаны на рис. 106.
4) Тригонометрические функции у=sinx, у=cosx, у=tgх, у=ctgx; Графики тригонометрических функций имеют вид, показанный на рис. 107.
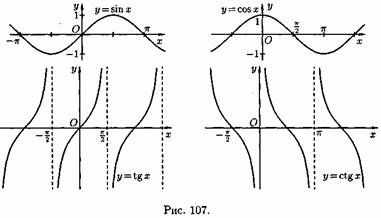
5) Обратные тригонометрические функции у=arcsinx, у=arccosх, у=arctgx, у=arcctgx. На рис. 108 показаны графики обратных тригонометрических функций.
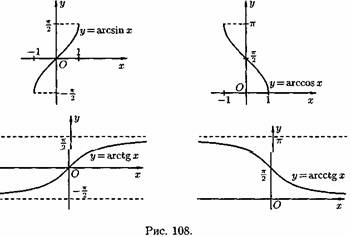
Функция, задаваемая одной формулой, составленной из основных элементарных функций и постоянных с помощью конечного числа арифметических операций (сложения, вычитания, умножения, деления) и операций взятия функции от функции, называется элементарной функцией.
Примерами элементарных функций могут служить функции
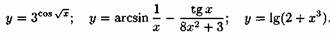
Примерами неэлементарных функций могут служить функции
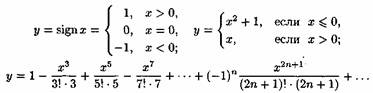
Интегрирование по частям
Теорема: Пусть даны две функции 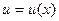 и
и 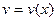 , дифференцируемы на промежутке
, дифференцируемы на промежутке 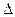 . Если существует интеграл
. Если существует интеграл 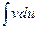 , следовательно, существует интеграл
, следовательно, существует интеграл 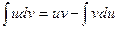 .
.
Условно интегралы, берущиеся по частям, можно разбить на группы.
1. 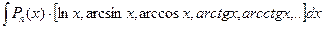
за 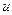 обозначают то что в скобках, а за
обозначают то что в скобках, а за 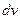 все остальное.
все остальное.
2. 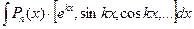
за 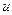 обозначают
обозначают 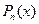 , а за
, а за 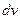 все остальное.
все остальное.
3. 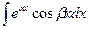
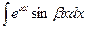 берутся с помощью повторного интегрирования (за u берем
берутся с помощью повторного интегрирования (за u берем 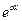 ,
,
за 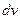 все остальное)
все остальное)
Задача вычисления пути.
Материальная точка движется прямолинейно с некоторой мгновенной скоростью 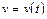 . Требуется найти путь, который пройдет тело за промежуток времени от
. Требуется найти путь, который пройдет тело за промежуток времени от 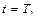 до
до 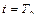
Если 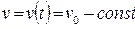 , то
, то 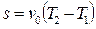 .
.
Если 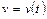 - функция, то путь
- функция, то путь 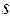 , пройденный телом, определяется из равенства
, пройденный телом, определяется из равенства
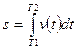 при
при 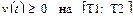 и
и 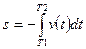 при
при 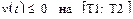
Тема 1.1. Лекция 1. Занятие 1.
Дата: 2019-02-02, просмотров: 478.