Выражение 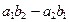 называется определителем ( детерминантом) второго порядка и записывается в виде:  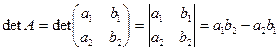       ,                      (4)

где вертикальные черточки – знак определителя.

Аналогично определитель матрицы третьего порядка: 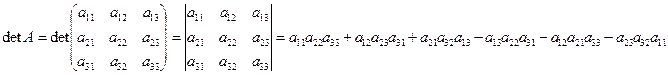  (5)

Это выражение называется определителем третьего порядка .

Данный определитель можно вычислить по правилу треугольника:

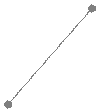
Главная диагональ и треугольники с основаниями,                                                                                        параллельными главной диагонали со знаком плюс.

побочная диагональ и треугольники с основаниями,                                                                                        параллельными побочной диагонали со знаком минус.

Определитель третьего порядка имеет три строки (горизонтальные ряды), три столбца

 (вертикальные ряды), девять элементов ( числа .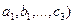

Свойства определителей:

1. Если переставить два параллельных ряда , т.е. две строки или два столбца, то определитель умножится на –1.

2. Если определитель имеет два одинаковых ряда, то он равен нулю.

3. Общий множитель, содержащийся во всех элементах одного ряда, можно вынести за знак определителя.

4. Определитель, имеющий нулевой ряд, равен нулю.

5. Если к каждому из элементов какого-либо ряда прибавить числа, пропорциональные соответствующим элементам какого-нибудь другого ряда, параллельному первому, то значение определителя не изменится.

6. Определитель не меняется, если заменить его строки столбцами и обратно. Это называется транспонированием определителя.

 Разложение определителя по элементам ряда:

Алгебраическим дополнением к элементу называется определитель, полученный из данного вычеркиванием строки и столбца, в которых находится данный элемент. Но этот определитель надо взять со знаком «+» или «-« , в зависимости от положения данного элемента в исходном определителе: если сумма индексов элемента четна, то берется со знаком «+», если нечетно, то «-«. Обозначается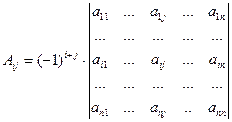

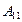В определителе (5 ) алгебраическое дополнение элемента  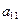равно ,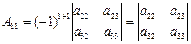

алгебраическое дополнение 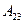 элемента  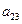равно  и т.д.

       Имеет место следующее свойство определителей: определитель равен сумме произведений элементов какого-нибудь из рядов на алгебраические дополнения этих элементов.

Например: Разложение определителя по элементам первой строки:

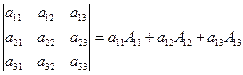(6)

Обратная матрица.

Обратной к матрице А называется матрица 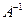, такая, что .

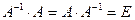       Квадратная матрица, для которой 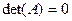, называется вырожденной. Вырожденная матрица не имеет обратной, а всякая невырожденная матрица имеет обратную.

Возьмем невырожденную матрицу 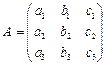, тогда обратная будет  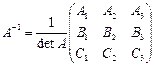(7),

 где большими буквами А₁……С₃ – обозначены алгебраические дополнения соответствующих элементов в матрице А.

Ранг матрицы.

       Вычеркнем из матрицы А несколько строк и столбцов так, чтобы количество оставшихся строк равнялось количеству оставшихся столбцов. Если после этого заменить знак матрицы на знак определителя, то полученный определитель называется минором матрицы А Матрица имеет много миноров, причем некоторые из них могут равняться нулю, а другие отличны от нуля. Наивысший из порядков миноров, отличных от нуля, называется рангом матрицы А.

       Ранг нулевой матрицы, у которой все миноры равны нулю, принимается равным нулю.

       Ранг матрицы равен максимально возможному числу ее линейно независимых строк. Матрицу А с помощью элементарных преобразований сводят к ступенчатому виду и посчитают количество строк. Это и будет ранг матрицы.

       Элементарные преобразования:

1. меняем местами строки.

2. прибавляем к одной строке другую, умноженную на какое либо число.

3. Отбрасываем нулевые строки.