Окружностью называется совокупность всех точек плоскости, равноудаленных от одной данной точки, называемой центром окружности. Расстояние от центра окружности до любой точки на окружности называется. радиусом окружности.

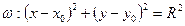- каноническое уравнение окружности (16) 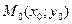- центр окружности.

Если центр окружности лежит в начале координат, то уравнение окружности 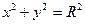           (16^.)

Эллипсом называется совокупность всех точек плоскости, сумма расстояний которых от двух данных точек этой плоскости ( называемых фокусами этого эллипса) есть величина постоянная.

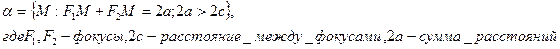
                                                                        Y                                                

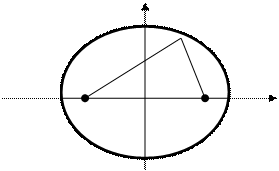                                                                        В (0;b)M(x,y)

                                                                     r₁           r₂       r₁+r₂=2a

                                        А                   O                С

                                                 (-а;0) F₁(-c;0) 0 F₂(c;0) (а;0)      X                                                                     

                                                                        D (0;-b)

 Обозначим для краткости a²-b²=c²(*), тогда уравнение эллипса: 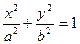                (17)

Если положить y=0, то получается 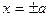 , а если положить х=0, получается 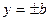; значит,  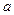 и 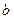 - это длины полуосей эллипса – большой ( 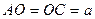) и малой ( 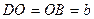). Кроме того, каждое из слагаемых в левой части не может быть больше единицы, откуда 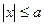, , 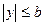и потому весь эллипс расположен внутри прямоугольника. Точки A,B,C,D, в которых эллипс пересекается своими осями симметрии, называются вершинами эллипса.

Отношение 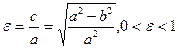 называется эксцентриситетом эллипса.

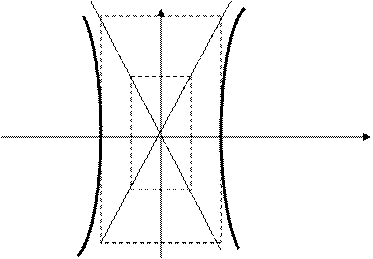
Гиперболой называется совокупность всех точек плоскости, модуль разности расстояний которых от двух данных точек этой плоскости ( называемых фокусами этой гиперболы) есть величина постоянная. Середина расстояния между фокусами называется центром гиперболы.

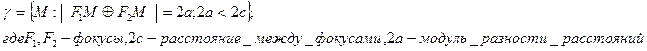
                                                                                                  M(x;y)                                                                                                                                                                                                                                                                                                         

                                                                                  r₁           

                                                                                                     r₂ r₁ –r₂=2a                                                                                                                                        

                                                 F₁(-c;0)               0           F₂(c;0)                          x      

Обозначим a²-c²=-b² (**),уравнение гиперболы: 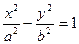                    (18)

Из этого уравнения видно, что и гипербола имеет две оси симметрии ( главные оси), а так же центр симметрии ( центр гиперболы).

Отношение 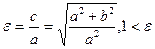 называется эксцентриситетом гиперболы.

Если положить y=0, то получается 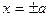 , а если положить х=0, получается .

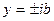Значит ось Ох пересекает гиперболу в двух точках ( вершинах гиперболы), это – вещественная ось; Ось Оу гиперболу не пересекает – это «мнимая ось.» Всякий отрезок, соединяющий две точки гиперболы, если он проходит через центр, называется диаметром гиперболы.

Прямая, к которой кривая линия приближается сколь угодно близко, но никогда не пересекает ее называется асимптотой кривой. Гипербола имеет две асимптоты. Их уравнения: 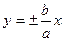          (19)

Параболой называется совокупность всех точек плоскости расстояние от каждой из которых до данной точки (называемой фокусом) равно расстоянию до данной прямой ( называемой директрисой).

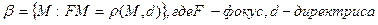
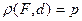- параметр параболы.

Парабола имеет одну ось симметрии. Точка пересечения параболы с осью симметрии называется вершиной параболы.

Каноническое уравнение параболы с вершиной в начале координат, осью симметрии которой служит ось Ох и ветви направлены вправо имеет вид 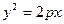                                                      (20)

Уравнение ее директрисы :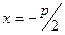

Каноническое уравнение параболы с вершиной в начале координат, осью симметрии которой служит ось Ох и ветви направлены влево имеет вид 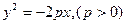                                              (20^,)

Уравнение ее директрисы :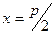

Каноническое уравнение параболы с вершиной в начале координат, осью симметрии которой служит ось Оу и ветви направлены вверх имеет вид 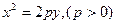                                             (20^,,)

Уравнение ее директрисы :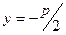

Каноническое уравнение параболы с вершиной в начале координат, осью симметрии которой служит ось Оу и ветви направлены вниз имеет вид 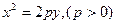                                                (20^,,,)

Уравнение ее директрисы :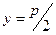

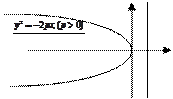
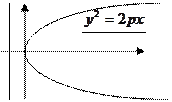                                                  y                                 y

                                          F      0 p/2 x        -p/2 0                      x

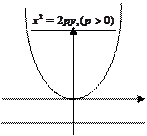                                 Y                                                            y

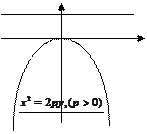                                                                                                      p/2

0 x

1    

0 x

                                        –p/2
Тема 2.1. Лекция 7.Занятие 10