Расширенной матрицей системы линейных уравнений называется таблица, составленная из коэффициентов при неизвестных и свободных членов, записанных в строку.
Теорема Кронекера-Капелли: Для того, чтобы матрица линейных уравнений была совместна необходимо и достаточно, чтобы ранг матрицы системы равнялся рангу расширенной матрицы системы.
Пусть дана система m линейных уравнений с n неизвестными. 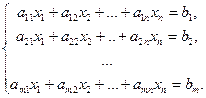
первое уравнение при 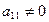 оставим без изменения ( если
оставим без изменения ( если 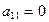 то поставим на первое место уравнение в котором первый коэффициент отличен от нуля), удобнее когда
то поставим на первое место уравнение в котором первый коэффициент отличен от нуля), удобнее когда 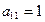 .
.
Умножим первое уравнение на 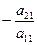 и прибавим ко второму. Получим
и прибавим ко второму. Получим 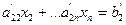
К третьему уравнению прибавим первое, умноженное на 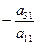 получим
получим 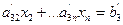
Эту операцию проделаем со всеми уравнениями, и последнее уравнение будет 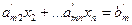
Если 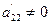 то с помощью второго уравнения исключаем
то с помощью второго уравнения исключаем  в 3,4,…,m уравнениях, умножая его на
в 3,4,…,m уравнениях, умножая его на 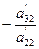 и складывая с третьим уравнением. Аналогично со всеми остальными уравнениями.
и складывая с третьим уравнением. Аналогично со всеми остальными уравнениями.
Повторяя эту операцию, получим систему линейных уравнений:
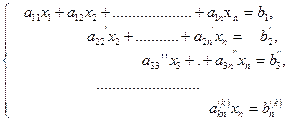 (5)
(5)
Процесс этот конечен.
Возможны три случая:
- Когда на каком то шаге получим уравнение вида
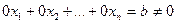 , значит, система не совместна, т.е. не имеет решения.
, значит, система не совместна, т.е. не имеет решения. - В ходе преобразований система сводится к треугольному виду: в первом n неизвестных, во втором n-1, в последнем 1. В этом случае система имеет единственное решение. Из последнего уравнения находим
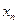 и последовательно все остальные.
и последовательно все остальные. - Система может свестись к трапециидальному виду. В последнем уравнении больше чем 1 неизвестное. Тогда система имеет множество решений. Тогда неизвестные
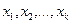 , которые образуют треугольник будут основными, а
, которые образуют треугольник будут основными, а 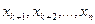 - свободные. Члены, содержащие свободные неизвестные переносятся в правую часть, т.е. основные неизвестные выражаются через свободные. Таким образом, получим общее решение системы. Придав свободным неизвестным произвольные числовые значения и найдя основные получим частное решение.
- свободные. Члены, содержащие свободные неизвестные переносятся в правую часть, т.е. основные неизвестные выражаются через свободные. Таким образом, получим общее решение системы. Придав свободным неизвестным произвольные числовые значения и найдя основные получим частное решение.
Решение систем линейных уравнений с помощью обратной матрицы.
Систему линейных уравнений можно представить в виде матричного уравнения вида AX=B и, где А и В известные матрицы а X неизвестная.
Рассмотрим несколько случаев.
- А- квадратная матрица и det А=0, В- квадратная матрица и ее detВ
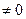 то уравнение решений не имеет.
то уравнение решений не имеет. - А- квадратная матрица и det А
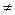 0 в этом случае существует
0 в этом случае существует 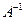 , такая, что
, такая, что 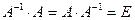 , поэтому умножая первое уравнение на
, поэтому умножая первое уравнение на 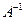 слева получим:
слева получим: 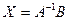
Тема 1.3. Лекция 5. Занятие 7.
Тема: Векторы на плоскости и в пространстве. Основные понятия.
Векторы на плоскости
Если началом вектора 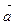 является точка А(
является точка А( 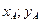 ), а концом В(
), а концом В( 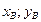 ) , то
) , то 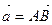 имеет координаты:
имеет координаты: 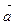 =
= 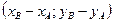 (1)
(1)
Над векторами, заданными своими координатами можно производить следующие действия: если 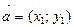 и
и 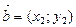 , то
, то 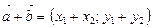 (2)
(2)
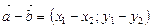 (3)
(3)
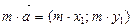 , где
, где 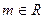 (4)
(4)
Вектор 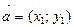 коллинеарен вектору
коллинеарен вектору 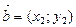 , если их координаты пропорциональны:
, если их координаты пропорциональны: 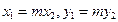 .
.
Расстояние между точками 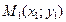 и
и 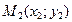 равно
равно 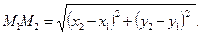 (5)
(5)
Следовательно длина вектора 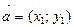 вычисляется по формуле
вычисляется по формуле 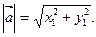 (6)
(6)
Если отрезок АВ разделен точкой С в отношении АС:СВ=λ. То координаты точки С находятся по формулам: 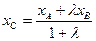 ;
; 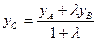 ; (7)
; (7)
Если λ=1, то получим формулы для середины отрезка: 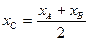 ;
; 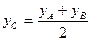 (8)
(8)
Скалярное произведение векторов, заданными своими координатами в пространстве вычисляется по формуле 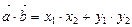 (10)
(10)
Косинус угла между векторами находится по формуле: 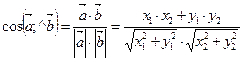 (11)
(11)
Условие перпендикулярности двух векторов: 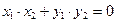
Векторы в пространстве
Если началом вектора 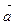 является точка А(
является точка А( 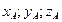 ), а концом В(
), а концом В( 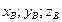 ) , то
) , то 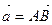 имеет координаты:
имеет координаты: 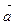 =
= 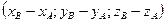 (12)
(12)
Над векторами, заданными своими координатами можно производить следующие действия: если 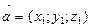 и
и 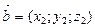 , то
, то 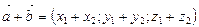 (13)
(13)
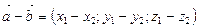 (14)
(14)
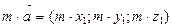 , где
, где  (15)
(15)
Вектор 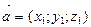 коллинеарен вектору
коллинеарен вектору 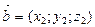 , если их координаты пропорциональны:
, если их координаты пропорциональны: 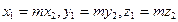 .
.
Расстояние между точками 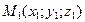 и
и 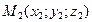 равно
равно 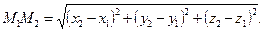 (16)
(16)
Следовательно длина вектора 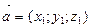 вычисляется по формуле
вычисляется по формуле 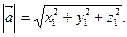 (17)
(17)
Если отрезок АВ разделен точкой С в отношении АС:СВ=λ. То координаты точки С находятся по формулам: 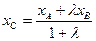 ;
; 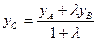 ;
; 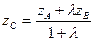 (18)
(18)
Если λ=1, то получим формулы для середины отрезка: 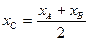 ;
; 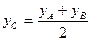 ;
;  (19) Направляющие косинусы вектора – это косинусы углов, которые он образует с осями координат.
(19) Направляющие косинусы вектора – это косинусы углов, которые он образует с осями координат.
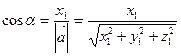 ;
; 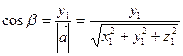 ;
;  (20)
(20)
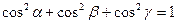 (21)
(21)
Скалярное произведение векторов, заданными своими координатами в пространстве вычисляется по формуле 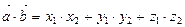 (22)
(22)
Косинус угла между векторами находится по формуле: 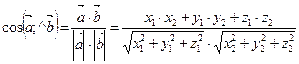 (23)
(23)
Условие перпендикулярности двух векторов: 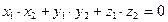
Прямая на плоскости.
Способы задания прямой основаны на аксиомах и теоремах школьного курса. Из школьного же курса известно общее уравнение прямой: 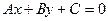 .
.
- Задание прямой проходящей через точку и имеющую данный угловой коэффициент.
Угловым коэффициентом прямой называется число, равное отношению второй координаты ее направляющего вектора к первой координате 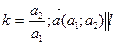
Замечание: Геометрический смысл углового коэффициента имеет смысл только в
ортонормированном базисе: 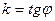 ,
, 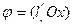
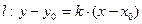
- Задание прямой проходящей через точку и имеющую данный нормальный вектор.
Всякий вектор, перпендикулярный прямой, называется нормальным вектором прямой.
Если прямая задана общим уравнением , то за нормальный вектор можно принять 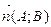 .
.
Дано: 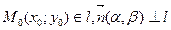 : .
: . 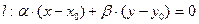
- Задание прямой через точку, принадлежащую этой прямой, и направляющий вектор.
Направляющим вектором 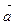 прямой
прямой 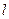 называется всякий вектор, параллельный этой прямой или лежащий на ней. Если прямая задана общим уравнением , то направляющим вектором является
называется всякий вектор, параллельный этой прямой или лежащий на ней. Если прямая задана общим уравнением , то направляющим вектором является 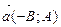 или
или 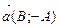 .
.
Дано: 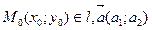 ||
|| 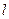 каноническое уравнение прямой будет:
каноническое уравнение прямой будет:
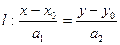 - . (13)
- . (13) 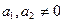
4. Задание прямой проходящей через две различные точки.
Дано: 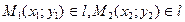 .
. 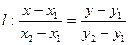
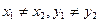
Условие перпендикулярности прямых: 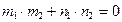
Угол между пересекающимися прямыми вычисляется по формуле: 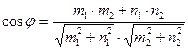
Условие параллельности прямых: 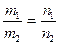
Дата: 2019-02-02, просмотров: 338.