| Теория | Вид перехода от одной инерциальной системы отсчета к другой | Свойства пространства и времени, выявляемые этим переходом | Принцип, удостоверяющий инвариантность законов данной теории относительно соответствующих преобразований |
| Классическая механика | Преобразования Галилея | Абсолютное пространство и абсолютное время | Принцип относительности Галилея |
| Специальная теория относительности | Преобразования Лоренца | Относительность пространства и времени, единое пространство-время | Принцип относительности Пуанкаре – Эйнштейна |
тность законов природы, или, что то же самое, их симметрия. С ним соглаша-лся В.И. Вернадский, отмечавший, что «новым в науке явилось не выявление принципа симметрии, а выявление его всеобщности». Негласный лозунг физиков-теоретиков – правильная теория должна быть красивой – также связан с симметрийными представлениями о последней. В свете сказанного мо-жно, пожалуй, утверждать, что знакомую нам последовательность реализации теоретического этапа научного метода (см. рис. 1.5) необходимо было бы дополнить еще одной процедурой – проверкой закона, как верифицированной гипотезы (там же) на симметричность.
Одним из подтверждений эффективности такого приема повышения ка-чества научного знания является проверка симметричности законов еще одной, более поздней естественнонаучной теории – квантовой механики – от-носительно преобразований другого пространства-времени, в котором движу-тся её объекты исследования – элементарные частицы. Это микропростран-ство существенно отличается от того макропространства, по отношению к которому осуществимы преобразования, указанные в таблице 2.2 – оно ква-нтованное, движущиеся в нем материальные объекты (системы уже не макро-скопических тел, а элементарных частиц) имеют ярко выраженную двойстве-нную (вещественно-полевую), а то и виртуальную природу, эти частицы могут взаимно превращаться друг в друга и т.д. В силу такой специфики симметрию законов квантовой механики пришлось доказывать другими внешними мысленными преобразованиями системы элементарных частиц, имеющими дискретный (табл. 2.5), а не непрерывный, как для макроскопических тел (левый столбец табл. 2.2), характер Дискретными они называются потому, что производятся в один прием, причем повторение этого приема возвращает преобразуемую материальную систему в первоначальное состояние.
Особенностью указанных в левом столбце таблицы 2.5 преобразований
Таблица 2.5
Дискретные преобразования систем элементарных частиц
и свойства пространства-времени, выявляемые этими преобразованиями
| Внешние мысленные преобразования систем элементарных частиц | Свойства (симметрии) пространства-време-ни, выявляемые этими преобразованиями |
| Зарядовое сопряжение (С) – замена всех частиц системы на античастицы | Массы и время жизни частиц и античастиц равны. Вероятности реализации в пространстве-времени процессов с частицами и античастицами одинаковы. |
| Пространственная инверсия (Р) – измене-ние пространственных координат частиц на противоположные по знаку | |
| Обращение времени (Т) – замена знака вре-мени в уравнениях, описывающих поведение системы частиц |
является и то, что производятся они одновременно, и потому имеют общее название СРТ-преобразования (читается «цэ–пэ–тэ», поскольку данная абб-ревиатура – латынь. В частности, буква С – это первая буква французского слова charge – заряд). И один из законов квантовой механики, называемый теоремой СРТ (физики Г. Людерс (Германия) и В. Паули (Швейцария), 1951 – 1955 гг.), гласит – уравнения квантовой механики инвариантны относительно СРТ-преобразования. С одной стороны, практическим подтверждением свойств пространства-времени, которые следуют из данной теоремы (правый столбец той же таблицы), является симметрично протекающая аннигиляция, обнаруженная еще в 1933 г. для пары «электрон – позитрон», а с другой – тот факт, что на опыте ни одного случая нарушения теоремы СРТ не обнаружено.
По аналогии с теоремой Нётер (но не вследствие применения её к сис-темам элементарных частиц!), из дискретных преобразований данных систем (левый столбец табл. 2.5) следуют иные, нежели выводимые из данной теоре-мы (см. табл. 2.3), законы сохранения для микрообъектов:
· закон сохранения электрического заряда системы элементарных частиц при их взаимодействиях и взаимопревращениях друг в друга. Данный закон, кстати, справедлив и для макросистем (М. Фарадей, 1843 г.);
· закон сохранения барионного заряда при сильных взаимодействиях тя-желых элементарных частиц – барионов;
· закон сохранения лептонного заряда при слабом взаимодействии легких элементарных частиц – лептонов и другие законы.
Как следует из сказанного, теорема СРТ удостоверила симметричность законов квантовой механики точно так же, как ранее это сделали принципы относительности Галилея и Пуанкаре – Эйнштейна по отношению к законам других естественнонаучных теорий – классической механики и специальной теории относительности соответственно (см. табл. 2.4). Общим для всех этих трех законов физики является то, что они доказали симметричность «своих» теорий только относительно пространственно-временных преобразований, как внешних по отношению к материальным системам (макроскопическим телам и системам элементарных частиц), поведение которых эти теории описывают. Разница, напомним, лишь в том, что для макрообъектов данные пре-образования осуществляются непрерывно, а для микрообъектов – дискретно.
Подведем некий промежуточный итог. К началу четвертого этапа истории естествознания (см. тему 1.3) симметрия, как научная категория доказала свою эффективность в двух аспектах. С одной стороны, она обнаружила связь с важнейшими законами физики – законами сохранения – и продемонс-трировала способ их выводить (доказывать математически). С другой стороны, она указала новый путь решения проблемы наглядности физических представлений – математического же доказательства существования новых, не поддающемуся иному подтверждению, свойств форм бытия материи (пространства и времени) проверкой законов физики на симметричность.
Еще более значимый результат использования представлений симметрии для продвижения по пути познания мира был получен на самом четвертом этапе развития науки. Чтобы эту значимость оценить в полной мере, нео-бходимо напомнить о такой неотъемлемой черте научного знания, как относительность его полноты и правоты (см. тему 1.2). Конкретно имеется в виду общая теория относительности, которая, как уже говорилось, была великим достижением в решении проблемы объяснения единой природы про-странства, времени и гравитации (см. тему 2.3). Тем не менее, она не смогла стать основой для создания в дальнейшем теории более высокого порядка сложности и достоверности, объясняющей такую же единую природу тоже бóльшего числа явлений и условий существования реальности – электромагнетизма, гравитации, пространства и времени (имеется в виду неудача Эйнштейна в создании единой теории поля, там же).
Решение данной задачи в начале 20-х годов прошлого века предложил уже упоминавшийся выше немецкий математик и физик Г. Вейль. В продолжение идей Эйнштейна он считал, что законы физики, описывающие природу разных фундаментальных взаимодействий, должны быть одними и теми же – это требование принципа относительности Пуанкаре – Эйнштейна (см. тему 2.2). Но для того, чтобы они одновременно учитывали природу известных к данному моменту времени действительно разных гравитационных и электромагнитных явлений, он предложил так же по-разному задавать (градуировать, калибровать) параметры единого пространства-вре-мени, как аргументы этих уравнений. С помощью знакомого нам интервала s (там же) это можно пояснить следующим образом. Согласно гипотезе Вейля, в любой точке пространства-времени координаты тоже любой элементарной частицы, имеющей массу покоя, будут равны:
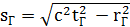 или
или 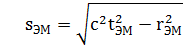
, где rГ, tГ и sГ – соответственно радиус-вектор, время движения и интервал частицы, участвующей, например, в гравитационном взаимодействии;
rЭМ, tЭМ и sЭМ – те же координаты, но частицы, участвующей в другом, допус-тим, в электромагнитном взаимодействии.
По Вейлю, законы квантовой теории поля (любого!), как уравнения, описывающие движение частиц, участвующих в разных фундаментальных взаимодействиях, не должны менять свой математический вид (остава-ться симметричными) при подстановке в них, как аргументов, пространст-венно-временных координат – r, t, s – любых подобных частиц. Но при этом для выполнения условия инвариантности данных уравнений подставляемому в них произвольному сочетанию аргументов – rГ, tГ, sГ или rЭМ, tЭМ, sЭМ (см. выше) – должна соответствовать некая компенсирующая данную произвольность величина, включаемая в уравнения поля соответствующего фундаментального взаимодействия – гравитационного, электромагнитного или какого-либо иного – в виде дополнительного слагаемого (члена). Аналогию можно провести с известным всем законом сообщающихся сосудов – выполнение да-нного закона (соблюдение условия симметричности уравнений поля) обес-печивается тем, что любому изменению уровня жидкости в одной части U-об-разной стеклянной трубки (произвольному сочетанию параметров простран-ства-времени r, t и s) соответствует адекватное изменение её уровня в другой части этой же трубки («уравновешивающее» данную произвольность дополнительное слагаемое, появляющееся в этих уравнениях).
С подачи Вейля изменения масштабов длины r и длительности t получили название калибровочных преобразований пространства-времени, а свойство уравнений квантовой теории поля сохранять неизменной свою математическую форму по отношению к этим преобразованиям – калибровочной симметрии(инвариантности) этих уравнений (т.е. симметрии, связанной со свойствами элементарных частиц, а не со свойствами пространства-времени, см. табл. 2.2). Революционным же теоретическим следствием из этой новой симметрии законов физики стало обоснование существования ве-кторных полей, квантами которых элементарные частицы обмениваются, реализуя то или иное фундаментальное взаимодействие. Указанное следст-вие, как новое свойство этих частиц, и есть смысл дополнительного слагаемого, появляющегося в данных законах с целью обеспечить их такую же новую, т.е. калибровочную симметрию. Отсюда следует вывод, предопределив-ший, ни много, ни мало, направление развития физики на весь сегодняшний (четвертый) этап истории науки – все существующие в природе фундаментальные взаимодействия (гравитационное, электромагнитное, сильное и слабое, см. тему 1.6) можно теоретически описать единым образом, а именно, как конкретные векторные квантовые поля, соответствующие своим калибровочным пространственно-временным преобразованиям. Проще говоря, сложнейшую задачу познания сущности сил, обеспечивающих целостность и устойчивость нашего мира (там же) современная физика сводит к поиску калибровочных симметрий, которыми обладают поля тех или иных таких сил (фундаментальных взаимодействий в природе), а точнее, уравнения, описыва-ющие природу этих полей. Насколько же преуспела наука второй половины 20 века в решении данной задачи? Логику событий можно изложить следую-щим образом.
Важнейшим результатом предыдущего, третьего этапа развития естест-вознания (см. тему 1.3) была волновая функция австрийского физика Э. Шредингера – уравнение, описывающее движение элементарных частиц с учетом их двойственной, корпускулярно-волновой (см. тему 1.4) природы. По мнению физиков, уравнение Шредингера в квантовой механике имеет такое же значение, как три закона Ньютона в механике классической и система уравнений Максвелла в классической же электродинамике. Так вот, калибровочные преобразования пространства-времени по отношению к волновой функ-ции, описывающей движение конкретной элементарной частицы – электро-на – позволили теоретически обосновать сущность электромагнитного взаимодействия как поля, обладающего тоже конкретным числом калибровочных симметрий, в данном случае, двух. Научная значимость этого результата заключается в том, что основываясь на знании только этих двух симме-трий, можно чисто теоретически, не проведя ни единого эксперимента по электричеству и магнетизму, получить все известные сведения о данном фундаментальном взаимодействии, а именно:
– что оно переносится квантами, не обладающими массой покоя (фотонами);
– что оно является близкодействующим;
– что существуют электромагнитные волны, способные порождать самих себя и распространяться в пустоте со скоростью света;
– что свет имеет электромагнитную природу и существует невидимая часть спектра электромагнитного излучения;
– что для участвующих в электромагнитном взаимодействии частиц (элект-ронов) выполняется закон сохранения электрического заряда;
– что, опираясь на эти калибровочные симметрии, можно теоретически опять же вывести все известные к данному моменту времени законы элект-ромагнетизма, в том числе, построить систему уравнений Максвелла и т.д.
Стоит вдуматься – учение об электромагнетизме складывалось столетиями на основе кропотливых эмпирических исследований великих экспериментаторов – Фарадея, Кулона, Ампера, Эрстеда и других – а оказывается, можно получить эти результаты, вообще не прибегая к эмпирическому этапу научного метода (см. тему 1.2) путем выявления и исследования калиброво-чной инвариантности. Сейчас электромагнитное поле, как калибровочное, является объектом изучения новой науки – квантовой электродинамики, которая, согласно принципу соответствия (см. тему 1.3), представляет собой симбиоз классической электродинамики, как теории макроскопического электро-магнитного взаимодействия, и теории взаимодействующих заряженных движущихся микрочастиц (квантовой механики).
Полученный результат совершенно естественно и логично ставил следующий вопрос – а не свойственна ли калибровочная инвариантность полям остальных фундаментальных взаимодействий – слабого, сильного и гравитационного – и если да, то может быть именно с её помощью (как, собст-венно и предлагал Вейль, см. выше) можно решить проблему, перед которой отступил сам Эйнштейн? Столь грандиозную задачу современная физика ре-шает (именно решает, поскольку данная работа еще не завершена) тоже совершенно понятным образом – волновая функция Шредингера, как уравнение, описывающее поведение всех элементарных частиц, «грузится» все более сложными калибровочными преобразованиями пространства и времени с тем, чтобы, с одной стороны, доказать калибровочный характер полей всех фундаментальных взаимодействий, а с другой – установить наличие связи между ними. На сегодняшний итоги реализации данной научной программы таковы (рис. 2.9):
| спонтанное нарушение симметрии электрослабого взаимодействия |
| спонтанное нарушение симметрии более фундаментального взаимодействия |
| спонтанное нарушение симметрии супервзаимодействия |
| Гравитационное взаимодействие – разновидность супервзаимодействия с ненарушенной симметрией |
| Более фундаментальное взаимодействие – разновидность супервзаимодействия с нарушенной симметрией |
| Электромагнитное взаимодействие – разновидность электрослабого взаимодействия с ненарушенной симметрией |
| Слабое взаимодействие – разновидность электрослабого взаимодейст-вия с нарушенной симметрией |
| Сильное взаимодействие – разновид-ность более фундаментального взаимодействия с ненарушенной симметрией |
| Электрослабое взаимодействие – ра-зновидность более фундаментального взаимодействия с нарушенной симметрией |
| Супервзаимодействие (супергравита-ция) с ненарушенной суперсимметрией |
Рис. 2.9. Сценарий объединения фундаментальных взаимодействий
Дата: 2019-02-02, просмотров: 344.