Формирование новых представлений о пространстве и времени шло по сценарию, схожему со становлением квантовой концепции материи (см. тему 1.4). Так, подобно тому, как Планк новый закон излучения предложил сначала в виде эмпирической зависимости (там же), точно так же его коллеги физики в качестве первого шага формирования данных представлений попытались сначала просто дать математическую интерпретацию результата опыта Майкельсона – Морли. Это сделал нидерландский физик Хендрик Лоренц, задавшись целью «примирить» результат данного опыта с преобразованиями Галилея, т.е. сделать инвариантными к ним не только законы поведения вещества (законы механики Ньютона), но и законы поведения поля (законы электродинамики Максвелла). В 1904 году он, подобно Планку, предложил систему тоже эмпирических зависимостей – преобразований параметров пространства и времени, названную впоследствии Эйнштейном в знак уважения к ученому «преобразованиями Лоренца», при использовании которых вместо преобразований Галилея для перехода от одной инерциальной системы отсчета к другой (см. рис. 2.1) инвариантность законов поля обеспечивалась. Но по отношению к другому виду материи – веществу (носителю электрического заряда, который при движении тела это поле создает) – преобразования Лоренца предполагали нечто новое и совершенно невероятное – что будто бы все подобные тела, включая Землю, реально сокращаются в размерах в направлении своего прямолинейного движения под действием возникающих при этом электромагнитных сил, причем величина данного сокращения прямо пропорциональна скорости движения тела. Мало того, в прямой же зависимости от этой скорости оказывается величина замедления времени для движущегося тела.
Для инерциальных систем, показанных на рис. 2.1 (см. выше), преобразования Лоренца имеют следующий вид:
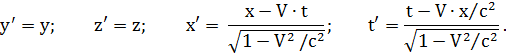
В качестве примера можно, используя приведенные зависимости, подсчитать, что ракета длиной, допустим, x = 50 м при скорости своего движения V = 100 км/с сокращает свою длину по отношению к Земле, с которой взлетела, на 0,003 мм в направлении этого движения, а часы, установленные в ракете, будут идти на 0,00002 с медленнее часов, установленных на Земле и синхронизированных с первыми в момент старта ракеты. Можно также убедиться, что для земных условий, где V много меньше c, а, следовательно, отношение V/c стремится к нулю, преобразования Лоренца, как это и положено по принципу соответствия Н. Бора (см. тему 1.3), вырождаются (упрощаются) в преобразования Галилея (см. тему 2.1).
Заканчивая аналогию между описываемыми событиями и разрешением «ультрафиолетовой катастрофы» (снова см. тему 1.4), уточним, что, как и закон излучения Планка, преобразования Лоренца не были даже гипотезой, поскольку никаких разумных и логичных теоретических объяснений причин уменьшения размеров движущихся тел и замедления для них хода времени они не давали – получается, что это такой же «фокус аппроксимации», каковым современники первоначально сочли выше упомянутый закон (там же). Отличие же в том, что подобные объяснения Планк дал, как известно, сам – в виде квантовой гипотезы. Смысл же преобразований Лоренца, а также результат опыта Майкельсона – Морли и ему (Лоренцу), и всему миру объяснил другой человек. Это сделал 26-тилетний (!) Альберт Эйнштейн в статье «К электродинамике движущихся тел», опубликованной в сентябре 1905 г. в немецком научном журнале «Анналы физики».
Данная статья явилась итогом почти десятилетних размышлений Эйнштейна, как он сам выражался, «о соотношении между твердыми телами (координатными системами), часами и электромагнитными процессами (скорос-тью света)». Важнейший вывод этих размышлений, считающийся главной су-тью изложенных в выше упомянутой статье основ специальной теории относительности – относительность одновременности. Смысл данного понятия, полностью пересматривающего ньютоновские представления о прост-ранстве и времени, заключается в следующем.
Согласно рис. 2.3, система отсчета x ', y ' движется относительно сис-темы отсчета x , y с постоянной скоростью V вдоль оси x. В точке О происходит вспышка света. Наблюдатель, находящийся в системе отсчета x, 'y', ра-ссуждает следующим образом – скорость света c в направлениях ОА и ОВ одна и та же, а поскольку по определению ОА = ОВ, свет достигает точек А и В одновременно.
Наблюдатель, находящийся в системе отсчета x, y, рассуждает в той же теоретической манере, что и его коллега из системы отсчета x', y', но приходит к совершенно иному выводу – скорость света c действительно одинакова
| x |
| x' |
| y' |
| y |
| В |
| с |
| О |
| с |
| А |
| V = const |
Рис. 2.3. Относительность одновременности
в направлениях ОА и ОВ, но для меня точка А к источнику света (точке О) приближается, а точка В от этого же источника удаляется, в результате чего свет окажется в точке А раньше, чем в точке В. Получается, что события, одновременные в системе отсчета x ', y ', оказываются неодновременными в системе отсчета x , y, следовательно, одновременность – понятие относительное. Наблюдатели, движущиеся относительно друг друга, будут иметь различные мнения об одновременности одних и тех же событий – события, являющиеся одновременными для одного наблюдателя, не одновременны для другого наблюдателя, движущегося относительно первого.
Из относительности одновременности следует относительность размера тела в направлении его движения – ведь чтобы измерить длину тела, необходимо отметить левую и правую границу этой длины одновременно, а это, как только что было доказано, невозможно. Выходит, и длина тела, измеренная разными наблюдателями, которые движутся друг относительно друга, тоже должна быть различна.
В таком новом понимании промежутки времени и размеры тел теряют абсолютный характер, какой им приписывался классической физикой (см. тему 2.1), и приобретают статус относительных величин, зависящих от вы-бора системы отсчета, с помощью которой проводилось их измерение – пространство и время получаются неразрывно связанными с движением наб-людателя и объекта наблюдения друг относительно друга. На основании да-нного вывода истинный смысл преобразований Лоренца их автору и всем остальным Эйнштейн разъяснил так. В этих преобразованиях отражается не реальное изменение размера движущегося тела и не имеющее место в дейст-вительности замедление для него хода времени (опять «детские» вопросы – куда, скажем, «пропали» 0,003 мм длины летящей ракеты из выше приведенного примера, они «отрастут» обратно, если ракета остановится, или нет?), а изменение результатов измерения данных параметров движения тела в зависимости от того, в какой из систем отсчета – подвижной или неподвижной – эти измерения производятся. Проще говоря, то, что видит наблюдатель, определяется тем, где он находится. В таком контексте разница в природе полей, возникающих в подвижной и неподвижной системах отсчета (см. тему 2.1), вполне допустима и объяснима. Эйнштейн усмотрел в преобразованиях Лоренца математическое выражение открытого им нового качества пространства и времени – быть зависимыми и связанными с движением по отношению к ним материальных объектов – макроскопических тел как механических систем, содержащих электрические заряды, поскольку любое вещество состоит из заряженных частиц. Если учесть, сказал он, это новое качество форм существования материи заменой преобразований Галилея (отказом от ньютоновских представлений о пространстве и времени) преобразованиями Лоренца (принятием других, постньютоновских представлений о них), то принцип относительности Галилея оказывается справедлив не только по отношению к механическому движению, но и по отношению к электромагни-тным явлениям. Тогда он утрачивает статус закона классической механики, приобретая статус более общего закона физики – принципа относительности. Именем Эйнштейна, по аналогии с принципом относительности Галилея, его называть, на наш взгляд, не совсем корректно, поскольку за год до выше упомянутой публикации Эйнштейна, т.е. в 1904 г., данный закон сформулировал другой ученый – французский математик Анри Пуанкаре.
Для наглядности факта соблюдения принципа соответствия Н. Бора (см. тему 1.3) формулировки принципа относительности Пуанкаре – Эйнш-тейна приводим в тех же оборотах речи, что и суть принципа Галилея (см. тему 2.1):
· все физические (теперь, в начале 20 века – не только механические, но и электромагнитные, а именно, оптические, тепловые и др.) процессы про-текают одинаково во всех инерциальных системах отсчета;
· законы электродинамики инвариантны к преобразованиям Лоренца (напомним, что для одного из частных случаев этих преобразований, а именно, при отношении V/c, стремящемся к нулю, к ним инвариантны и законы механики, см. выше).
Еще одно новое качество пространства и времени, обнаруженное опытом Майкельсона – Морли (см. тему 2.1), Эйнштейн предложил зафиксировать в виде принципа постоянства скорости света, гласящего, что скорость света в вакууме c одинакова во всех инерциальных системах отсчета и не зависит от движения источников и приемников света, причем дополнил данный принцип положением о невозможности распространения вообще какого-либо физического взаимодействия со скоростью, бóльшей, чем скорость света.
Данные два принципа – принцип относительности Пуанкаре – Эйнш-тейна и принцип постоянства скорости света – являются постулатами специальной теории относительности А. Эйнштейна (1905 г.). Специальной она называется потому, что, будучи новой теорией, более сложно и достоверно, чем теория старая (классическая механика) описывающей движение тел, она не учитывала источник этого движения – энергию гравитации (силу тяготения). Иными словами, кинематику Ньютона (как двигаются тела) Эйнштейн на «язык» специальной теории относительности «перевел», а динамику Ньютона (почему, под действием какой силы тела двигаются) он «переведет» на «язык» другой, уже универсальной или общей теории относительности, но это будет позже (см. тему 2.3), пока же необходимо было прос-то объяснить происхождение названия теории, о которой идет речь в насто-ящем разделе. Как принципиально иная, нежели механика Галилея – Нью-тона, специальная теория относительности имеет ещё название релятивистской (см. тему 1.3) механики, поскольку в ней, действительно, переменными и относительными, т.е. релятивистскими стали параметры пространства, времени и движения тел.
Еще одним принципиально новым положением специальной теории от-носительности стала отмена господствовавшего в механике Ньютона принципа дальнодействия (см. тему 1.3), поскольку, в соответствии с постулатом постоянства скорости света (см. выше), все возможные физические взаимодействия квалифицируются только как близкодействующие. В этой связи новый вид и новую сущность в специальной теории относительности приобретает правило сложения скоростей движения тела. Если, согласно рис. 2.1, тело движется вдоль осей x и x' со скоростями v и v' соответственно, то
v = ( v' + V ) / ( 1 + V ∙ v' / c2 ) .
Для самого предельного случая, когда и скорость движения V подвижной системы отсчета вдоль оси x, и скорость движения тела v' вдоль оси x' данной системы равны скорости света c, кажется, что по закону сложения скоростей классической механики относительно оси x тело будет двигаться с суммарной скоростью v = V + v' = c + c = 2c. Отнюдь:
v = ( c + c ) / ( 1 + c ∙ c / с2 ) = 2с / 2 = c .
Опять же для земных условий, когда скорости V и v' во много раз мень-ше скорости света c, величиной V∙v'/c2, как стремящейся к нулю, можно пре-небречь, и релятивистская формула сложения скоростей движения тела выро-ждается в соответствующую формулу механики Ньютона:
v = v' + V .
Также релятивистской, т.е. тоже зависящей от скорости движения тела V, становится его масса m':
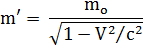
, где m0 – масса тела в неподвижной системе отсчета (см. рис. 2.1), или его масса покоя, которой, как постоянной, не зависящей от скорости движения тела, оперирует классическая механика.
Поскольку скорость V является мерилом кинетической энергии (энергии движения) тела, то из выше приведенной формулы следует факт сущест-вования связи между массой и энергией вещества. К моменту создания специальной теории относительности уже были известны результаты исключительно тонких опытов русского ученого Петра Николаевича Лебедева по доказательству существования и измерению величины давления света, падаю-щего на поверхность тела. Как частный случай существования выше указан-ной связи, Лебедев получил эмпирическую зависимость (см. тему 1.2), согла-сно которой давление света пропорционально квадрату его скорости. Опираясь на результаты Лебедева, Эйнштейн показал, что между полной энергией тела E (аналог внутренней энергии, см. тему 1.5) и его массой m существует универсальная зависимость вида E = mc 2, которая считается самой знаменитой формулой в мире, или «формулой 20 века» (она высечена на кенотафе Эйнштейна, установленном на кладбище города Принстон, США). Почему? С научной точки зрения значимость этой формулы в том, что она доказала единство двух видов материи – вещества и поля – что является важнейшим результатом целого этапа развития науки – этапа неклассического естествоз-нания (см. тему 1.3). Кроме того, энергия Е в данной формуле – это вовсе не энергия движения массой m (как функции данного аргумента), а максимальная запасенная этой массой энергия. Полностью, без остатка превратиться в какую-либо полезную энергию (например, в энергию излучения) она может только в результате аннигиляции частиц и античастиц (см. тему 1.4). В этом контексте формула Эйнштейна приобретает колоссальное экономическое (хозяйственное) значение, поскольку выражает собой полное и окончательное решение столь актуальной сейчас проблемы ресурсосбережения – сколько энергии E можно получить из энергоносителя массой m при максимально полном полезном его использовании (КПД = 100%). Русский и советский физик С.И. Вавилов подсчитал, что энергия, получаемая всей нашей Землей от Солнца за одну секунду эквивалентна, по Эйнштейну, двум (!) килограммам вещества (любого). Можно привести пример более прагматичный – энергия покоя 1 кг вещества равна количеству энергии, потребляемой сейчас такой страной, как США, за неделю (!). Это в теории, а на практике что? КПД сов-ременной тепловой энергетики, т.е. той, которая работает на сжигании органического топлива, составляет всего 10-8 %, поскольку энергия химической связи атомов в молекуле (а именно она высвобождается при горении) составляет как раз такую мизерную величину от полной, по Эйнштейну, энергии Е этих атомов. В этом смысле формула века являет собой математическое подтверждение слов другого русского ученого – Д.И. Менделеева, который задолго до Эйнштейна сказал, что топить печь углем – это все равно, что топить печь банкнотами. Для сравнения – в атомной энергетике КПД, т.е. доля высвобождаемой энергии процессов деления ядер урана от той же полной их энергии Е, равен 0,1% (больше в десять миллионов раз!). В силу этого альтернативы атомной энергетике нет, тем более, что превратить всю запасе-нную в веществе энергию в полезную принципиально нельзя, поскольку унич-тожить образующие его протоны и нейтроны мы не можем.
Остается добавить, что с учетом выражения для релятивистской массы m' (см. выше) формула Эйнштейна имеет вид:
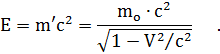
Формирование математического аппарата специальной теории относительности завершил в 1908 году немецкий физик, учитель Эйнштейна по математике Герман Минковский. Он объединил считавшиеся в ньютоновской механике существующими отдельно друг от друга пространство и время в единое четырехмерное «пространство-время», или в пространственно-вре-меннóй континуум. У Ньютона любое тело, рассматриваемое как материальная точка (см. тему 1.3), имеет две независимые координаты – расстояние от начала отсчета трехмерной (декартовой) системы координат xyz до данной точки, или её радиус-вектор r:
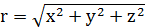
и время движения t этой же точки, измеряемое по другой, уже одномерной оси – оси времени, естественно. По Минковскому же мир представляет собой плоское четырехмерное пространство-время, в котором положение любого материального объекта (как будет показано ниже, уже не только тела, но и поля!) и его перемещения характеризуются одной величиной, называемой интервалом (или мировым интервалом, а также мировой линией) s:
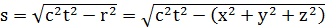
, который характеризует расстояние до той точки-события этого четырехмерного континуума, где находится данный материальный объект. При этом временные и пространственные координаты не отождествляются, а, на-оборот, представляют собой четыре разных измерения, производимых по трем пространственным осям и по одной временнóй и «размеченных» в одних и тех же единицах измерения (см. формулу). Термин «плоское» в вышеприведенном названии этого единого пространства-времени указывает на то, что, с одной стороны, в этом новом симбиозе пространство осталось евклидовым. Забегая вперед, скажем, что неевклидовым, или искривленным, оно станет позже, в другой, более сложной теории относительности – в общей (см. тему 2.3). Но, с другой стороны, чисто евклидовым, как у Ньютона (см. тему 2.1) пространство все-таки уже не является, поскольку, говоря по-про-стому, «вошло» составной частью в некое бóльшее целое совершенно иной природы. Чтобы подчеркнуть эту разницу, тот же Минковский предложил на-зывать интерпретируемое им выше описанным образом пространство псевдоевклидовым.
Введение Минковским понятия интервала s позволило получить мате-матическую интерпретацию первого постулата специальной теории относительности (принципа относительности Пуанкаре – Эйнштейна, см. выше) в виде Δ s = Δ s ', что означает – в инерциальных системах отсчета величина изменения интервала Δ s = s 1 – s 2 остается неизменной (абсолютной) для любых двух точек-событий s 1 и s 2. Более коротко это означает, что в специальной теории относительности инвариантом является изменение интервала между двумя точками-событиями. Абсолютная же величина интервала s, выступающая единой координатой любого материального объекта в четырехмерном пространстве-времени (см. выше), определяется величинами соответствующих своих составляющих – пространственной r и временнóй t – как аргументов (там же).
Кроме того, если в формуле Минковского положить r = 0, то интервал s становится пространственно-временным параметром поля. Действительно, размеров (координат) x, y или z поле не имеет, и скорость его распространения может быть только скоростью света в любой системе отсчета, т.е. для него соотношение Δs = Δs' тоже выполняется. Данное следствие примечате-льно тем, что справедливость представлений специальной теории относите-льности для обоих видов материи – и вещества, и поля – доказывается не постулатами (напомним, что постулат – это исходное утверждение, принимаемое без доказательств), а строгим математическим выводом.
С учетом введенных Минковским понятий суть всей специальной теории относительности предельно кратко (наибольшая степень сворачивания информации, см. тему 1.2) можно выразить так – инвариантами специа-льной теории относительности являются изменение интервала Δs и скорость света в вакууме c .
Также математически строго из специальной теории относительности выводятся так называемые релятивистские эффекты:
Ø движущиеся часы идут медленнее часов покоящихся. По аналогии со следствиями из преобразований Галилея (см. тему 2.1), это означает, что t > t', т.е. для движущегося тела время t', измеренное в системе отсчета движущейся с этим телом, течет медленнее (оно меньше), чем время t, измеренное в неподвижной системе отсчета;
Ø размер тела сокращается в направлении его движения. В тех же следс-твиях (см. выше) данный размер – это Δx = x2 – x1. Тогда математически данный релятивистский эффект выражается неравенством Δx < Δx', т.е. размер Δx движущегося тела, измеренный в неподвижной по отношению к нему системе отсчета, меньше, чем размер Δx' этого тела, измере-нный в системе отсчета движущейся вместе с ним;
Ø масса движущегося тела (релятивистская масса) больше массы тела покоящегося (массы покоя тела). В принятых выше обозначениях это записывается неравенством m' > m0 , т.е. масса m' движущегося тела, измеренная в неподвижной по отношению к нему системе отсчета, больше, чем масса m0 этого тела, измеренная в движущейся вместе с ним системе отсчета;
Ø события, одновременные в одной системе отсчета, не являются одновременными в системе отсчета, движущейся относительно первой (от-носительность одновременности, см. выше).
Общим для трех первых выше приведенных релятивистских эффектов является положение о невозможности достижения телом скорости света (см. выше). Это означает, что в преобразованиях Лоренца и в формуле для определения релятивистской массы (там же) предельный случай в виде V = c (или, что то же самое, V/c = 1) допускается только теоретически. Более того, в земных условиях реальная скорость перемещения тел даже не соизмерима со скоростью света. Так, если вспомнить, что только весьма немногие из современных транспортных средств имеют скорость, равную скорости звука (а это всего лишь 340 м/с), то даже для них V/c = 0,34/300 000 есть бесконечно малая величина. Именно поэтому, как это уже было отмечено в отношении корпускулярно-волнового дуализма (см. тему 1.4), релятивистские эффек-ты на Земле незаметны. Мы здесь опять имеем дело с проблемой нагляд-ности физических представлений о реальности – действительно, ну как обы-вателю объяснить, что такое, например, единое пространство-время? Можно, конечно, воспользоваться метафорой И. Бродского, что тюрьма – это ограничение в пространстве, компенсируемое увеличением во времени, но это не наука, а шутка Нобелевского лауреата по литературе.
Данная проблема является естественным следствием прогресса науки в целом, и особенно физики – создавая все более сложные и, в силу этого, все более достоверные формы научного знания (см. тему 1.2), она вынуждена постепенно отказываться от его непосредственной наглядности. Подобная тенденция, как может показаться, противоречит самой сути научного метода, согласно которому, современная наука, и физика, прежде всего, основываются на эмпирическом опыте, т.е. на данных наблюдения и на результатах эксперимента (там же). Но дело в том, что реальность, как уже говорилось, сложна бесконечно, и потому некоторые её стороны просто недоступны для эмпирического исследования. В этом случае, наоборот, доступность тех сторон реальности, которые все же поддаются непосредственному наблюдению или моделированию, может привести к неверной трактовке её сути в силу неполноты исходной информации. Так, динамика Аристотеля базировалась на не раз уже упоминавшемся принципе, что движущееся тело останавливается, если сила прекращает свое действие на него. Этот принцип казался соответствующим реальности и здравому смыслу только потому, что не замечалось, что причиной остановки тела является трение. И понадобился другой, уже мысленный эксперимент Галилея с несуществующими, т.е. не являющихся наглядными инерциальными системами отсчета (см. рис. 2.1), чтобы дать более правильную трактовку реальности – что если ничто не будет влиять на движение тела, оно (движение) может продолжаться бесконечно долго (иная, нежели в теме 2.1, редакция принципа относительности Галилея). Да что там Галилей – последние сомнения в том, что Земля действите-льно шар, исчезли только после получения во второй половине 20 века её фотографий с околоземной орбиты – настолько такие представления противоречили тому же здравому смыслу. В этом контексте уместно будет привести высказывание Эйнштейна по поводу тех, кто не верил в действительно казав-шиеся невероятными выводы его теории: «Здравый смысл – это предрассудки, которые складываются в возрасте до восемнадцати лет».
Таким образом, характерной чертой именно третьего этапа истории естествознания, которую можно считать дополнительной к описанным в теме 1.3 тенденциям развития науки, является её (науки) отказ не только от непосредственной наглядности своих трактовок реальности, но и от нагляд-ности научных представлений вообще. Отсюда вопрос – как же доказывать правоту таких объяснений, если они не являются наглядными, а потому кажутся неубедительными и даже фантастическими? Ответ известен. Сутью нау-чного метода был и остается тезис «Практика – критерий истины» (первая тенденция развития естествознания, там же), поэтому эмпирическое подтверждение существования каких-либо недоступных для непосредственного восприятия в данной конкретной области реальности её свойств надо искать в других областях этой же реальности, где данные свойства поддаются наблюдению или моделированию. Почему такой путь познания возможен – потому, что материя едина (см. тему 1.4), но в разных областях реальности структурирована также по-разному, следовательно, можно предположить, что доступность или недоступность для обнаружения и доказательства существования тех или иных свойств реальности в разных областях этой реальности выражены неодинаково. Так, неочевидные для земной реальности предста-вления о форме нашей планеты были подтверждены наблюдениями из-за пределов этой реальности, т.е. из космоса (см. выше). Такая же «незаметная» в земных условиях двуединая вещественно-полевая сущность материальных образований была доказана экспериментом в другой области их существования – в мире элементарных частиц (опыт Дэвиссона – Джермера, см. тему 1.4). По-добным же образом дело обстояло и с получением эмпирических фактов, подтверждающих правоту специальной теории относительности.
Релятивистское замедление времени подтверждается следующими многократно зафиксированными наблюдениями. В космических лучах, проника-ющих в верхние слои атмосферы (а это более 10 км от поверхности Земли), образуются элементарные частицы, называемые пи-мезонами, или мюонами. Будучи по природе своей короткоживущими, нестабильными и самопроизвольно распадающимися, они имеют собственное время жизни около 2 ми-кросекунд. За это время, двигаясь со скоростью, соизмеримой со скоростью света (примерно 0,5 с), они могут пролететь не более 300 м. Именно такой путь мюонов регистрируют приборы, установленные на воздушных шарах, запускаемых в верхние слои атмосферы с научными целями. Такие же приборы, расположенные на поверхности Земли регистрируют эти же частицы как долетевшие до нас и прошедшие путь, равный 30 км, т.е. в 10 000 раз бóльший, чем для них возможно. Специальная теория относительности так объясняет данный факт: время t' = 2 мкс является временем, измеренным по часам, движущимся вместе с мюоном, т.е. находящимися, как и последний, в подвижной системе отсчета. В системе же отсчета, связанной с Землей, т.е. в неподвижной, время жизни этой же частицы t намного больше, что соответствует релятивистскому эффекту t > t' (см. выше).
В 1971 г. в США был поставлен эксперимент по доказательству замедления времени не только по отношению к элементарным частицам, как в выше описанном случае, но и для макроскопических тел, т.е. для условий не ко-смической, а земной реальности. Изготовили двое совершенно одинаковых точных часов. Одни часы оставались на Земле, а другие помещались в самолет, который летал вокруг Земли. Самолет, летящий по круговой траектории, движется с некоторым ускорением по отношению к вращающейся вокруг своей оси Земле, и значит, часы на борту самолета находятся в другой ситуации по сравнению с часами, покоящимися на её поверхности. Предварительные расчеты с помощью преобразований Лоренца показали, что часы-путе-шественники должны были отстать от часов покоящихся на 184 наносекунды, а на самом деле отставание в выше приведенных обозначениях составило t – t' = 203 нс. Превышение фактического результата эксперимента над расчетным объяснили тем, что движение самолета по отношению к Земле, как подвижной системы отсчета относительно неподвижной, было все-таки не в полной мере прямолинейным и равномерным.
Не данными наблюдения или эксперимента, как в двух предыдущих случаях, а теоретическим следствием, вытекающим из релятивистского замедления времени, который в свое время вызывал наиболее многочисленные споры и недоразумения, является предложенный самим Эйнштейном так называемый «парадокс близнецов». Допустим, что этим близнецам по 25 лет, и один из них отправляется в космический полет, а другой остается на Земле. Если во время этого полета скорость космического корабля была близкой к скорости света с (например, 0,99 с), и вернулся он на Землю через 50 лет, то, согласно Эйнштейну, по часам этого корабля полет продолжался бы всего лишь около 7 лет. В результате при встрече остававшийся на Земле 75-лет-ний близнец будет приветствовать своего 32-летнего брата. Подчеркнем, что «парадокс близнецов» – это реальный эффект: путешествующий близнец стареет медленнее, чем оставшийся на Земле его брат. Замедление времени позволяет нам вообразить заманчивую возможность путешествовать к далеким звездам. Если такое путешествие будет совершаться со скоростью, близкой к скорости света, то космонавты смогут преодолевать громадные расстояния за время, достаточно малое по сравнению со временем человеческой жизни. Именно поэтому «парадокс близнецов» является наиболее известной научно-популярной и художественной иллюстрацией к специальной теории относительности и по сей день. Однако эти фантазии являются абсолютно беспочвенными, потому что на самом деле «парадокс близнецов» не содержит никакого парадокса по одной простой причине – система отсчета, связа-нная с путешествующим космическим кораблем, не является инерциальной, поскольку испытывает ускорение вместе с этим кораблем при его повороте назад, к Земле, как к неподвижной системе отсчета.
По поводу практического доказательства остальных релятивистских эффектов можно добавить, что в литературе есть сведения об экспериментах с элементарными частицами, подтверждающие увеличение массы этих частиц с возрастанием их скорости. Так, в современных ускорителях электрон разгоняется до скорости 0,9999999 с. С точки зрения наблюдателя его масса при этом должна увеличиться в 2 500 раз, но подтвердить данный результат расчета измерениями пока не удается. Более того, по отношению к макроскопическим телам есть расчеты, показывающие, например, что нагрев тонны воды с нуля до 100оС увеличивает её вес приблизительно на 0,005 мг, пос-кольку, в полном соответствии с молекулярно-кинетической теорией (см. тему 1.5), возрастает скорость движения молекул воды. Но как вскипятить и взвесить с точностью до тысячной доли миллиграмма тонну воды?
Релятивистское правило сложения скоростей (а, следовательно, и второй постулат специальной теории относительности) также подтверждены как астрономическими наблюдениями, так и сугубо земными экспериментами. Так, в глубинах космоса существуют так называемые «двойные звёзды» – ус-тойчивые системы, в которых две звезды с колоссальной, по земным меркам, скоростью вращаются вокруг общего центра их масс, уравновешивая этим вращением свое взаимное притяжение (рис. 2.4). Согласно представлениям
| VA |
| c + VA |
| К наблюдателю |
| с − VB |
| VB |
| Центр масс |
| Звезда В |
| Звезда A |
Рис. 2.4. Галилеевское сложение скоростей в системе двух звезд
классической механики, свет от каждой из этих звезд приходил бы к нам со скоростями c + VА и c – VB (там же), что по расчетам, с учетом громадного расстояния до ближайшей системы двух звезд, составило бы по времени разницу в регистрации сигнала от обеих составляющих данной системы почти в неделю (!). Однако, данные астрономических наблюдений за подобными кос-мическими объектами всегда показывают синхронность сдвоенного сигнала, приходящего на Землю от двойных звезд, что соответствует релятивистскому, а не галилеевскому, правилу сложения скоростей и является подтверждением правоты постулата о постоянстве скорости света.
В земных условиях данный постулат был подтвержден еще до создания специальной теории относительности опытом, который поставил французский физик Арман Физо. Он задался целью определить, с какой скоростью распространяется свет в неподвижной жидкости и в жидкости, протекающей с некоторой скоростью внутри стеклянной трубки. С помощью проведенных
Физо тщательных измерений, далее многократно повторенных разными исследователями, было установлено, что скорость света в жидкости и скорость самой жидкости суммируются по релятивистскому правилу сложения скоростей (см. выше).
Хотя специальная теория относительности носит имя Альберта Эйнш-тейна, сам он всегда воздавал должное вкладу в её создание других ученых. Так, позже он напишет: «Я совершенно не понимаю, почему меня превозносят как создателя теории относительности. Не будь меня, через год это бы сделал Пуанкаре, через два года сделал бы Минковский, в конце концов, более половины в этом деле принадлежит Лоренцу. Мои заслуги преувеличены». Но коллеги – современники Эйнштейна (в частности, тот же Лоренц) – считали, что именно ему принадлежит заслуга создания законченной, строгой и всеобщей теории, столь революционно изменившей наши представления о пространстве и времени.
Дата: 2019-02-02, просмотров: 364.