Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

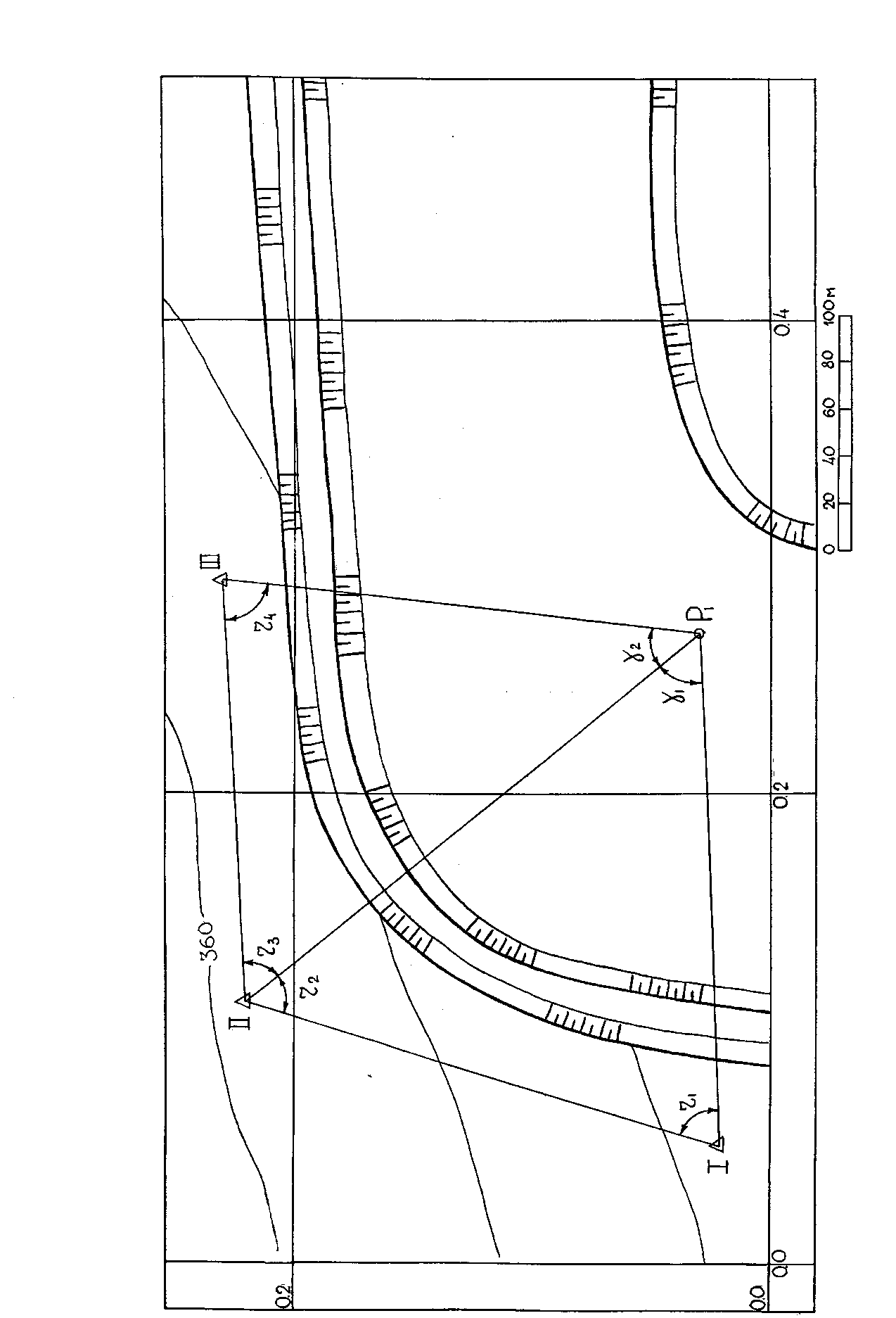
1. По аналогии с рис. 2 на листе формата А4 вычерчивается план участка карьера в масштабе 1 : 2000.

2. На план участка карьера по известным координатам X_I, Y₁, X_II, Y_II, X_III, Y_III (табл. 3) наносятся пункты опорной сетей: I, II, III.

3. В карьере на нижнем горизонте между вторым и третьим уступом выбирают место заложения точки съемочного обоснования (точка Р₁, см. рис. 2). При выборе места заложения пункта Р₁ учитываются требования, предъявляемые к геодезическим засечкам, указанные выше и в инструкции [1]. Наиболее выгодная форма – равносторонний треугольник.

 

   Таблица 3

  Координаты пунктов опорной сети

Номера пунктов	Х, м	Y, м
I II III IV	20 220 230 200	50 110 290 460

Исходные данные для расчета координат точки P₁:

углы r₁, r₂, r₃, r₄ берутся с плана, измеряются транспортиром с точностью 0,5^о (на практике они измеряются теодолитом). Дополнительно,

для повышения точности расчета и недопущения грубых ошибок измеряются углы при определяемом пункте (g₁,  g₂ ), и сумма углов в треугольнике уравнивается к 180^о 

 

;

.

 

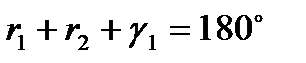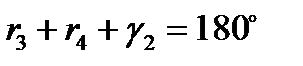Решение прямой геодезической засечки

По формулам котангенсов измеренных углов

Вычисление координат пункта Р_I

из треугольника l-ll-Р_I

Измеренные углы:   r₁=71^°,r₂=56^°, g₁=53^°.

Исходные данные:

Х_I = 20 м; У_I = 50 м; Х_II = 50 м; Х_III = 220 м; У_II = 110 м. (см. табл.2)

Решение.

=  =

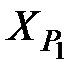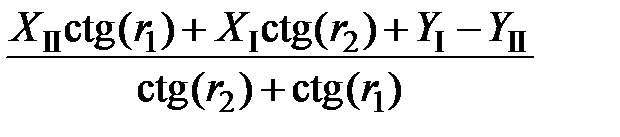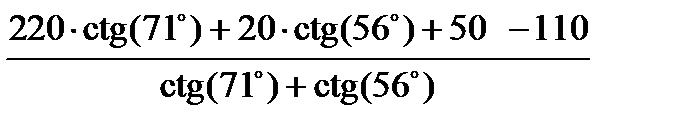=  = 28,634 м,

 

=  =

 

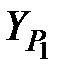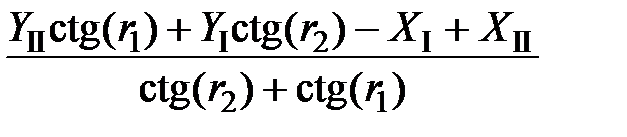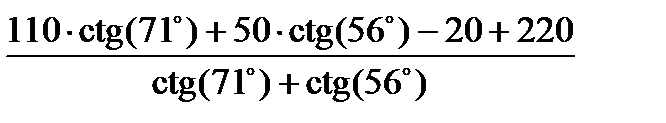=  = 266,739 м.

 

Контроль промежуточный:

X_I =  =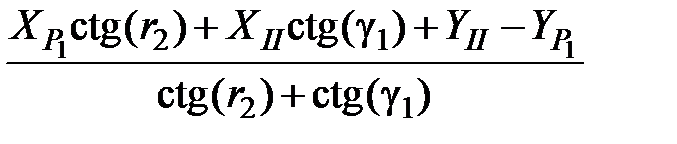

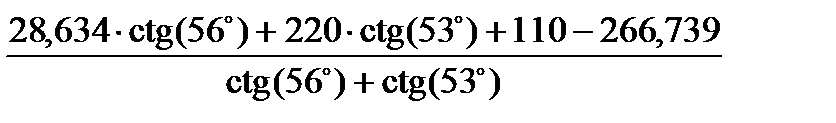 = = 19,776 м.

 

Y_I =  =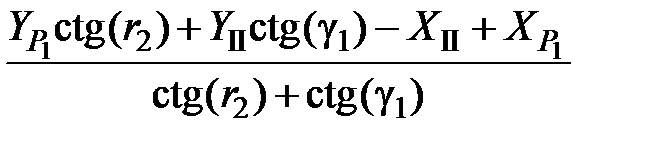

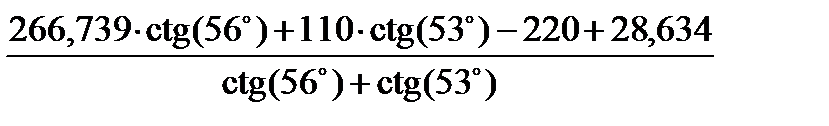= = 49,927 м.

 

Вычисление координат пункта Р₁

из треугольника ll-lll-Р₁

 

Измеренные углы: r₃=54^°; r₄=80^°; g₂=46^°

Исходные данные:

Х_II = 220 м; У_II = 110 м; Х_III = 50 м; Х_III = 230 м; У_III = 290 м. (см. табл.2)

Решение.

      

= =

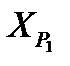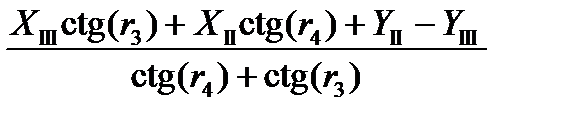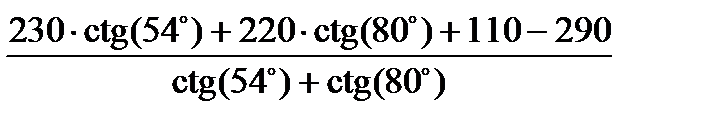= =28,711 м,

 

= =

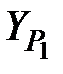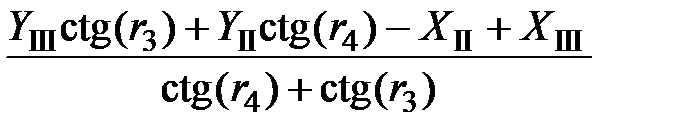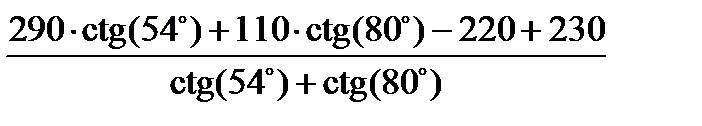= =266,178 м.

 

Контроль промежуточный:

 

 

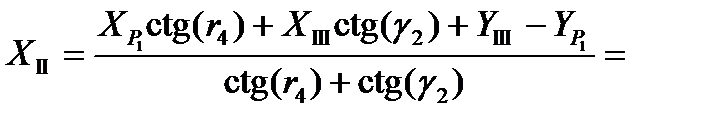
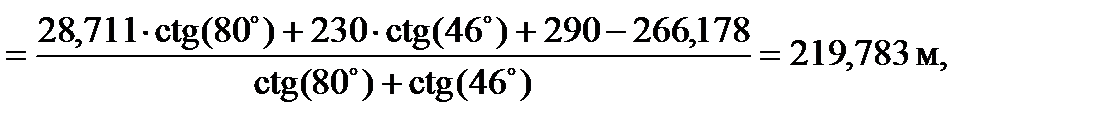
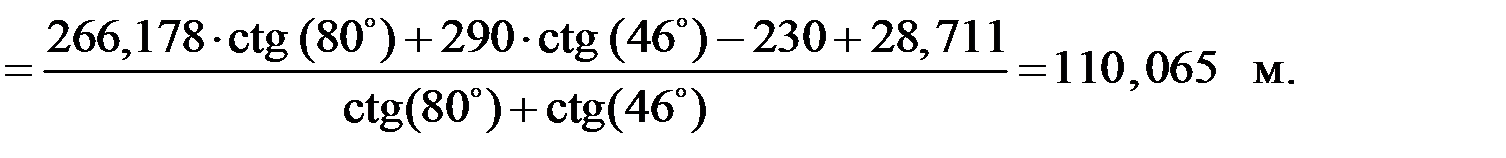
Контроль решения прямой засечки:     

Из решения двух треугольников разница в координатах пункта Р₁ составляет

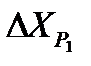 =0,077 м,  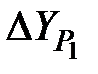   =0,561 м,

которая не превышает 0,6 мм на плане в масштабе съемки (для масштаба 1:2000 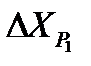, 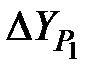£ 1,2 м).

    Среднеарифметическое значение координат точки Р₁ из двух треугольников:

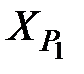 =28,672 м, 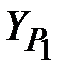=266,458 м.

Оценка точности планового положения пункта Р₁ характеризуется среднеквадратической погрешностью относительно пунктов опорной сети, величина которой не должна превышать 0,4 мм на плане в масштабе съемки [1] (для масштаба 1:2000 М_Р £ 0,8 м):

    для треугольника I-II-P₁

 

 =  =

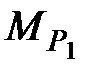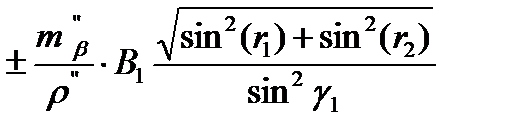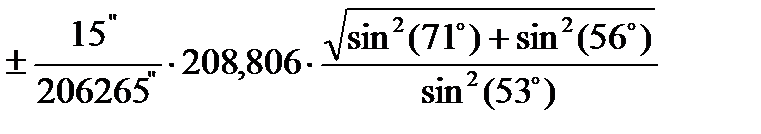=  = 0,030 м;

 

 

    для треугольника II-III-P₁

 

=  =

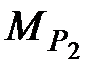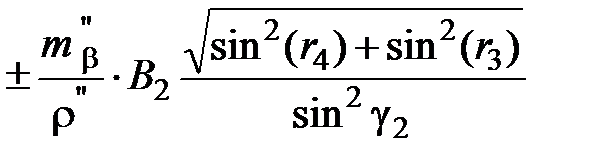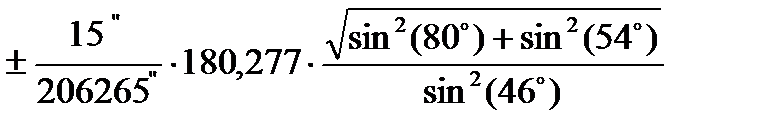=  = 0,032 м,

где 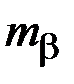- среднеквадратическая погрешность измерения углов (15^");

B₁, В₂ - базис прямой засечки (расстояние между пунктами опорной сети), определяется решением обратной геодезической задачи:

В₁ = 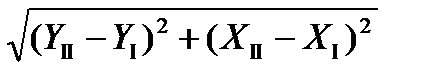= = 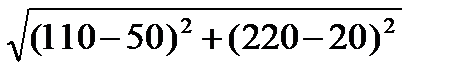208,806 м;        

 

В₂= 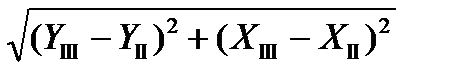=  = 180,277 м.

 

      В результате среднеквадратическая погрешность положения пункта Р₁ относительно пунктов опорной сети из двух треугольников составила 0,032 м и не превышает допустимой величины (0,8 м).

Решение прямой геодезической засечки

По формулам тангенсов дирекционных углов

Вычисление координат пункта Р_I

из треугольника l-ll-Р_I

Измеренные углы: r₁=71^°,r₂=56^°,g₁=53^°.

Исходные данные:

Х_I = 20 м; У_I = 50 м; Х_II = 220 м; У_II = 110 м; Х_III = 230 м; У_III = 290 м. (см. табл.2)

Решение.

Определяем дирекционные углы сторон:   

=

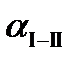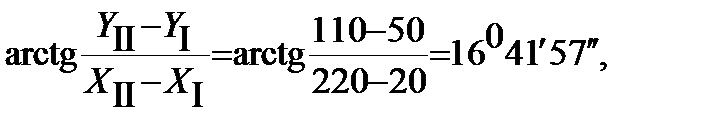
a _Р-I = a_I-II + b₁ = 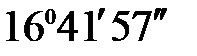 + 71° = .

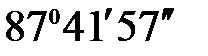a_{Р- II} = a_{I - II}  - b₂ + 180^º = 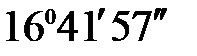 - 56^° + 180 ° = ;

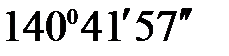Определяем углы при точке 1:

g₁ = 180^º - b₁ - b₂  = 180° - 71° -56° = 53°;

или  

g₁ = a_Р-II - a_Р-I = 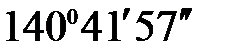- 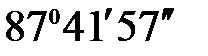= 53°.

Определяем координаты точки Р:

;

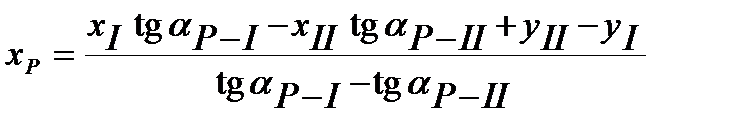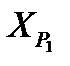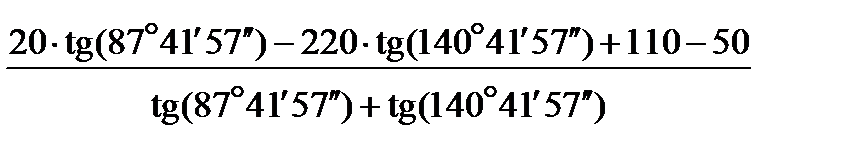= =28,702 м,

;

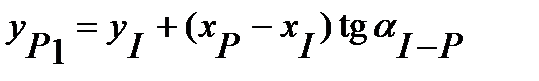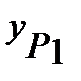 = 50 + (28,702 – 20) tg  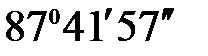= 266,582 м.

 

Вычисление координат пункта Р₁

из треугольника ll-lll-Р₁

Измеренные углы: r₃=54^°; r₄=80^°10´; g₂=46^°

Исходные данные:

Х_II = 220 м; У_II = 110 м; Х_III = 230 м; У_III = 290 м. (см. табл.2).

Решение.

Определяем дирекционные углы сторон:

=

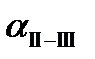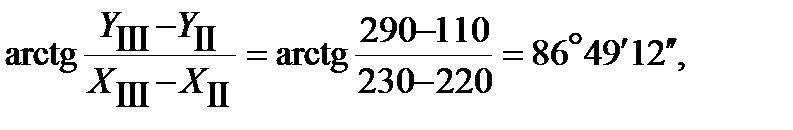
a _Р-II = a_II-III + b₁ = 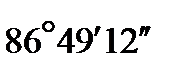 + 54° = ;

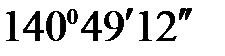a_{Р- III} = a_{I - III}  - b₂ + 180^º = 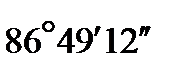 - 80^°05´ + 180 ° = .

 

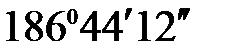Определяем углы при точке Р:      

 

g₁ = 180^º - b₁ - b₂  = 180° - 54° - 80°05´ = ,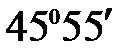

или  

g₁ = a_Р-III - a_Р-II = - = .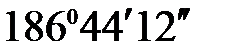

 

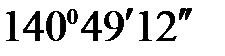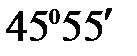Определяем координаты точки Р:

 

;

 

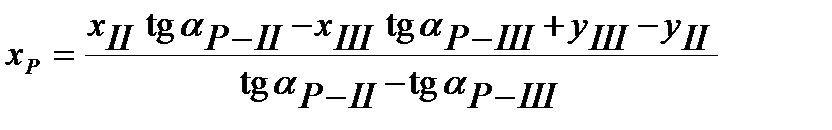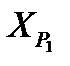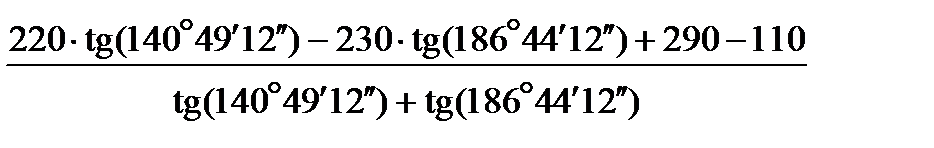= =28,368 м,

 

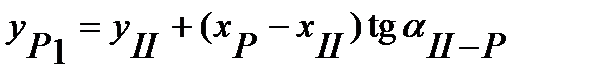
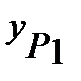= 110 + (28,368 – 220) tg  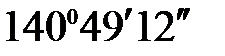= 266,180. 

Из решения двух  треугольников разница в координатах точки Р₁ составляет

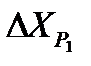 =-0,334 м,  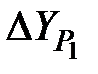   =-0,402 м,

 

которая не превышает 0,6 мм на плане в масштабе съемки (для масштаба 1:2000 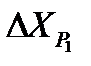, 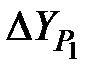£ 1,2 м).

    Среднеарифметическое значение координат точки Р₁ из двух треугольников:

 

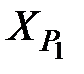 =28,535 м, 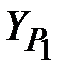=266,381 м.