Линейная засечка – способ определения координат точки съемочного обоснования по известным координатам двух пунктов опорных сетей и измеренным расстояниям от пунктов опорных сетей до определяемого (рис.6).
Наиболее известны два способа решения линейной засечки [2], где a и b – измеренные, с - исходная сторона треугольника; р – полусумма квадратов длин сторон
,
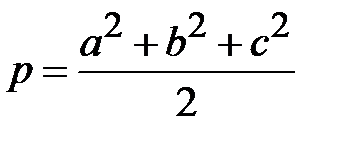и затем по определенным углам вычисляют координаты пункта Р1, решая прямую геодезическую засечку.
Длины a, b берутся с плана участка карьера, измеряются линейкой с точностью 0,5 мм в масштабе плана; с - исходная сторона, вычисляется решением обратной геодезической задачи по координатам пунктов опорных сетей (I, II) .
Первый способ.
Решают линейный треугольник (см. рис.6), определяя углы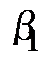 
и 
:
, 
,
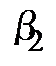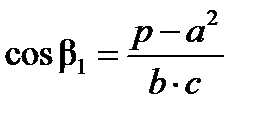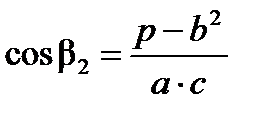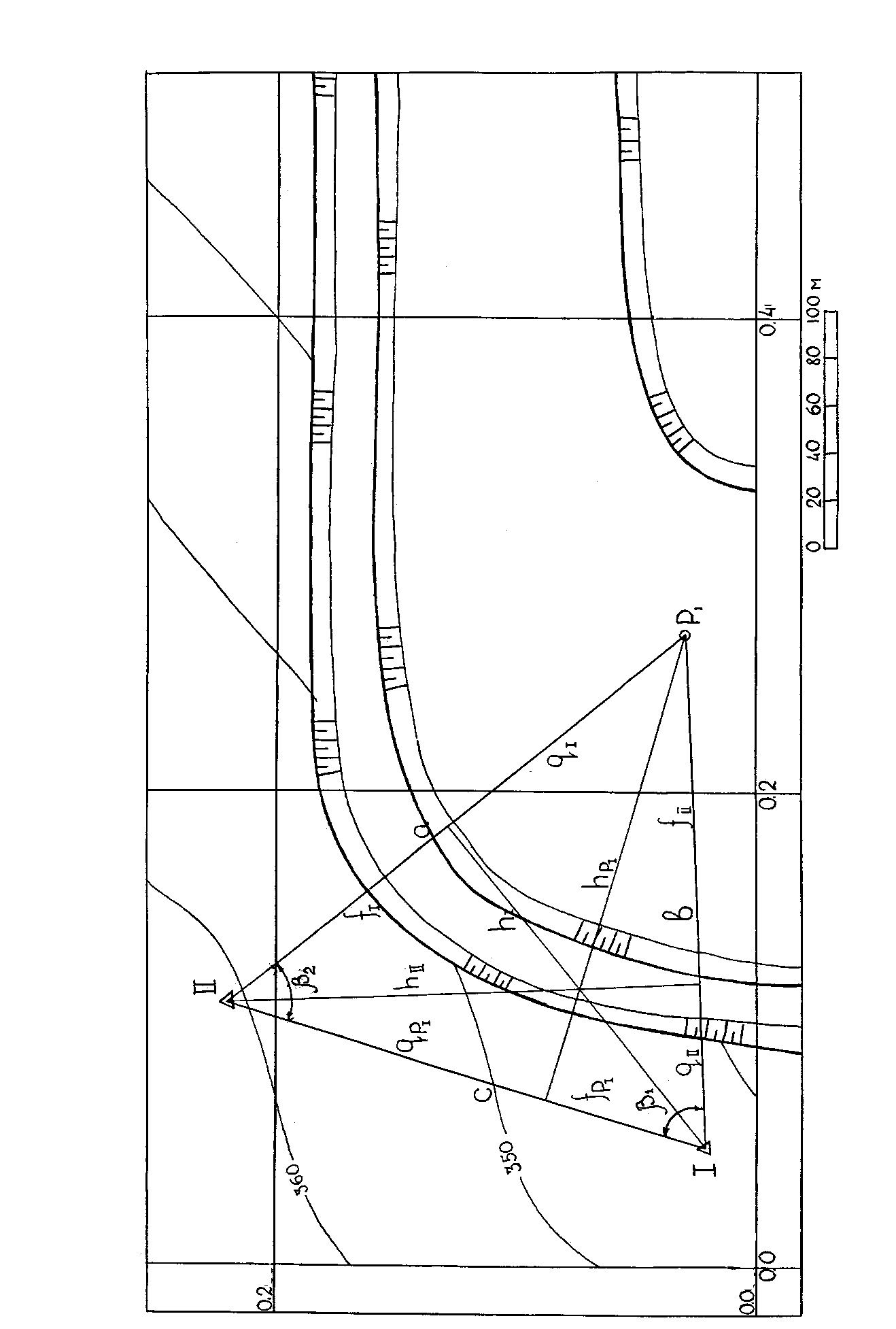
Второй способ - по проекциям измеренных сторон (см. рис. 6). Координаты пункта Р1 вычисляют исходя от пунктов опорных сетей:
от пункта I
= 
;
= 
;
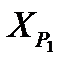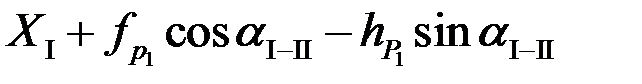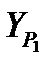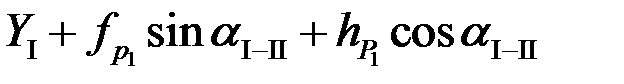от пункта II
= 
;
= 
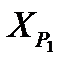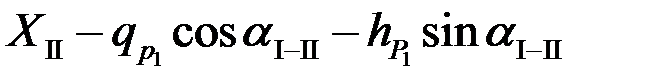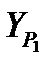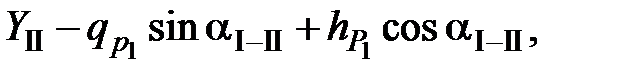
где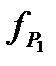 
и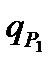 
- проекции двух сторон треугольника на третью сторону
;
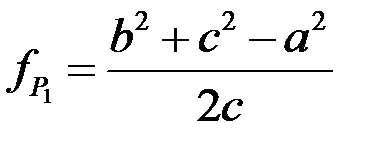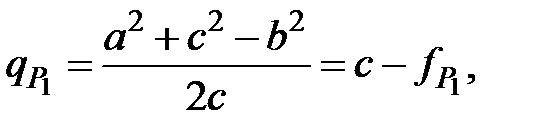
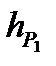- высота треугольника
= 
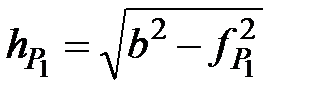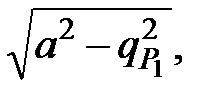
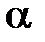- дирекционный угол исходной стороны
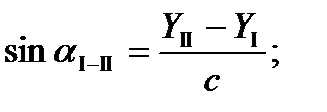
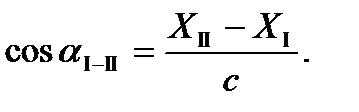
Высота треугольника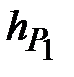 
принимается с соответствующим знаком: плюс, если точка Р1 расположена справа по отношению к линии I-II, и минус, если слева.
Контроль. Решается второй треугольник (см. рис.2) или в данном случае сравниваются полученные координаты с координатами из задачи 2. Допустимая разница в координатах 0,4 мм на плане в масштабе сьемки.
Методические указания для решения линейной засечки
1. На плане участка карьера строится один треугольник по схеме решения прямой геодезической засечки (см. рис. 2).
2. Измеряются два расстояния a и b от точки Р1 до опорных пунктов I и II с точностью до 0,5 мм в масштабе плана (на практике расстояния измеряются с точностью 1:3000).
3. Вычисляется сторона (с), решая обратную геодезическую задачу.
Исходные данные:
XI =20 м; YI =50 м;
XII =220 м; YII =110 м;
длины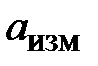 
=249,6 м; 
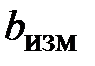=218,8 м.
Вычисляется: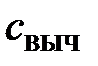 
=208,806 м.
Решение (первый способ):
,
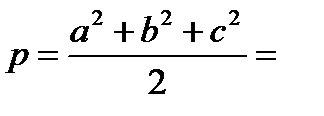
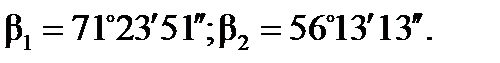
Решение прямой геодезической засечки
По формулам котангенсов измеренных углов
= 
=
= 
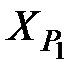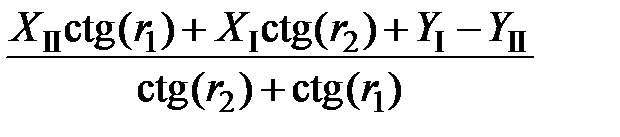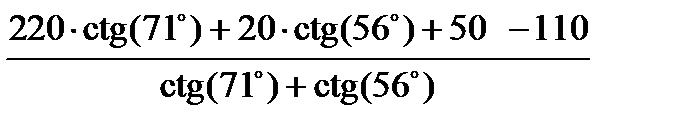= 28,634 м,
= 
=
= 
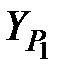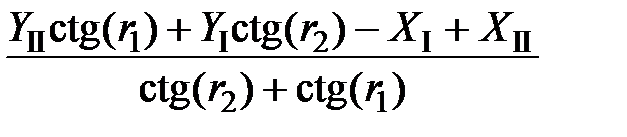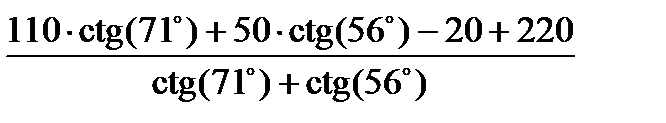= 266,739 м.
Контроль промежуточный:
XI =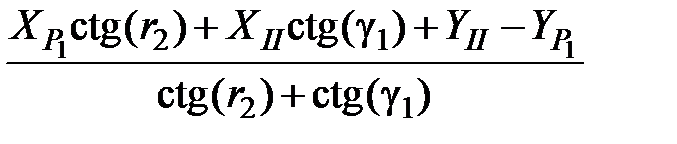 
=
= 
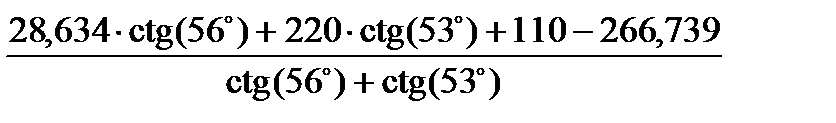=19,776 м.
YI =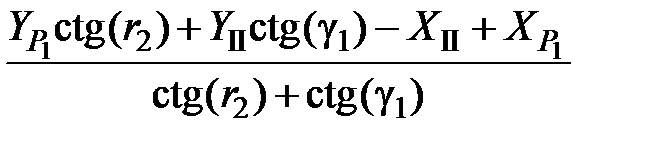 
=
= 
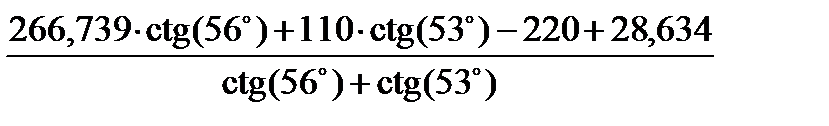= 49,927 м.
Контроль: решение второго треугольника.
Решение (второй способ):
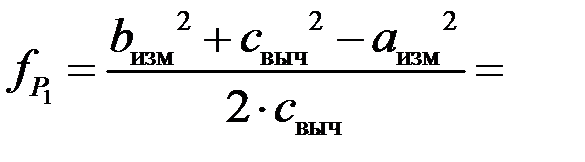
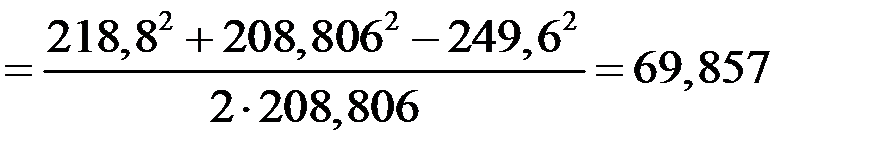м,
= 
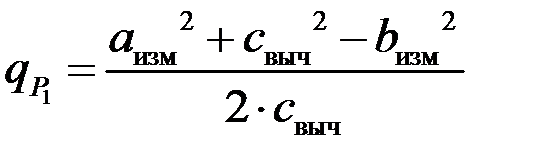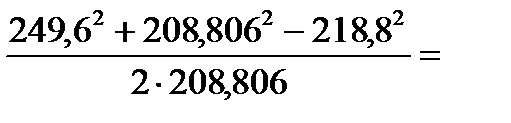138,949 м,
= 
- 
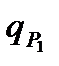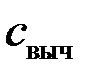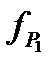= 208,806-69,857=138,949 м,
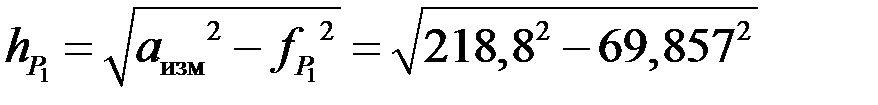=207,348 м,
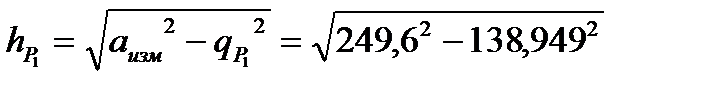=207,348 м,
,
.
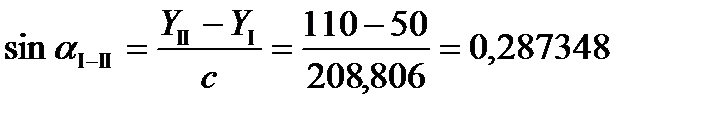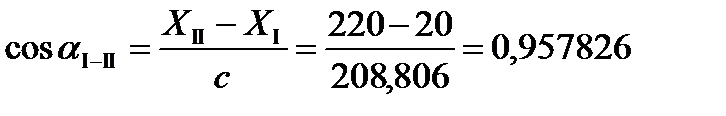От пункта I
,
.
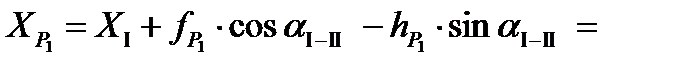
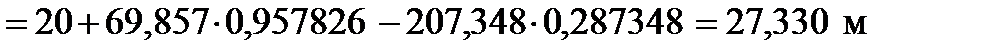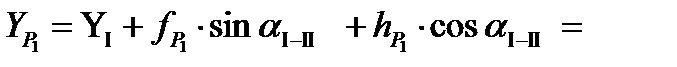
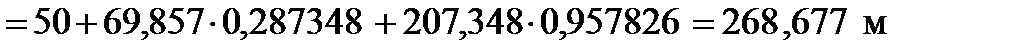От пункта II
,
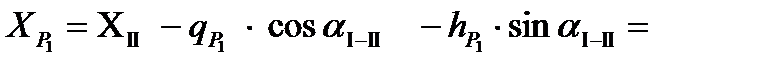
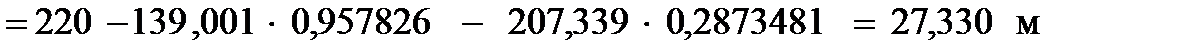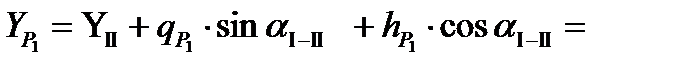
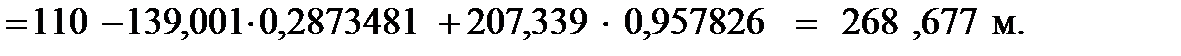
Контроль.
От пункта I:
, 
, 
.
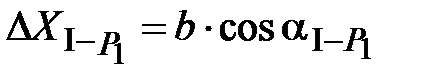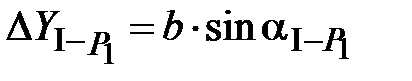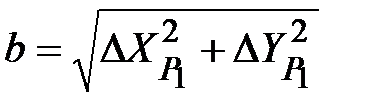От пункта II:
, 
, 
.
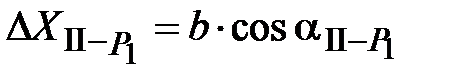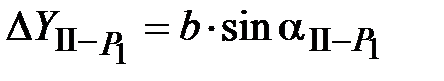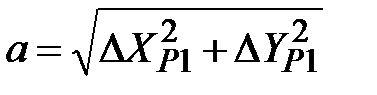где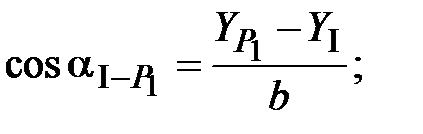 
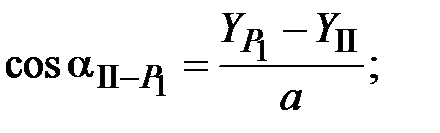
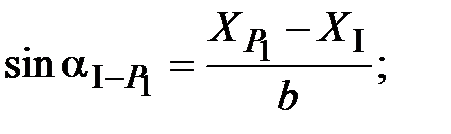
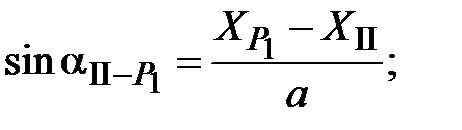
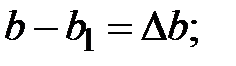
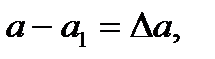
где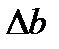 
и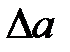 
- погрешность определения координат точки Р1 относительно пунктов опорной сети.
;
;
; 
;
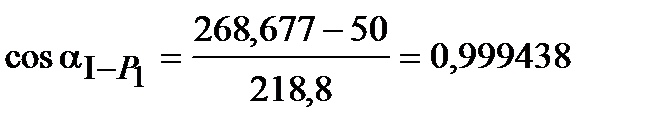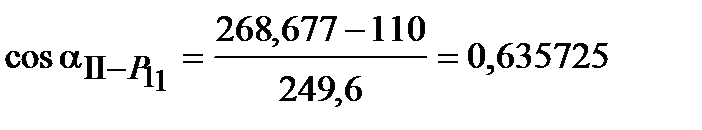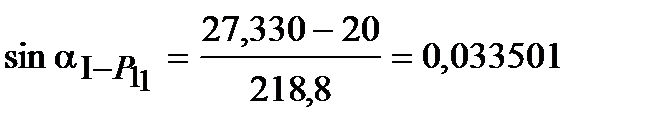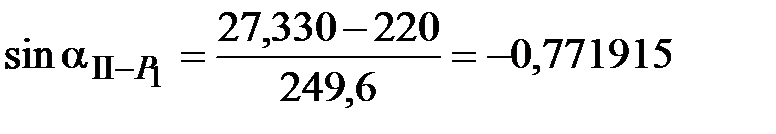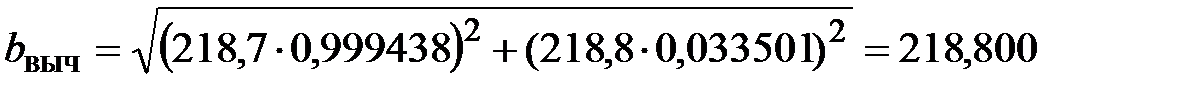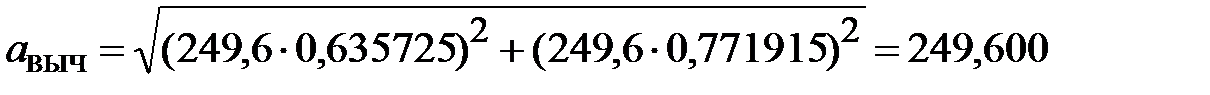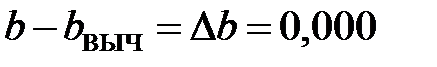м,
м,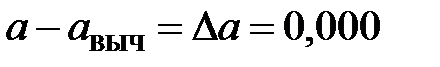
м, 
м.
По результатам расчетов ошибка определения точки Р1 относительно опорных сетей составила 0 мм при допустимой 0,4 мм на плане в масштабе съемки (0,8 м).
Для дополнительного контроля сравниваем полученные значения координат точки Р1, с координатами из решения первым способом или прямой засечки (см. задачу 2).
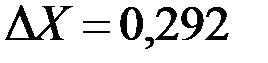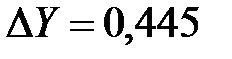м 
м.
Полученные разницы в координатах из двух способов решения не превышают допустимого расхождения 0,6 мм в масштабе съемки (для масштаба 1:2000 – 1,2 м.).
Принимаем среднее значение координат точки Р1
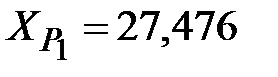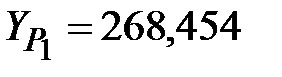м 
м.
Дата: 2018-11-18, просмотров: 469.
