Геодезические засечки - способ определения плановых координат (X, Y) отдельных пунктов по необходимому числу измеренных угловых и линейных величин. В зависимости от методики измерений и вычислений геодезические засечки называются: прямая, обратная, азимутальная, линейная.

    Расчет координат определяемого пункта ведется из двух треугольников в прямой и линейной и из двух вариантов в обратной засечке. За окончательные координаты принимается среднеарифметическое их значения. Допустимое расхождение в полученных координатах одного пункта  из двух решений не должно превышать 0,6 мм на плане в масштабе съемки. Наиболее выгодной формой треугольника, с точки зрения точности определения координат, является треугольник, в котором углы при определяемом пункте между направлениями на исходные не менее 30^о и не более 150^о. Расстояния между исходными пунктами и определяемым не должны превышать 1, 2, 3 км, соответственно в масштабах планов съемки 1:1000, 1:2000, 1:5000 [1].

  Таблица 2

Пример расчета координат точек теодолитного хода,  полигон № 1

Точки		Горизонтальные проложения, м	Горизонтальные углы		Дирекцион- ные углы °    ' "	Приращения, м		Координаты, м		Номер пункта	Эскиз
стоя- ния	наблю-дения		измеренные °    ' "	исправленные °    ' "		DY	DX	Y	X
I					75 55 55	-2 24136	6,048	6425 312,050	640 720,200	I	IIIII IV II V I
	II	24,882						336,184	726,248	II
II			+10 179 52 51	179 53 01	75 48 56	-2 26,093	6,595
	III	26,913						362,275	723,843	III
III			+9 4 29 12	4 29 21	260 18 17	-1 -17,028	-2,909
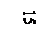
	IV	17,275						345,246	729,934	IV
IV			+9 175 53 38	175 53 47	256 12 04	-1 -15,581	-3,827
	V	16,044						329,664	726,107	V
V			+9 175 15 27	175 15 36	251 27 40	-1 -17,613	-5,907
	I	18,577						312,050	720,200	I
I			+9 4 28 06	4 28 15	75 55 55
	II
		P = 103,691	fb=–46"			fy=0,007	f х=0,000

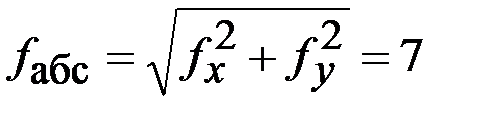 мм;          ;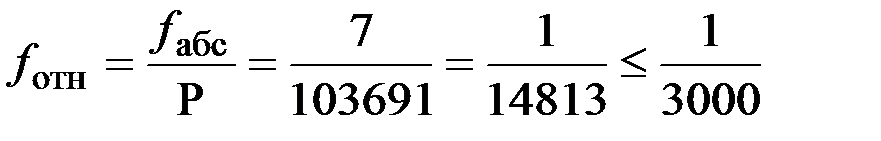     

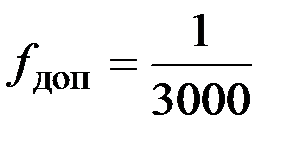
Продолжение таблицы 2

Пример расчета координат точек теодолитного хода, полигон № 2

Точки		Горизонтальные проложения, м	Горизонтальные углы		Дирекцион- ные углы °    ' "	Приращения		Координаты		Номер пункта	Эскиз
стоя- ния	наблю-дения		измеренные °    ' "	исправленные °    ' "		DY	DX	Y	X
VI					70 30 30	16,196	5,733	6125 350,04	640 710,100	VI	IIIX VII X VI VIII
	VII	17,182						366,238	715,833	VII
VII			+2 176 52 55	176 52 27	67 23 27	15,684	6,532
	VIII	16,99						381,923	722,365	VIII
VIII			+2 176 28 38	176 28 40	63 52 7	+1 15,409	+1 7,559
	IX	17,163						397,332	729,925	IX
IX			+2 4 5 26	4 5 28	247 57 35	+1 -24,944	-10,099
	X	26,913						372,387	719,826	X
X			+3 178 31 12	178 31 15	246 28 50	+1 -22,348	-9,726
	VI	24,372						350,040	710,100	VI
VI			+2 4 1 38	4 1 40	70 30 30
	VII
		P = 102,620	fb=-11"			fy=-0,003	fх=-0,001

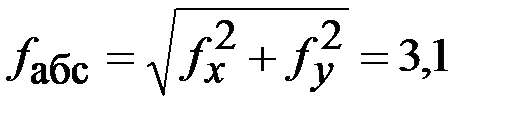 мм;  ;    .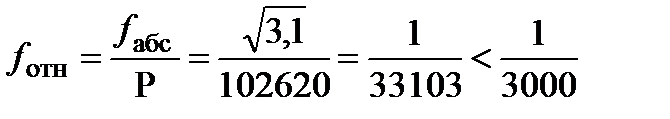

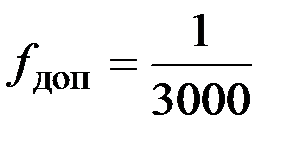Задача 2. Прямая геодезическая засечка

     Для решения прямой геодезической засечки на исходных пунктах I, II, III (рис. 2) измеряются углы r₁ и r₂ в одном треугольнике и r₃, r₄ во втором. Для определения координат пункта P₁ достаточно решения одного треугольника по известным координатам X_I, Y₁, X_II, Y_II пунктов I, II и измеренным углам r₁, r₂. Решение второго треугольника по известным координатам X_II, Y_1I, X_III, Y_III и измеренным углам r₃, r₄ проводится для контроля.

    Известны несколько способов решения прямой засечки. Наиболее распространенные из них два: по формулам котангенсов измеренных углов и тангенсов дирекционных углов [2].