Номинальный валютный (обменный) курс – это цена единицы национальной валюты, выраженной в единицах иностранной валюты. Термин «обменный курс валюты» используют для обозначения номинального курса.

Реальный валютный курс отражает реальное соотношение покупательной способности валют разных стран, т.е. соотношение величины потребительской корзины одной страны к потребительской корзине другой страны , приобретенных в каждой стране по номинальному курсу.

Реальный валютный курс отражает пропорции обмена, поэтому его считают условием торговли.

Зависимость между номинальным и реальным обменным курсом имеет вид (13.7):

                                                               (13.7)

Где E_r- реальный валютный курс;

E_n- номинальный валютный курс;

P_d- уровень (индекс) внутренних цен в национальной валюте;

P_f- уровень (индекс) цен за рубежом, выраженных в иностранной валюте.

В соответствии с формулой 11 реальный валютный курс зависит от трех параметров: номинального валютного курса, уровня цен в стране, уровня цен за рубежом.

Валютный курс: виды, факторы влияния. Воздействие изменений валютного курса на торговый баланс. Условие А.Маршалла-А.Лернера (формула Дж. Робинсон)

Вопрос по поводу эффекта (отрицательного или положительного) влияния изменения валютного курса на стабильность платежного баланса долгое время игнорировался в экономической теории. Без сомнений преобладало мнение, что колебания валютного ресурса оказывают благоприятные воздействия на баланс текущих платежей. Возможность «извращенного эффекта», по выражению Л.Метцлера, не рассматривалась. А.Маршалл в работе «Валюта, кредит и торговля» первым указал на то, девальвация может иметь и негативные последствия для уравновешенного торгового баланса, если общая эластичность спроса каждой страны ниже 1 и если в среднем она меньше ½.

Идея А.Маршалла положена в основу исследования Дж.Робинсон по поводу неоднозначных последствий девальвации валюты для торгового баланса.

В анализе ею были использованы четыре вида эластичности:

а) со стороны экспорта:

· эластичность экспортного спроса от заграницы;

· эластичность национального экспортного предложения.

б) со стороны импорта:

· эластичность импортного предложения от заграницы;

· эластичность национального импортного спроса.

Проследив влияние девальвации по эластичности на стоимость экспорта и импорта Дж.Робинсон в математической форме выявила следующие зависимости:

1. Влияние девальвации на стоимость экспорта будет максимальным, если зарубежный спрос и национальное экспортное предложение будут полностью эластичны. Оно будет минимальным, если зарубежный спрос будет неэластичен.

2. В результате девальвации валют стоимость импорта возрастет тем больше, чем менее эластичным будет национальный импортный спрос. Оно сократится тем больше, чем более эластичными будут национальный импортный спрос и зарубежное импортное предложение .

Конечным результатом экономико-математического исследования является формула Дж.Робинсон (выведенная также и А.Лернером). если первоначально имеем уравновешенный торговый баланс и неограниченную эластичность предложений, то увеличение баланса выражается следующей формулой (13.8):

K*Eq(ef+eh-1)                                                                                           (13.8)

где K – снижение валютного курса в процентах,

Е- экспорт,

q – цена экспорта в национальной валюте;

ef – эластичность зарубежного экспортного спроса;

eh – эластичность национального импортного спроса.

Формула (13.8) указывает на то, что в результате снижения валютного курса торговый баланс может улучшиться, если сумма эластичностей национального и зарубежного превысит 1. если сумма эластичностей будет равна 1, никакого улучшения баланса не произойдет. Имеет место ухудшение баланса, если сумма эластичностей будет меньше 1.

Формула Дж.Робинсон (выведенная и А.Лернером) получила название «условие Маршалла-Лернера».

Отметим что формула (13.8) действенна при первоначальном равновесии экспорта и импорта. Формула выявляет последствия девальвации, но на доказывает, насколько следует девальвировать, чтобы скорректировать дефицит платежного баланса. Эта проблема была решена в последующих разработках. В частности, А. Дэй представил формулу (13.9):

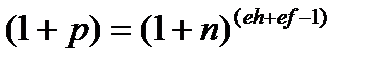                                                  (13.9)

где n - процент девальвации, необходимый для восстановления баланса;

p – начальный дефицит баланса, рассчитанный в процентах дохода в иностранной валюте.

Преимущество формулы (13.9) в том, что она является указанием для реальных действий.